Лабораторная работа 1.1
В любой физической лаборатории всегда присутствует радиоактивное излучение. Источником излучения являются космические лучи и распад радиоактивных веществ, которые в небольших количествах имеются всюду, в том числе в физических приборах и в помещениях. Это излучение является радиоактивным фоном, с которым складывается излучение других источников, если они присутствуют.
В данной работе для измерения уровня фонового излучения используется дозиметр ДБГ-06Т. Дозиметр предназначен для измерения мощности экспозиционной дозы на рабочих местах. Время измерения в режиме работы «Измерение» составляет около 40 секунд.
В данном дозиметре для регистрации ионизирующих частиц используется счетчик Гейгера-Мюллера.
При любом физическом измерении результат, получаемый на опыте, несколько отличается от действительного значения измеряемой величины. Погрешность измерений складывается из ошибок, связанных с несовершенством методики измерений и неточностью калибровки приборов (эти ошибки принято называть систематическими), и из случайных ошибок эксперимента, изменяющих свою величину и знак от опыта к опыту. Частным случаем случайных ошибок являются так называемые статистические ошибки. Эти ошибки вызываются флуктуациями (случайными отклонениями) самой измеряемой величины.
К числу флуктуирующих величин относится и мощность экспозиционной дозы излучения. Пусть при некотором измерении за сорок секунд зарегистрирована экспозиционная доза 
миллирентген в час (по показаниям прибора). Из этого отнюдь не следует, что в любые следующие сорок секунд будет регистрироваться именно 
миллирентген в час. В силу случайных причин при этом можно получитьлюбое другое, вообще говоря, не слишком сильно отличающееся от значение.
В этом случае, как и всегда при измерении флуктуирующих величин, физический смысл имеет не столько результат отдельного измерения, сколько средний результат опыта, в нашем примере – среднее количество миллирентген в час, измеряемых дозиметром.
Чтобы определить среднюю экспозиционную дозу, следует несколько раз измерить мощность экспозиционной дозы, результаты просуммировать и разделить полученное число на количество измерений. Строго говоря, средняя мощность равна пределу, к которому стремятся получаемые таким образом числа при беспредельном увеличении количества измерений.
Отдельные измерения, проведенные в течение некоторого времени, позволяют определить искомую среднюю мощность экспозиционной дозы излучения не вполне точно, а с некоторой ошибкой, величина которой тем меньше, чем больше число измерений.
Рассмотрим более внимательно опыт по определению мощности экспозиционной дозы излучения. При небольших размерах установки и не очень большом времени, которое можно использовать для опыта, все ошибки оказываются пренебрежимо малыми по сравнению со статистическими флуктуациями, поэтому никаких других отклонений, кроме статистических, мы рассматривать не будем. Проведем ряд опытов по измерению мощности экспозиционной дозы излучения. Сравнив полученные результаты, мы увидим, что найденные значения заметно отличаются друг от друга, хотя среди них встречаются и одинаковые.
Построим график, откладывая по оси абсцисс мощность экспозиционной дозы излучения, зарегистрированную при измерениях, а по оси ординат - долю случаев (по отношению к общему числу измерений), в которых было зафиксирована данная мощность.
Построенный график содержит дискретно расположенные точки, которые для наглядности обычно соединяются между собой. Лучше всего это делать, представляя график в виде совокупности вертикально стоящих прямоугольников, как это изображено на рис. 1
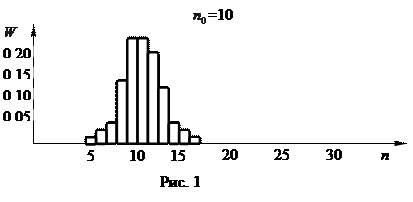
На этом графике прямоугольник, расположенный между 0 и 1, характеризует случаи, в которых регистрировались значения от 0 до 1 мкР/ч (микрорентген в час, включая 0 и не включая 1); прямоугольник, расположенный между 1 и 2 - значения от 1 до 2 мкР/ч и т.д. Высота прямоугольника определяет долю наблюдаемых случаев 
. Подобного рода график принято называть гистограммой.
Мы получим, таким образом, график распределения результатов опыта, который обнаруживает максимум в области искомого среднего значения, хотя среди результатов попадутся и такие, которые сильно отличаются от среднего. Доля случаев, в которых происходит некоторое событие (например, обнаруживается данное значение), называется вероятностью этого события.
Построенный график (гистограмма), таким образом, характеризует распределение вероятности зарегистрировать мощность экспозиционной дозы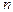 
мкР/ч в зависимости от величины 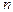. Обозначим среднюю (вообще говоря, нам неизвестную) мощность излучения 
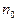мкР/ч.
В самом деле, многократные измерения производятся редко. Наибольший интерес представляет ожидаемое отличие результата, полученного при одиночном измерении, от истинного значения. При однократном измерении отклонение результата от истинного в зависимости от случая может быть большим или меньшим, но чаще всего оно по порядку величины равно полуширине кривой распределения (1/2 ширины гистограммы на уровне половины высоты), а полуширина характеризует поэтому точность однократного измерения.
Для оценки точности измерений обычно применяют величину, называемую дисперсией. Дисперсией 
случайной величины называется среднее значение квадрата отклонения этой величины от ее среднего значения:
Сама величина 
(корень квадратный из дисперсии) называется среднеквадратичной ошибкой или стандартным отклонением.
В теории вероятностей показывается, что чаще всего для экспериментов в 68 случаях из 100 (т.е. с вероятностью 68%) истинное среднее значение отличается от результатов измерения не более чем на одну среднеквадратичную ошибку (
); с вероятностью 95% - не более чем на две среднеквадратичные ошибки (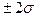
) и с вероятностью 99,7% - не более чем на три среднеквадратичные ошибки (
).
Поскольку показания дозиметра пропорциональны количеству частиц, попавших на счетчик Гейгера, то из теории следует также, что среднеквадратичная ошибка единичного измерения пропорциональна корню от числа частиц и, следовательно, корню из значения мощности экспозиционной дозы: 
.
Обратимся теперь к следующему важному вопросу. Пусть мы провели серию из N измерений, в результате которой получены значения мощности n1, n2,..., nN . Эти результаты мы до сих пор использовали для того, чтобы определить, как отличаются друг от друга значения, полученные в разных измерениях. Как уже отмечалось, этот вопрос важен главным образом для выяснения того, насколько достоверен результат, полученный в одном измерении. Но если было проведено несколько измерений, их результаты могут быть использованы и с другой целью: они позволяют определить среднее значение измеряемой величины точнее, чем это можно сделать, если произведено всего одно измерение. При N измерениях среднее значение мощности экспозиционной дозы излучения равно, очевидно,
, (1)
а стандартная ошибка отдельного измерения, по определению, равна
, (2)
Величина 
из формулы (1), полученная путем усреднения результатов по серии из N опытов, конечно, тоже не вполне точно совпадает с истинным средним значением 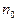, и сама является случайной величиной, но отклонение величины 
от 
, вообще говоря, существенно меньше, чем 
.
Теория вероятностей показывает, что стандартная ошибка отклонения 
от может быть определена по формуле:
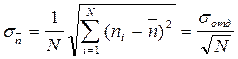, (3)
Обычно наибольший интерес представляет не абсолютная, а относительная точность измерений. Для рассмотренной серии из N измерений относительная ошибка отдельного измерения (т.е. ожидаемое отличие любого из 
от ) равна
.
Аналогичным образом относительная ошибка в определении среднего по всем измерениям значения равна
. (4)
Таким образом, относительная точность измерения определяется полным числом значений 
. Этого, конечно, и следовало ожидать, так как все измерения вместе составляют одно более продолжительное измерение. Как мы видим, относительная точность измерения постепенно улучшается с увеличением числа экспериментов.
Измерения:
Ознакомьтесь с устройством дозиметра ДБГ-06Т.
Включите дозиметр, для чего установите левый верхний переключатель диапазонов в положение мР/ч., а правый верхний переключатель режимов работы в положение КОНТР.
Осуществите сброс показаний нажатием кнопки СБРОС. На цифровом табло при правильном функционировании счетных устройств дозиметра и пригодности источника питания должно устойчиво отображаться число 0515 (без учета запятых). Прибор готов к работе.
Установите правый верхний переключатель режимов работы в положение ИЗМЕР.
Произведите сброс показаний нажатием кнопки СБРОС.
В режиме работы «Измерение» на цифровом табло отображаются нули во всех разрядах, и мигает запятая в младшем разряде. Отсчет показаний производится в конце цикла измерения (через 40 сек.) в момент прекращения мигания запятой младшего разряда. Показания на цифровом табло сохраняются до момента нажатия кнопки СБРОС. Нажатие кнопки СБРОС одновременно запускает дозиметр на новый цикл измерения.
Запишите показания дозиметра в таблицу результатов.
Проведите N = 100 измерений мощности экспозиционной дозы излучения. Результаты опыта представьте в виде гистограммы 
. Для этого по оси абсцисс отложите последовательные значения n, а по оси ординат - долю случаев, когда показание дозиметра равнялось n. Доля случаев , характеризующая вероятность получить значение n, определяется по очевидной формуле:
(число случаев с отсчетом n) / (полное число измерений N).
Определите 
-среднюю мощность экспозиционной дозы излучения (по формуле (1)) и 
- среднеквадратичную ошибку отдельного измерения по формуле (2).
Отметьте на гистограмме среднее значение мощности экспозиционной дозы 
, а также значения 
.
Измерьте по гистограмме полуширину распределения, т.е. 1/2 ширины гистограммы на уровне половины высоты. Сравните полученное значение с величиной 
.
Определите долю случаев, когда отклонения от среднего значения превышают 
, 2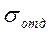 
, по формуле:
W=(число случаев, когда отклонение от среднего значения превышает (2 
)) / (полное число измерений N).
Сравните найденную из опыта долю таких случаев с теоретическими оценками. При сравнении теоретических оценок с экспериментальными данными следует помнить, что при конечном, а тем более при небольшом числе опытов, точного согласия между ними быть не может. Экспериментальные данные содержат в себе элемент случайности, которого нет в теоретических оценках. Согласия экспериментальных результатов с теоретическими оценками следует ожидать лишь по порядку величины.
Определите стандартное отклонение величины 
, используя всю совокупность измерений (по формуле (3)). Найдите относительную ошибку этого результата по первому равенству (4).
Отметьте на гистограмме значения 
Обменяйтесь результатами измерений с тремя другими подгруппами. Постройте сводную гистограмму для 400 измерений. Рассчитайте среднее значение мощности экспозиционной дозы и его стандартное отклонение в этом случае. По гистограмме оцените среднеквадратичную ошибку отдельного измерения. Сделайте вывод.
Оформите отчет о проделанной работе.
Лабораторная работа 1.2
