25 вариантов контрольной работы, разработанные по данному теоретическому материалу. Один вариант контрольной работы включает в себя 10 заданий. При решении некоторых заданий рекомендуется сделать чертеж, что упростит ход действий при ее решении. Все задачи подобранны таким образом, что каждый учащийся который ознакомлен с теорией разобранной в данной курсовой работе сможет дать ответы на задания. Данный комплекс упражнений поможет выявить уровень знаний по данной теме.
Вариант 1.
Задание №1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(2;4;3), А2(7;6;3), А3(4;9;3), А4(3;6;7). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание №2.
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB= 2, ребро AD= 
, ребро АА1=2. Точка К - середина ребра ВВ1. Найдите площадь сечения, проходящего через точки A1,D1 и К.
Задание№3.
Даны координаты вершин параллелепипеда:A(3;4;4), B(5;1;3), C(2;2;3), D(1;1;5). Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
Задание №4.
Проверить, лежат ли в одной плоскости точки A(-2;-13;3), B(1;4;1), C(-1;-1;-4), D(0;0;0). Найти линейную зависимость вектора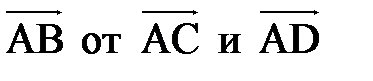 
, если это возможно.
Задание №5.
Докажите, что если точки пересечения медиан треугольников ABC и А1В1С1 совпадают, то прямые АА1, ВВ1 и СС1 параллельны некоторой плоскости.
Задание №6.
Ребро куба АBCDA1B1C1D1 равно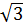 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю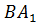 
грани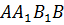 
и плоскостью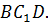 
Задание №7.
Найдите расстояние между скрещивающимися диагоналями АВ1 и ВС1 смежных граней АА1ВВ1 и ВВ1СС1 куба ABCDA1B1C1D1, если ребро этого куба равно 6.
Задание№8.
В кубе ABCDA1B1C1D1 со стороной a точка K является серединой стороны верхнего основания B1C1, точка L делит другую сторону C1D1 этого основания в отношении 2:1, считая от вершины С1, точка N является серединой бокового ребра АА1. Найдите площадь сечения, проходящего через точки К, L, N.
Задание№9.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AB и CA1.
Задание №10.
В правильной прямоугольной призме ABCA 1 B 1 C 1все ребра которой равны 1, найдите квадрат косинуса угла между прямыми АВ и А1С.
Вариант 2.
Задание №1.
Даны координаты вершин пирамиды А1А2А3А4:
A1(1;8;2),A2(5;2;6), A3(0;-1;-2), A4(-2;3;-1). Найти:
1) длину ребра А1А2;
2) угол между ребрами А1А2 и А1А4;
3) угол между ребром А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3;
5) объем пирамиды.
Задание №2.
Диагональ основания правильной четырехугольной призмы равна 5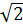 
, а диагональ призмы наклонена к плоскости основания под углом 60°. Найдите площадь сечения призы, проходящего через сторону нижнего основания и противоположную сторону верхнего основания.
Задание №3.
Даны координаты вершин параллелепипеда: A(1;8;2), В(5;2;6), С(0;-1;-2), D(-2;3;-1). Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
Задание №4.
Проверить, лежат ли в одной плоскости точки А(4;4;2), В(3;-3;4), С(2;3;-3), D(3;-4; 5). Найти линейную зависимость вектора 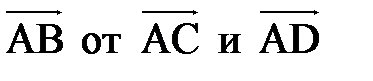, если это возможно.
Задание №5.
На двух скрещивающихся прямых отмечены по три точки: A1, A2, A3 и B1, B2, B3, причем A1A2=k⋅A1A3, В1В2= k⋅В1В3. Докажите, что прямые А1В1, А2В2, A3B3 параллельны некоторой плоскости.
Задание№6.
В кубе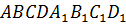 
, ребро которого равно 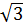, найдите:
а) расстояние от вершины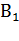 
до плоскости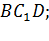 
б) угол между диагональю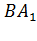 
грани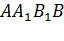 
и плоскостью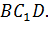 
Задание №7.
Дан куб ABCDA1B1C1D1 с длиной ребра AB= 
. Найдите расстояние между скрещивающимися диагоналями AC и А1В смежных граней ABCD и AA1B1B.
Задание №8.
В правильной треугольной пирамиде SАВС с вершиной S высота равна 3, а боковые ребра равны 6. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон АВ и АС параллельно прямой SА.
Задание №9.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1.
Задание №10.
В правильной четырехугольной пирамиде SABCD с вершиной S высота равна диагонали основания. Точка F лежит на середине ребра SВ. Найдите квадрат тангенса между прямыми SD и АF.
Вариант №3.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(4;3;4), А2(5;5;3), А3(6;8;0), А4(4;5;8). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник АВС. Середина D гипотенузы этого треугольника является основанием высоты SD данной пирамиды. Известно, что SD=2, AC=4, BC=3. Через середину высоты SD проведено сечение пирамиды плоскостью, параллельной ребрам AC и SB. Найти площадь этого сечения.
Задание№3.
Даны три вершины параллелограмма A(3;-2;4), B(4;0;3), C(7;1;5). Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание №4.
Проверить, лежат ли в одной плоскости точки А(1;2;3), В(3;-2;1), С(1;1;-3), D(5;-4; 5). Найти линейную зависимость вектора 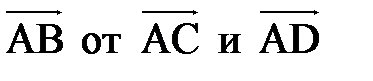, если это возможно.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно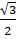 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 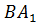грани 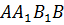и плоскостью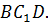
Задание№7.
Основание пирамиды – прямоугольник со сторонами 6 и 8. Одно из боковых рёбер перпендикулярно плоскости основания и равно 6. Найдите расстояние между этим ребром и скрещивающейся с ним диагональю основания, а также боковую поверхность пирамиды.
Задание №8.
На ребре МВ правильной пирамиды МАВС взяты точка К – середина этого ребра и точка L – середина отрезка ВК. Постройте сечение пирамиды плоскостью, проходящей через точку L параллельно прямым КА и МС. Найдите площадь полученного сечения, если сторона основания равна 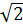, а боковое ребро равно 2.
Задание №9.
В основании прямой призмы ABCDA1B1C1D1 лежит ромб ABCD со сторонойи углом А, равным 60°. На ребрах AB, B1C1 и DC взяты соответственно точки E, F и K так, что AE=EB, B1F=FC1 и DK=3KC. Найдите косинус угла между плоскостями EFK и ABC, если высота призмы равна 5.
Задание№10.
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые ребра равны 5. На ребре AA1 отмечена точка E так, что AE:EA1=2:3. Найдите угол между плоскостями ABC и BED1.
Вариант №4.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(0;-1;1), А2(6;-4;-5), А3(9;-3;-1), А4(1;1;3). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В параллелограмме ABCD даны векторы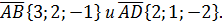 
Найти площадь параллелограмма, построенного на диагоналях параллелограмма ABCD.
Задание№3.
Даны три вершины параллелограмма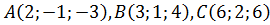 
. Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание№4.
Проверить, лежат ли в одной плоскости точки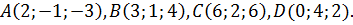 
Найти линейную зависимость вектора 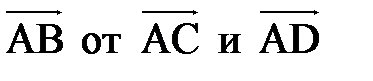, если это возможно.
Задание№5.
Докажите, что через данную точку можно провести плоскость, параллельную двум данным скрещивающимся прямым, и притом только одну.
Задание №6.
Ребро куба АBCDA1B1C1D1 равно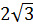 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
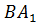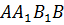б) угол между диагональю грани и плоскостью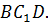
Задание№7.
Найдите угол между скрещивающимися медианами двух граней правильного тетраэдра.
Задание№8.
В прямоугольном параллелепипеде ABCDA1B1C1D1, AB=BC=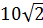 
, AA1=2 
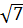. Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол 
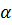=arctg 
. Найдите площадь сечения.
Задание№9.
Диаметр АС основания конуса равен образующей РА этого конуса. Хорда основания ВС составляет угол 600. Найдите косинус угла между прямыми АР и ВС.
Задание№10.
В правильной четырехугольной призме ABСDA1B1C1D1 стороны основания равны 2, а боковые ребра равны 5. На ребре АА1 отмечена точка Е так, что АЕ:ЕА1 = 3:2. Найдите угол между плоскостями АВС и ВЕD1.
Вариант№5.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(-5;1;3), А2(1;-2;-3), А3(4;-1;1), А4(-4;3;5). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB= 8, ребро AD=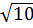 
, ребро АА1=4. Точка К - середина ребра ВВ1. Найдите площадь сечения, проходящего через точки A1,D1 и К.
Задание№3.
Точки A(-2;1;-3), B(3;4;4), C(5;6;0), E(4;6;t) служат вершинами параллелепипеда, объем которого равен 16. Найти t.
Задание№4.
Проверить, лежат ли в одной плоскости точки А(-5;1;3), B(1;-2;-3), C(4;-1;1), D(-4;3;5) Найти линейную зависимость вектора 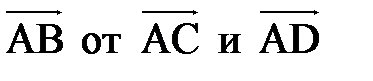, если это возможно.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах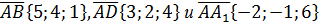 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 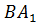грани 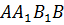и плоскостью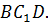
Задание№7.
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что СЕ:ЕС1=1:2. Найдите угол между прямыми ВЕ и АС1.
Задание№8.
В правильной треугольной пирамиде МАВС с вершиной М высота равна 3, а боковые ребра равны 6. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон АВ и АС параллельно прямой МА.
Задание№9.
В правильной четырехугольной пирамиде АВСMT со стороной основания АВ=4 и высотой ТО1=1. Найдите косинус угла между прямыми ОТ и MK, где О и К - середины ребер АВ и ТС.
Задание№10.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D середина ребра A1B1. Найдите тангенс угла между прямыми AD и BC1.
Вариант№6.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(-1;-3;0), А2(5;-6;-6), А3(8;-5;-2), А4(0;-1;2). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 6, а боковые рёбра равны 16. Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
Задание№3.
Проверить, лежат ли точки A(2;-2;2), B(1;2;1), C(2;3;0), D(5;0;-6) в одной плоскости.
Задание№4.
Точки A(-3;2;-3), B(4;4;4), C(6;6;1), E(5;4;t) служат вершинами параллелепипеда, объем которого равен 36. Найти t.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах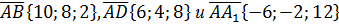 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно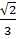 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 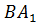грани 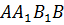и плоскостью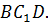
Задание№7.
В прямоугольном параллелепипеде ABCDA1B1C1D1,AB = 2, AD=AA1=1. Найдите угол между прямой АВ1 и плоскостью АВС1.
Задание №8.
Точка Е - середина ребра АА1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью C1DE, если ребра куба равны .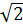
Задание№9.
В правильной четырехугольной пирамиде ABCDS с вершиной S боковое ребро АS вдвое больше стороны основания АВ. Найдите угол между прямыми AS и BK, где К – точка пересечения медиан грани СDS.
Задание №10.
Длины всех ребер правильной четырехугольной пирамиды SABCD равны между собой. Найдите угол между прямыми SН и ВМ, если отрезок SН - высота пирамиды, точка М - середина ее бокового ребра АS.
Вариант 7.
Задание №1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(-3;-2;-1), А2(3;-5;-7), А3(6;-4;-3), А4(-2;0;1). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB= 4, ребро AD= 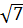, ребро АА1=6. Точка К- середина ребра ВВ1. Найдите площадь сечения, проходящего через точки A1,D1 и К.
Задание№3.
Даны три вершины параллелограмма А(-3;-2;-1), B(3;-5;-7), C(6;-4;-3). Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание№4.
Точки А(-3;-2;-1), В(3;-5;-7), С(6;-4;-3), D(-2;t;1) служат вершинами параллелепипеда, объем которого равен 64. Найти t.
Задание№5.
Докажите, что если точки пересечения медиан треугольников ABC и А1В1С1 совпадают, то прямые АА1, ВВ1 и СС1 параллельны некоторой плоскости.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно . Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 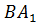грани 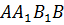и плоскостью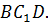
Задание№7.
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что СЕ:ЕС1=1:3. Найдите угол между прямыми ВЕ и АС1.
Задание№8.
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=BC=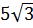 
, AA1=2 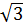. Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол 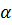=arctg 
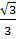. Найдите площадь сечения.
Задание№9.
Найдите площадь сечения правильной четырехугольной пирамиды SАВСD плоскостью, параллельной апофеме SL боковой грани SВС и медиане АМ боковой грани SАВ и проходящей через середину бокового ребра SC, если сторона основания пирамиды равна 8, а расстояние от вершины пирамиды до секущей плоскости равно 40/21.
Задание№10.
В кубе ABCDA1B1C1D1 точки E и K середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Вариант№9.
Задание №1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(-1;-4;-4), А2(12;-1;-13), А3(6;-6;-7), А4(-16;1;1). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание №2.
Диагональ основания правильной четырехугольной призмы равна 3 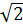, а диагональ призмы наклонена к плоскости основания под углом 30°. Найдите площадь сечения призы, проходящего через сторону нижнего основания и противоположную сторону верхнего основания.
Задание№3.
Даны координаты вершин параллелепипеда: A(-1;-4;-4), B(12;-1;-13), C(6;-6;-7), D(-16;1;1). Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
Задание №4.
Проверить, лежат ли в одной плоскости точки A(2;6;2), B(0;1;3), C(3;0;3), D(4;4;5). Найти линейную зависимость вектора 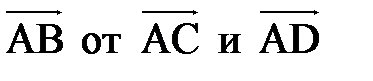, если это возможно.
Задание №5.
Докажите, что если точки пересечения медиан треугольников ABC и А1В1С1 совпадают, то прямые АА1, ВВ1 и СС1 параллельны некоторой плоскости.
Задание №6.
Ребро куба АBCDA1B1C1D1 равно 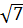. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 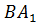грани 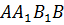и плоскостью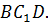
Задание №7.
Найдите расстояние между скрещивающимися диагоналями АВ1 и ВС1 смежных граней АА1В1В и ВВ1С1С куба ABCDA1B1C1D1, если ребро этого куба равно .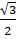
Задание №8.
В кубе ABCDA1B1C1D1 со стороной a точка K является серединой стороны верхнего основания B1C1, точка L делит другую сторону C1D1 этого основания в отношении 3:2, считая от вершины С1, точка N является серединой бокового ребра АА1. Найдите площадь сечения, проходящего через точки К, L, N.
Задание№9.
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны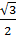 
, найдите косинус угла между прямыми AB и CA 1.
Задание №10.
В правильной прямоугольной призме ABCA 1 B 1 C 1все ребра которой равны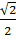 
найдите квадрат косинуса угла между прямыми АВ и А1С.
Вариант№10.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(2;2;5), А2(5;6;4), А3(3;2;2), А4(4;0;2). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник АВС. Середина D гипотенузы этого треугольника является основанием высоты SD данной пирамиды. Известно, что SD=4, AC=6, BC=7. Через середину высоты SD проведено сечение пирамиды плоскостью, параллельной ребрам AC и SB. Найти площадь этого сечения.
Задание№3.
Даны три вершины параллелограммаA(4;4;3), B(6;2;0), C(7;0;8). Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание №4.
Проверить, лежат ли в одной плоскости точки А(2;4;5), В(5;0;1), С(2;2;-1), D(5;-4; 5). Найти линейную зависимость вектора 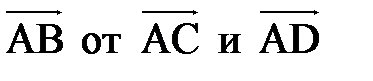, если это возможно.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах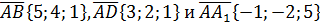 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно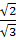 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 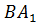грани 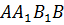и плоскостью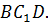
Задание№7.
Основание пирамиды – прямоугольник со сторонами 12 и 18. Одно из боковых рёбер перпендикулярно плоскости основания и равно 4. Найдите расстояние между этим ребром и скрещивающейся с ним диагональю основания, а также боковую поверхность пирамиды.
Задание№8.
На ребре МВ правильной пирамиды МАВС взяты точка К – середина этого ребра и точка L – середина отрезка ВК. Постройте сечение пирамиды плоскостью, проходящей через точку L параллельно прямым КА и МС. Найдите площадь полученного сечения, если сторона основания равна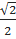 
, а боковое ребро равно 4.
Задание №9.
В основании прямой призмы ABCDA1B1C1D1 лежит ромб ABCD со сторонойи углом А, равным 45°. На ребрах AB, B1C1 и DC взяты соответственно точки E, F и K так, что AE=EB, B1F=FC1 и DK=3KC. Найдите косинус угла между плоскостями EFK и ABC, если высота призмы равна 3.
Задание№10.
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, а боковые ребра равны 7. На ребре AA1 отмечена точка E так, что AE:EA1=2:1. Найдите угол между плоскостями ABC и BED1.
Вариант№11.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(1;-5;2), А2(2;-4;-2), А3(6;-3;-3), А4(2;0;3). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В параллелограмме ABCD даны векторы 
Найти площадь параллелограмма, построенного на диагоналях параллелограмма ABCD.
Задание№3.
Даны три вершины параллелограмма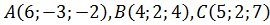 
. Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание№4.
Проверить, лежат ли в одной плоскости точки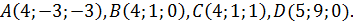 
Найти линейную зависимость вектора 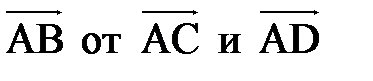, если это возможно.
Задание№5.
Докажите, что через данную точку можно провести плоскость, параллельную двум данным скрещивающимся прямым, и притом только одну.
Задание №6.
Ребро куба АBCDA1B1C1D1 равно 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 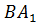грани 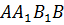и плоскостью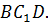
Задание№7.
Найдите угол между скрещивающимися медианами двух граней правильного тетраэдра.
Задание№8.
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=BC= 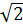, AA1=2 
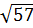. Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол 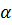=arctg 
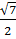. Найдите площадь сечения.
Задание№9.
Диаметр АС основания конуса равен образующей РА этого конуса. Хорда основания ВС составляет угол 300. Найдите косинус угла между прямыми АР и ВС.
Задание№10.
В правильной четырехугольной призме ABСDA1B1C1D1 стороны основания равны 3, а боковые ребра равны 6. На ребре АА1 отмечена точка Е так, что АЕ:ЕА1 = 4:3. Найдите угол между плоскостями АВС и ВЕD1.
Вариант№12.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(-3;12;4), А2(4;-4-30), А3(7;-2;7), А4(-2;13;4). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB= 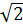, ребро AD= 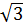, ребро АА1=6. Точка К- середина ребра СС1. Найдите площадь сечения, проходящего через точки A1,D1 и К.
Задание№3.
Точки A(-3;5;-3), B(0;1;10), C(0;6;3), E(5;3;t) служат вершинами параллелепипеда, объем которого равен 36. Найти t.
Задание№4.
Проверить, лежат ли в одной плоскости точки А(-7;3;5), B(2;0;-1), C(6;1;-1), D(-2;5;10). Найти линейную зависимость вектора 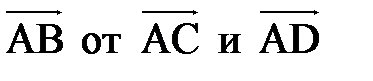, если это возможно.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах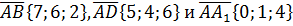 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно 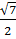. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 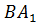грани 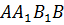и плоскостью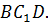
Задание№7.
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что СЕ:ЕС1=2:4. Найдите угол между прямыми ВЕ и АС1.
Задание№8.
В правильной треугольной пирамиде SАВС с вершиной S высота равна 5, а боковые ребра равны 12. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон АВ и АС параллельно прямой SА.
Задание№9.
В правильной четырехугольной пирамиде АВСMT со стороной основания АВ=2 и высотой ТО1=1. Найдите косинус угла между прямыми ОТ и MK, где О и К - середины ребер АВ и ТС.
Задание№10.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны 3, точка D середина ребра A1B1. Найдите тангенс угла между прямыми AD и BC1.
Вариант№13.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(0;6;8), А2(6;3;2), А3(9;4;6), А4(2;8;10). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB=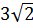 
, ребро AD= 
, ребро АА1=2. Точка К- середина ребра ВВ1. Найдите площадь сечения, проходящего через точки A1,D1 и К.
Задание№3.
Точки A(8;4;6), B(3;0;2), C(1;2;4), E(1;t;2) служат вершинами параллелепипеда, объем которого равен 16. Найти t.
Задание№4.
Проверить, лежат ли в одной плоскости точки А(3;2;3), B(3;-1;1), C(5;0;2), D(-4;3;5) Найти линейную зависимость вектора 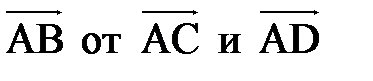, если это возможно.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах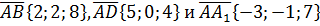 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно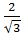 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 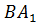грани 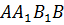и плоскостью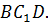
Задание№7.
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка K так, что СЕ:ЕС1=3:2. Найдите угол между прямыми ВK и АС1.
Задание№8.
В правильной треугольной пирамиде МАВС с вершиной М высота равна 6, а боковые ребра равны 9. Найдите площадь сечения этой пирамиды плоскостью, проходящей через середины сторон АВ и АС параллельно прямой МА.
Задание№9.
В правильной четырехугольной пирамиде АВСMT со стороной основания АВ=6 и высотой ТО1=2. Найдите косинус угла между прямыми ОТ и MK, где О и К - середины ребер АВ и ТС.
Задание№10.
В правильной треугольной призме ABCA1B1C1, все ребра которой равны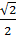 
, точка D середина ребра A1B1. Найдите тангенс угла между прямыми AD и BC1.
Вариант №14.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(2;-3;5), А2(0;-1;-2), А3(3;-4;-3), А4(0;-2;3). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 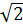, а боковые рёбра равны 8.Найдите площадь сечения пирамиды плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.
Задание№3.
Проверить, лежат ли точки A(2;5;0), B(3;2;4), C(3;0;0), D(2;2;-2) в одной плоскости.
Задание№4.
Точки A(-3;2;-3), B(5;5;5), C(0;1;1), E(5;t;2) служат вершинами параллелепипеда, объем которого равен 36. Найти t.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 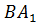грани 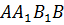и плоскостью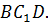
Задание№7.
В прямоугольном параллелепипеде ABCDA1B1C1D1,AB = 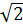, AD=AA1= 
. Найдите угол между прямой АВ1 и плоскостью АВС1.
Задание №8.
Точка Е - середина ребра АА1 куба ABCDA1B1C1D1. Найдите площадь сечения куба плоскостью C1DE, если ребра куба равны .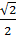
Задание№9.
В правильной четырехугольной пирамиде ABCDS с вершиной S боковое ребро АS вдвое меньше стороны основания АВ. Найдите угол между прямыми AS и BK, где К – точка пересечения медиан грани СDS.
Задание №10.
Длины всех ребер правильной четырехугольной пирамиды SABCD равны 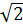. Найдите угол между прямыми SН и ВМ, если отрезок SН - высота пирамиды, точка М - середина ее бокового ребра АS.
Вариант№15.
Задание №1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(-6;-4;-2), А2(1;-3;-5), А3(4;-2;-1), А4(0;2;2). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB= , ребро AD= 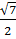, ребро АА1= 
. Точка К- середина ребра ВВ1. Найдите площадь сечения, проходящего через точки A1,D1 и К.
Задание№3.
Даны три вершины параллелограмма А(-4;-1;0), B(1;-3;-5), C(5;-2;-1). Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание№4.
Точки А(-0;-3;-1), В(5;-3;-1), С(5;-3;-5), D(-6;t;2). служат вершинами параллелепипеда, объем которого равен 36. Найти t.
Задание№5.
Докажите, что если точки пересечения медиан треугольников ABC и А1В1С1 совпадают, то прямые АА1, ВВ1 и СС1 параллельны некоторой плоскости.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно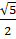 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 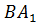грани 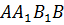и плоскостью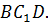
Задание№7.
На ребре СС1 куба ABCDA1B1C1D1 отмечена точка Е так, что СЕ:ЕС1=4:6. Найдите угол между прямыми ВЕ и АС1.
Задание№8.
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=BC= 
, AA1=3 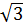. Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол 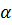=arctg 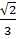. Найдите площадь сечения.
Задание№9.
Найдите площадь сечения правильной четырехугольной пирамиды SАВСD плоскостью, параллельной апофеме SL боковой грани SВС и медиане АМ боковой грани SАВ и проходящей через середину бокового ребра SC, если сторона основания пирамиды равна 4, а расстояние от вершины пирамиды до секущей плоскости равно 30/11.
Задание№10.
В кубе ABCDA1B1C1D1 точки E и K середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Вариант№16.
Задание №1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(-2;0;-3), А2(8;-3;-5), А3(4;-3;-4), А4(-10;0;2). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание №2.
Диагональ основания правильной четырехугольной призмы равна 
, а диагональ призмы наклонена к плоскости основания под углом 45°. Найдите площадь сечения призы, проходящего через сторону нижнего основания и противоположную сторону верхнего основания.
Задание№3.
Даны координаты вершин параллелепипеда: A(-0;-5;-3), B(5;-6;-10), C(7;-5;-3), D(-6;2;2). Найти объем параллелепипеда, его высоту, опущенную из вершины С, угол между вектором AD и гранью, в которой лежат векторы АВ и АС.
Задание №4.
Проверить, лежат ли в одной плоскости точки A(6;4;1), B(5;2;7), C(3;7;0), D(0;2;1). Найти линейную зависимость вектора 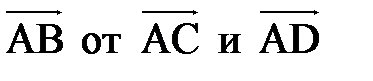, если это возможно.
Задание №5.
Докажите, что если точки пересечения медиан треугольников ABC и А1В1С1 совпадают, то прямые АА1, ВВ1 и СС1 параллельны некоторой плоскости.
Задание №6.
Ребро куба АBCDA1B1C1D1 равно 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 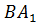грани 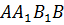и плоскостью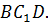
Задание №7.
Найдите расстояние между скрещивающимися диагоналями АВ1 и ВС1 смежных граней АА1В1В и ВВ1С1С куба ABCDA1B1C1D1, если ребро этого куба равно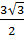 
.
Задание №8.
В кубе ABCDA1B1C1D1 со стороной a точка K является серединой стороны верхнего основания B1C1, точка L делит другую сторону C1D1 этого основания в отношении 4:3, считая от вершины С1, точка N является серединой бокового ребра АА1. Найдите площадь сечения, проходящего через точки К, L, N.
Задание№9.
В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 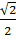, найдите косинус угла между прямыми AB и CA 1.
Задание №10.
В правильной прямоугольной призме ABCA 1 B 1 C 1все ребра которой равны 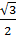найдите квадрат косинуса угла между прямыми АВ и А1С.
Вариант№17.
Задание№1.
Даны координаты вершин пирамиды А1А2А3А4:
А1(5;0;5), А2(7;6;3), А3(1;2;3), А4(7;0;1). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В основании треугольной пирамиды SABC лежит прямоугольный треугольник АВС. Середина D гипотенузы этого треугольника является основанием высоты SD данной пирамиды. Известно, что SD=2, AC=4, BC=9. Через середину высоты SD проведено сечение пирамиды плоскостью, параллельной ребрам AC и SB. Найти площадь этого сечения.
Задание№3.
Даны три вершины параллелограммаA(5;7;2), B(8;3;0), C(6;0;3). Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание №4.
Проверить, лежат ли в одной плоскости точки А(5;1;1), В(1;0;2), С(7;5;-1), D(1;-4; 1). Найти линейную зависимость вектора 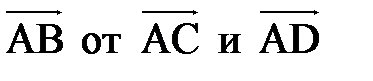, если это возможно.
Задание№5.
Дан параллелепипед ABCDA1B1C1D1 построенный на векторах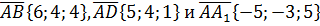 
. Найти высоту, проведенную из вершины A1 на грань ABCD.
Задание№6.
Ребро куба АBCDA1B1C1D1 равно . Найдите:
а) расстояние от вершины С до плоскости BDC1;
б) угол между диагональю 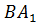грани 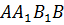и плоскостью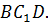
Задание№7.
Основание пирамиды – прямоугольник со сторонами 6 и 10. Одно из боковых рёбер перпендикулярно плоскости основания и равно 3. Найдите расстояние между этим ребром и скрещивающейся с ним диагональю основания, а также боковую поверхность пирамиды.
Задание№8.
На ребре МВ правильной пирамиды МАВС взяты точка К – середина этого ребра и точка L – середина отрезка ВК. Постройте сечение пирамиды плоскостью, проходящей через точку L параллельно прямым КА и МС. Найдите площадь полученного сечения, если сторона основания равна 
, а боковое ребро равно 2.
Задание №9.
В основании прямой призмы ABCDA1B2C3D4 лежит ромб ABCD со сторонойи углом А, равным 35°. На ребрах AB, B1C1 и DC взяты соответственно точки E, F и K так, что AE=EB, B1F=FC1 и DK=3KC. Найдите косинус угла между плоскостями EFK и ABC, если высота призмы равна 8.
Задание№10.
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 2, а боковые ребра равны 5. На ребре AA1 отмечена точка E так, что AE:EA1=3:1. Найдите угол между плоскостями ABC и BED1.
Вариант№18.
Даны координаты вершин пирамиды А1А2А3А4:
А1(6;-8;4), А2(5;-2;-8), А3(6;-9;-63), А4(3;1;5). Найти:
1)Длину ребра А1А2;
2) Угол между ребрами А1А2 и А1А4;
3) Угол между ребром А1А4 и гранью А1А2А3;
4) Площадь грани А1А2А3;
5) Объем пирамиды.
Задание№2.
В параллелограмме ABCD даны векторы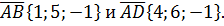 
Найти площадь параллелограмма, построенного на диагоналях параллелограмма ABCD.
Задание№3.
Даны три вершины параллелограмма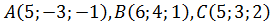 
. Найти длину высоты, опущенной из вершины С (через площадь параллелограмма).
Задание№4.
Проверить, лежат ли в одной плоскости точки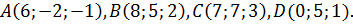 
Найти линейную зависимость вектора 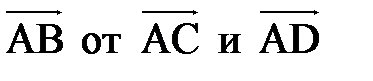, если это возможно.
Задание№5.
Докажите, что через данную точку можно провести плоскость, параллельную двум данным скрещивающимся прямым, и притом только одну.
Задание №6.
Ребро куба АBCDA1B1C1D1 равно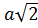 
. Найдите:
а) расстояние от вершины С до плоскости BDC1;
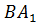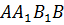б) угол между диагональю грани и плоскостью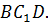
Задание№7.
Найдите угол между скрещивающимися медианами двух граней правильного тетраэдра.
Задание№8.
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=BC= 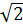, AA1=2 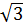. Сечение параллелепипеда проходит через точки B и D и образует с плоскостью ABC угол 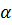=arctg . Найдите площадь сечения.
Задание№9.
Диаметр АС основания конуса равен образующей РА этого конуса. Хорда основания ВС составляет угол 450. Найдите косинус угла между прямыми АР и ВС.
Задание№10.
В правильной четырехугольной призме ABСDA1B1C1D1 стороны основания равны 8, а боковые ребра равны 12. На ребре АА1 отмечена точка Е так, что АЕ:ЕА1 = 6:3. Найдите угол между плоскостями АВС и ВЕD1.
Вариант№19.
<
