Краткие теоретические сведения
Все математические задачи, решаемые в теории автоматического управления, можно объединить в два больших класса:
· задачи анализа;
· задачи синтеза.
В задачах анализа полностью известна структура системы, заданы все (как правило) параметры системы, и требуется оценить какое-либо ее статическое или динамическое свойство. К задачам анализа относятся определение устойчивости (см. главу 5) и оценка качества управления (см. главу 6) системы.
Задачи синтеза можно рассматривать как обратные задачам анализа: в них требуется определить структуру и параметры системы по заданным показателям качества управления. Простейшими задачами синтеза являются, например, задачи определения передаточного коэффициента разомкнутой АСУ по заданной ошибке или условию минимума интегральной оценки.
Синтез АСУ – процедура определения структуры и параметров системы по заданным показателям качества управления.
В общем случае при проектировании системы необходимо определить алгоритмическую и функциональную структуры системы, т. е. решить задачу полного синтеза.
Определение алгоритмической структуры (теоретический синтез) производится с помощью математических методов и на основании требований, записанных в четкой математической форме.
Определение функциональной структуры (технический синтез) заключается в выборе конкретных физических элементов и согласования их между собой по статическим и энергетическим характеристикам. Эта процедура не имеет пока строгой математической основы (т. е. не формализована) и поэтому относится к области инженерного творчества.
С учетом того, что не любой элемент алгоритмической структуры может иметь отображение в виде физического блока функциональной структуры, т. е. просто не может быть реализован, задачу синтеза в большинстве случаев невозможно решать, определяя сначала алгоритмическую структуру АСУ, а затем по ней – функциональную структуру. Процедуры определения алгоритмической и функциональной структур тесно переплетаются друг с другом. Окончательное решение о структуре АСУ принимается на основе компромисса между качеством управления, с одной стороны, и простотой и надежностью, с другой.
Заключительным этапом проектирования АСУ является параметрическая оптимизация – определение настроечных параметров выбранного регулятора.
После решения задачи синтеза обычно выполняют анализ синтезированной системы, т. е. проверяют, обладает ли система необходимыми показателями устойчивости и качества управления.
Ход выполнения работы
Выбор объекта регулирования
При решении задач автоматизации технологических процессов часто приходится иметь дело с инерционными статическими объектами управления (например, с электрическими двигателями), переходные характеристики h0(t), которых имеют специфическую s-образную форму (рис. 1). Наклон, кривизна характеристики и ее расстояние от оси ординат зависят от динамических свойств конкретного объекта

Рис. 1. Переходные характеристики реального объекта (1)
и его приближенной модели второго порядка (2) с запаздыванием
Для практических расчетов АСУ такими объектами каждую s - образную кривую, снятую при единичном ступенчатом воздействии, достаточно охарактеризовать следующими параметрами, определяемыми непосредственно по графику:
· передаточным коэффициентом k0;
· постоянной времени T0;
· полные запаздывание t0.
Параметры T0 и t0 определяют проведением касательной АВ к наиболее крутому участку переходной характеристики h0(t).
При расчете настроечных параметров АСУ с объектами, имеющими s - образные переходные характеристики, ориентируются либо непосредственно на параметры k0, T0, t0, которыеобобщенно характеризуют статику и динамику реального объекта, либо используют упрощенные модели объекта, коэффициенты которых однозначно выражаются через указанные экспериментальные параметры.
Рассчитаем настроечные параметры АСУ при помощи упрощенной модели объекта
На практике наиболее часто приходится решать задачу синтеза АСУ с инерционными объектами управления с запаздыванием, которые можно описать следующей обобщенной передаточной функцией
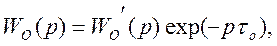
где  - дробно-рациональная функция, характеризующая инерционную часть объекта управления;
- дробно-рациональная функция, характеризующая инерционную часть объекта управления;
tо – чистое запаздывание объекта управления.
Упрощенные модели объектов:
Наиболее простой, но и менее точной является модель первого порядка
 , (1)
, (1)
где  ;
;  .
.
Модель первого порядка состоит из апериодического звена и звена Transport Delay, соединённых последовательно.
Достаточно хорошее приближение к s - образным переходным характеристикам дает модель второго порядка с запаздыванием и одинаковыми постоянными времени (рис. 1)
 , (2)
, (2)
где  ;
;  .
.
Модель второго порядка состоит из апериодического звена, звена с чистым запаздыванием и звена Transport Delay, соединённых последовательно.
Существуют и более сложные модели, например, модель второго порядка с запаздыванием и разными постоянными времени
 (3)
(3)
2. Выбор регулятора.
Регулятор устанавливает связь ошибки e(p) и управляющего воздействия Y(p),
Эта связь в типовой одноконтурной АСУ (рис. 2) определяется передаточной функцией регулятора
 (4)
(4)

рис. 2
В простейшем случае, когда возмущающее воздействие на объект отсутствует (X(p) =0), управление можно осуществлять по разомкнутой схеме (рис. 3) при передаточной функции регулятора

так как передаточная функция АСУ

Это означает мгновенное воспроизведение выходной величиной задающего воздействия

Такой переходный процесс называют идеальным, а алгоритмическую структуру его обеспечивающую – идеальной.

Рис.3. Алгоритмическая схема идеальной АСУ
В линейных АСУ применяются следующие типовые алгоритмы управления (регулирования):
- пропорциональный (П) алгоритм;
- интегральный (И) алгоритм;
- пропорционально-интегральный (ПИ) алгоритм;
- пропорционально-дифференциально-интегральный (ПИД) алгоритм;




