Если функция 
имеет непрерывные частные производные второго порядка, то дифференциал второго порядка определяется так: 
.
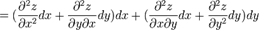
Символически общий вид дифференциала n-го порядка от функции 
выглядит следующим образом:
где 
, а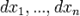 
произвольные приращения независимых переменных 
.
Приращения 
рассматриваются как постоянные и остаются одними и теми же при переходе от одного дифференциала к следующему. Сложность выражения дифференциала возрастает с увеличением числа переменных.
20.Свойства функций, дифференцируемых на интервале: Теорема Ролля. Теорема Коши. Теорема Лагранжа.
Теорема Ролля. Если ф-ция y=f(x) непрерывна на [a,b] и дифференцируема на (a,b) и значения ф-ции на концах отрезка одинаковы, т.е. f(a)=f(b), то существует на (a,b) т.ξ, в которой производная ф-ции=0. Для док-ва воспользуемся одной из теорем о непрерывных ф-циях, а именно: непрерывная на [a,b] ф-ция принимает на этом отрезке свое max и min значение: 1) Если fmax=fmin, то f(x)=const. 2) Если fmax>fmin, то по крайней мере одно из этих значений ф-ция принимает в т.ξϵ(a,b). Пусть например f(ξ)= fmax, тогда приращению аргумента ∆х>0 будет соответствовать приращение ф-ции f(x+∆x)-f(x)<=0, f(x-∆x)-f(x)<=0, откуда, разделив на ∆x оба соотношения получим, сохранив знак: (f(x+∆x)-f(x))/ ∆x<=0, (f(x-∆x)-f(x))/ -∆x>=0. Выполнив предельные переходы этих нер-в получим при x=ξ: f ′(ξ)<=0, f ′(ξ)>=0, => f ′(ξ)=0.
Теорема Коши. Если ф-ции f(x) и φ(x) непрерывны на [a,b], дифференцируемы на (a,b) и производная φ′(x)=0 во всех точках (a,b), то существует хотя бы одна точка ξ такая, что (f(b)-f(a))/ (φ(b)-φ(a))=f ′(ξ)/φ′(ξ) (1).
Док-во: введем вспомог ф-цию F(x)=f(x)+λφ(x), причем λ выбирается из условия, чтобы f(a)=f(b), т.е. мы подгоняем F(x) под условие Т.Ролля. Для этого нужно найти λ, соотв. этим условиям: f(а)+λφ(а)= f(b)+λφ(b). λ= (f(b)- f(а))/(φ(b)-φ(а)). Подставим ее во вспомог ф-цию:
F(x)=f(x)+ (f(b)- f(а))/(φ(b)-φ(а))φ(x)=0. При φ(ξ)≠0 нетрудно найти (f(b)- f(а))/(φ(b)-φ(а))= f ′(ξ)/φ′(ξ).
Теорема Лагранджа. Если ф-ция f(x) непрерывна на [a,b] и дифференцируема на (a,b), то существует хотя бы одна т.ξϵ(a,b) такая, что f(b)-f(a)=f ′(ξ)(b-a) (2).
Док-во: ф-ла (2) есть частный случай (1). Положим в (1) φ(x)=x, при этом φ′(x)=x′=1, φ(a)=a, φ(b)=b. В ф-ле Коши получим: (f(b)-f(a))/(b-a)= f ′(ξ), откуда следует (2).
Приложение формулы Тейлора к исследованию функции:
Возрастание и убывание ф-ии.достаточное условие возрастания.
Функция y=f(x), определенная на некотором отрезке [ a, b ] (интервале (a, b)), называется возрастающей на этом отрезке, если большему значению аргумента x из [ a, b ] соответствует большее значение функции, то есть если x 1 < x 2, то f(x 1 ) < f(x 2 ).
Функция y=f(x) называется убывающей на некотором отрезке [ a, b ], если меньшему значению аргумента x из [ a, b ]соответствует большее значение функции, то есть если x 1 < x 2, то f(x 1 ) > f(x 2 ).
Функция, только возрастающая или только убывающая на отрезке, называется монотонной на этом отрезке.
Функция y=f(x) называется постоянной на некотором отрезке [ a, b ], если при изменении аргумента x она принимает одни и те же значения.
Т1*. (Необходимое и достаточное условия возрастания функции)
Если дифференцируемая функция y=f(x) возрастает на [ a, b ], то ее производная неотрицательна на этом отрезке, f '(x) ≥ 0.
Обратно. Если функция y=f(x) непрерывна на [ a, b ], дифференцируема на (a, b) и ее производная положительна на этом отрезке, f ' (x) ≥ 0 для a<x<b, то f(x) возрастает на[ a, b ].
*Точка х0 называется точкой максимума функции у=ƒ(х), если существует такая d -окрестность точки х0, что для всех х≠х0 из этой окрестности выполняется неравенство ƒ(х)<ƒ(х0).
Аналогично определяется точка минимума функции: x0 — точка минимума функции, если $d>0 " х: 0<|x-x0|<d Þ ƒ(х)>ƒ(х0). Значение функции в точке максимума (минимума) называется максимумом (минимумом) функции. Максимум (минимум) функции называется экстремумом функции.
непрерывная функция может иметь экстремум лишь в точках, где производная функции равна нулю или не существует. Такие точки называются критическими.
*(достаточное условие экстремума). Если непрерывная функция у=ƒ(х) дифференцируема в некоторой d -окрестности критической точки х0 и при переходе через нее (слева направо) производная ƒ'(х) меняет знак с плюса на минус, то х0 есть точка максимума; с минуса на плюс, то х0 — точка минимума.
*правило исследования функции на экстремум:
1) найти критические точки функции у=ƒ(х);
2) выбрать из них лишь те, которые являются внутренними точками области определения функции;
3) исследовать знак производной ƒ'(х) слева и справа от каждой из выбранных критических точек;
4) в соответствии с теоремой (достаточное условие экстремума) выписать точки экстремума (если они есть) и вычислить значения функции в них.
*выпуклость и вогнутость.
График дифференцируемой функции у=ƒ(х) называется выпуклым вниз на интервале (а;b), если он расположен выше любой ее касательной на этом интервале. График функции у=ƒ(х) называется выпуклым вверх на интервале (а;b), если он расположен ниже любой ее касательной на этом интервале.
Если функция у=ƒ(х) во всех точках интервала (а;b) имеет отрицательную вторую производную, т. е. ƒ"(х)<0, то график функции в этом интервале выпуклый вверх. Если же ƒ"(х)>0 " xє(а;b) — график выпуклый вниз.
точка графика непрерывной функции у=ƒ(х), отделяющая его части разной выпуклости, называется точкой перегиба.
(достаточное условие существования точек перегиба). Если вторая производная ƒ"(х) при переходе через точку х0, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой х0 есть точка перегиба.
Пусть ƒ"(х)<0 при х<х0 и ƒ"(х)>0 при х>х0. Это значит, что слева от х=х0 график выпуклый вверх, а справа — выпуклый вниз. Следовательно, точка (х0;ƒ(х0)) графика функции является точкой перегиба.
Аналогично доказывается, что если ƒ"(х)>0 при х<x0 и ƒ"(х)<0 при х>х0, то точка (х0;ƒ(х0)) — точка перегиба графика функции у=ƒ(х).
асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой.
Асимптоты могут быть вертикальными, на клонными и горизонтальными.
Говорят, что прямая х=а является вертикальной асимптотой графика функции
, или 
Для отыскания вертикальных асимптот нужно найти те значения х, вблизи которых функция ƒ (х) неограниченно возрастает по модулю. Обычно это точки разрыва второго рода.
47(22) ФОРМУЛА ТЕЙЛОРА
Напомним, что в случае функции одного переменного 
формула Тейлора имеет вид
| |
|
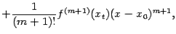
где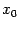 
-- фиксированная точка, в которой ведётся разложение, -- текущая точка, а 
-- некоторая точка отрезка между точкам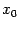и и . При этом предполагается, что функция 
имеет производную 
-го порядка, определённую в некоторой окрестности точки .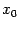
Последнее слагаемое формулы, то есть 
называется остаточным членом формулы Тейлора, а многочлен от , равный
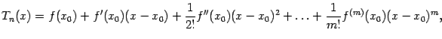
называется многочленом Тейлора функции в точке .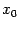
49(24)
Выпуклость и вогнутость графика функции
График функции y = f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.
График функции y = f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.
На рисунке показана кривая, выпуклая на (a; b) и вогнутая на (b; c).
Рассмотрим достаточный признак, позволяющий установить, будет ли график функции в данном интервале выпуклым или вогнутым.
Теорема. Пусть y = f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f ''(x) > 0 – вогнутый.
Доказательство. Предположим для определенности, что f ''(x) < 0 и докажем, что график функции будет выпуклым.
Возьмем на графике функции y = f(x) произвольную точку M0 с абсциссой x0 Î (a; b) и проведем через точку M0 касательную. Ее уравнение  . Мы должны показать, что график функции на (a; b) лежит ниже этой касательной, т.е. при одном и том же значении x ордината кривой y = f(x) будет меньше ордината касательной.
|  
|
Итак, уравнение кривой имеет вид y = f(x). Обозначим 
ординату касательной, соответствующую абсциссе x. Тогда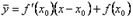 
. Следовательно, разность ординат кривой и касательной при одном и том же значении x будет 
.
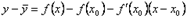Разность f(x) – f(x0) преобразуем по теореме Лагранжа 
, где c между x и x0.
Таким образом, 
.
К выражению, стоящему в квадратных скобках снова применим теорему Лагранжа: 
, где c1 между c0 и x0. По условию теоремы f ''(x) < 0. Определим знак произведения второго и третьего сомножителей.
1. Предположим, что x > x 0. Тогда x0 < c1 < c < x, следовательно, 
(x – x 0) > 0 и (c – x 0) > 0. Поэтому 
.
2. Пусть x < x0, следовательно, x < c < c 1 < x 0 и (x – x 0) < 0, (c – x 0) < 0. Поэтому вновь .
Таким образом, любая точка кривой лежит ниже касательной к кривой при всех значениях x и x0 Î (a; b), а это значит, что кривая выпукла. Вторая часть теоремы доказывается аналогично.
Достаточное условие вогнутости (выпуклости) функции.
Пусть функция f (x) дважды дифференцируема (имеет вторую производную) на интервале (a, b), тогда:
если f '' (x) > 0 для любого x 
(a, b), то функция f (x) является вогнутой на интервале (a, b);
если f '' (x) < 0 для любого x (a, b), то функция f (x) является выпуклой на интервале (a, b).
23. Разложение по формуле Маклорена некоторых элементарных функций.
Ряд Маклорена:
Экспонента:
Натуральный логарифм:
для всех
§ Синус:
§ Косинус:
§ Тангенс: для всех 
 |
§ 
Арксинус: для всех
 |
§ Арктангенс: для всех
 |
