Первый и второй замечательные пределы. Их следствия.
Док-во:имеем окр радиуса=R.построим соотвествующие фигуры 
 где
где  — площадь сектора
— площадь сектора  )
)
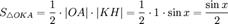


 (из
(из  :
:  )
)

предположим,что x>0,тогда sinx>0,тогда знак деления не изменится при делении на sinx,

Перейдём к пределу:



Следствия



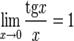
 На основании связи ББ и БМ величин имеет место следующее нер-во:
На основании связи ББ и БМ величин имеет место следующее нер-во:  второй замечательный предел
второй замечательный предел
Следствия
1. 
2. 
3. 
4. 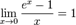
 для
для  ,
, 
35(10)Таблица эквивалентных бесконечно малых

11. Непрерывность отображения. Непрерывность числовой функции одной переменной, нескольких переменных.
Ф-ция f(x) наз. непрерывной в точке x0 слева, если существует предел этой ф-ции слева и он = значению f(x0). При x→x0-0 lim f(x)=f(x0-0)=f(x0). Аналогично и для непрерывности справа. Если ф-ция непрерывна как слева, так и справа в т. x0, то она непрерывна в самой т. x0. Отсюда вытекает: f(x0-0)= f(x0+0)=f(x0). Таким образом, ф-ция непрерывна в т.x0, если при x→x0 lim f(x)= f(x0). БМ приращению аргумента x будет соответствовать БМ приращение ф-ции y=f(x): при ∆x→0 lim ∆y=0. Аналогично и для ф-ции нескольких переменных.
 По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой точке равен ее значению в ней:
По определению функция f (x, y) непрерывна в точке (х0, у0), если она определена в некоторой ее окрестности, в том числе в самой точке (х0, у0) и если предел f (x, y) в этой точке равен ее значению в ней:
Можно ввести приращение Δu функции и = f (x, y) в точке (x, y), соответствующее приращениям Δх, Δу аргументов Δu = f (х + Δх, у + Δу) – f (x, y) и на этом языке определить непрерывность f(x, y): функция f непрерывна в точке (x, y), если
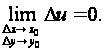
Если условия непрерывности нарушены, то ф-ция терпит разрыв.
37(12)Точки разрыва,классификация точек разрыва.
Функция f(x) называется непрерывной в точке  , если предел слева равен пределу справа и совпадает со значением функции в точке
, если предел слева равен пределу справа и совпадает со значением функции в точке  , то есть
, то есть  .Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.
.Следует отметить также, что непрерывность функции может быть односторонней. Поясним это следующим образом.  Если односторонний предел
Если односторонний предел  , то функция называется непрерывной справа. Если односторонний предел
, то функция называется непрерывной справа. Если односторонний предел 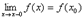 , то функция называется непрерывной слева. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы. в точке разрыва 1 – го рода функция может иметь только конечный скачок. иногда точку разрыва 1–го рода еще называют устранимой точкой разрыва Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
, то функция называется непрерывной слева. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке.Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы. в точке разрыва 1 – го рода функция может иметь только конечный скачок. иногда точку разрыва 1–го рода еще называют устранимой точкой разрыва Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
Частные производные и полный дифференциал функции нескольких переменных.
частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной). частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов: 
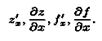 Аналогично определяется и обозначается частная производная от z=ƒ(х;у) по переменной у:
Аналогично определяется и обозначается частная производная от z=ƒ(х;у) по переменной у:
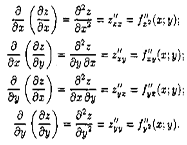
 Частные производные
Частные производные 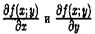 называют частными производными первого порядка. Их можно рассматривать как функции от (х;у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
называют частными производными первого порядка. Их можно рассматривать как функции от (х;у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
Аналогично определяются частные производные 3-го, 4-го и т. д. порядков.
Так, 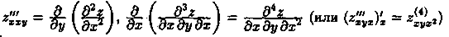 и т.д. Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной
и т.д. Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной
формулу для вычисления полного дифференциала. 
или  где
где 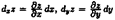 — частные дифференциалы функции z=ƒ(х;у).
— частные дифференциалы функции z=ƒ(х;у).
Теоре.(достаточное условие дифференцируемости функции). Если функция z = ƒ(х;у) имеет непрерывные частные производные z'x и z'y в точке М(х;у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой (44.5).Отметим, что для функции у=ƒ(х) одной переменной существование производной ƒ'(х) в точке является необходимым и достаточным условием ее дифференцируемости в этой точке.Чтобы функция z=ƒ(х;у) была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.
38(13)
| |
Свойство 1: (Первая теорема Вейерштрасса (Вейерштрасс Карл (1815-1897) - немецкий математик)). Функция, непрерывная на отрезке, ограничена на этом отрезке, т.е. на отрезке  выполняется условие - выполняется условие -  .Доказательство этого свойства основано на том, что функция, непрерывная в точке .Доказательство этого свойства основано на том, что функция, непрерывная в точке  , ограничена в некоторой ее окрестности, а если разбивать отрезок , ограничена в некоторой ее окрестности, а если разбивать отрезок  на бесконечное количество отрезков, которые “стягиваются” к точке на бесконечное количество отрезков, которые “стягиваются” к точке  , то образуется некоторая окрестность точки , то образуется некоторая окрестность точки  .
Свойство 2: Функция, непрерывная на отрезке .
Свойство 2: Функция, непрерывная на отрезке  , принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения , принимает на нем наибольшее и наименьшее значения.
Т.е. существуют такие значения  и и  , что , что  , причем , причем  .
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например - .
Отметим эти наибольшие и наименьшие значения функция может принимать на отрезке и несколько раз (например -  ).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке ).
Разность между наибольшим и наименьшим значением функции на отрезке называется колебанием функции на отрезке.
Свойство 3: (Вторая теорема Больцано - Коши). Функция, непрерывная на отрезке  , принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция , принимает на этом отрезке все значения между двумя произвольными величинами.
Свойство 4: Если функция  непрерывна в точке непрерывна в точке  , то существует некоторая окрестность точки , то существует некоторая окрестность точки  , в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция , в которой функция сохраняет знак.
Свойство 5: (Первая теорема Больцано (1781-1848) - Коши). Если функция  - непрерывная на отрезке - непрерывная на отрезке  и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого
отрезка, где и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого
отрезка, где  .
Т.е. если .
Т.е. если  , то , то  .
Определение. Функция .
Определение. Функция  называется равномерно непрерывной на отрезке называется равномерно непрерывной на отрезке  , если для любого , если для любого  существует существует  такое, что для любых точек такое, что для любых точек  и и  таких, что таких, что  верно неравенство верно неравенство  .
Отличие равномерной непрерывности от “обычной” в том, что для любого существует свое .
Отличие равномерной непрерывности от “обычной” в том, что для любого существует свое  , не зависящее от , не зависящее от  , а при “обычной” непрерывности , а при “обычной” непрерывности  зависит от зависит от  и и  .
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) - немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Свойство 7: Если функция .
Свойство 6: Теорема Кантора (Кантор Георг (1845-1918) - немецкий математик). Функция, непрерывная на отрезке, равномерно непрерывна на нем. (Это свойство справедливо только для отрезков, а не для интервалов и полуинтервалов.)
Свойство 7: Если функция  определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция  тоже однозначна, монотонна и непрерывна. тоже однозначна, монотонна и непрерывна.
|
Свойства функций, непрерывных в точке
Поскольку точки 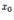 непрерывности функции
непрерывности функции  задаются условием
задаются условием  , то часть свойств функций, непрерывных в точке
, то часть свойств функций, непрерывных в точке  , следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.
, следует непосредственно из свойств пределов. Сформулируем их в виде следующей теоремы.
Теорема 1 Пусть функции  и
и  непрерывны в точке
непрерывны в точке  . Тогда функции
. Тогда функции  ,
,  ,
, 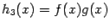 непрерывны в точке
непрерывны в точке  . Если
. Если  , то функция
, то функция  также непрерывна в точке
также непрерывна в точке  .
.
Доказательство. Оно сразу же следует из теорем о пределах 2.8, 2.9, 2.10 и следствия 2.5.
Как непосредственное следствие этой теоремы получается следующее
Предложение 3.3 Рассмотрим множество всех функций, определённых в некоторой фиксированной окрестности  точки
точки  и непрерывных в этой точке. Тогда это множество
и непрерывных в этой точке. Тогда это множество  является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:
является линейным пространством, то есть замкнуто относительно сложения и умножения на постоянные:
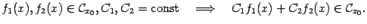
Доказательство. Действительно, постоянные  и
и 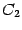 -- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке
-- это непpеpывные функции (в любой точке); по пpедыдущей теоpеме тогда непpеpывны в точке  пpоизведения
пpоизведения  и
и  . Но тогда по этой же теоpеме непpеpывна в точке
. Но тогда по этой же теоpеме непpеpывна в точке  и сумма
и сумма  .
.
Теорема 2 Пусть функции  и
и  таковы, что существует композиция
таковы, что существует композиция  ,
,  . Пусть функция
. Пусть функция  непрерывна в точке
непрерывна в точке 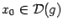 , а функция
, а функция  непрерывна в соответствующей точке
непрерывна в соответствующей точке  . Тогда композиция
. Тогда композиция  непрерывна в точке
непрерывна в точке  .
.
Доказательство. Заметим, что равенство  означает, что при
означает, что при  будет
будет  . Значит,
. Значит,

(последнее равенство следует из непрерывности функции  в точке
в точке 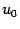 ). Значит,
). Значит,

а это равенство означает, что композиция  непрерывна в точке
непрерывна в точке  .
.
Заметим, что, очевидно, в предыдущих двух теоремах можно было бы заменить базу 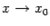 на односторонние базы
на односторонние базы  или
или  и получить аналогичные утверждения для непрерывности слева или справа:
и получить аналогичные утверждения для непрерывности слева или справа:
Теорема 3 Пусть функции  и
и  непрерывны слева (справа) в точке
непрерывны слева (справа) в точке  . Тогда функции
. Тогда функции  ,
, 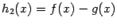 ,
,  непрерывны слева (соотв. справа) в точке
непрерывны слева (соотв. справа) в точке  . Если
. Если  , то функция
, то функция  также непрерывна слева (спpава) в точке
также непрерывна слева (спpава) в точке  .
.
Теорема 4 Пусть функция  непрерывна слева (справа) в точке
непрерывна слева (справа) в точке  , а функция
, а функция  непрерывна в точке
непрерывна в точке 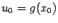 . Тогда композиция
. Тогда композиция  непрерывна слева (соотв. справа) в точке
непрерывна слева (соотв. справа) в точке  .
.
14. Дифференциал отображения. Дифференциал и производная числовой функции одной переменной. Таблица производных. Дифференцируемость.
Пусть есть отображение, кот вычисляется так: ∆y=f(x+∆x)-f(x) (1). В общем случае ∆y зависит не только от ∆х, но и от нач.вектора х. Т.е. ∆y=∆y(x;∆x). Пусть при ∆х<ε приращение отображения (1) можно представить в виде ∆y=dy+0(|∆x|) (2), где dy= dy(x;∆x). 0(|∆x|) – это БМ величина высшего порядка по сравнению с ∆x, т.е. при |∆x|→0 lim 0(|∆x|)/|∆x|=0. Величина dy называется дифференциалом отображения. Отображение, для кот. существует дифференциал, т.е. имеет место (2), называется дифференцируемым. Понятие дифференцируемости можно рассм для отдельных точек Х или его подмножеств. Это общее понятие дифференциала. Его можно конкретизировать: 1) y=f(x): R→R; 2) для числ ф-ции многих переменных y=f(x1,x2…xn): Rn→R; 3) для вектора ф-ции скалярного аргумента y=f(с палочкой)(x): R→ Rn.
Линейное отображение по ∆x будет иметь вид a*∆x, где ∆xϵR, aϵR; При этом a может зависеть от нач.вектора х. Тогда dy=a(x)∆x (5). Отсюда согласно (2) ∆y= a(x)∆x+0(∆x). Разделим на ∆x и перейдем к пределу (все пределы при ∆x→0) lim ∆y/∆x=lim a(x) + lim 0(∆x)/ ∆x; y′=a(x); Таким образом, a(x) – производная ф-ции f(x), тогда (5) принимает вид dy=f ′(x)∆x. При рассм ф-ции y=x y′=x′=1, тогда dx=∆x, => dy=f ′(x)dx – дифференциал числовой ф-ции одной переменной. Отсюда следует, что f ′(x)= dy/ dx, т.е. производная ф-ции y=f(x) равна отношению дифференциала ф-ции к дифференциалу аргумента.
41(16)

Производные Функций Нескольких Переменных.
Рассмотрим функцию u = F (x), определенную в некоторой области D. Пусть  − фиксированная точка. Дадим координате х 1 приращение
− фиксированная точка. Дадим координате х 1 приращение  . Если существует конечный предел
. Если существует конечный предел  , то он называется частной производной функции F (x) по переменной х 1 и обозначается
, то он называется частной производной функции F (x) по переменной х 1 и обозначается 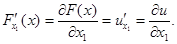
Аналогично определяются частные производные по всем остальным переменным.
Замечания.
1. Частная производная по какой либо переменной есть обычная производная, при условии, что все остальные переменные – константы.
2. Последнее обозначение, в отличие от функций одной переменной, не равно частному от деления двух дифференциалов, а является неразрывным символом.
В частном случае двух переменных частная производная равна тангенсу наклона касательной к сечению поверхности плоскостью, перпендикулярной ко второй переменной.
Полный дифференциал функции нескольких переменных.
Пусть задана функция  . Если аргументу
. Если аргументу  сообщить приращение
сообщить приращение  , а аргументу
, а аргументу 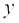 – приращение
– приращение  , то функция
, то функция  получит приращение
получит приращение  , которое называется полным приращением функции и определяется формулой:
, которое называется полным приращением функции и определяется формулой:  Функция
Функция  , полное приращение
, полное приращение 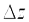 которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно
которой в данной точке может быть представлено в виде суммы двух слагаемых (выражения, линейного относительно 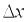 и
и  , и величины бесконечно малой высшего порядка относительно
, и величины бесконечно малой высшего порядка относительно  ):
):
 ,
,
где  и
и  стремятся к нулю, когда
стремятся к нулю, когда 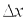 и
и  стремятся к нулю (т.е. когда
стремятся к нулю (т.е. когда  ), называется дифференцируемой в данной точке. Линейная (относительно
), называется дифференцируемой в данной точке. Линейная (относительно 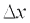 и
и  ) часть полного приращения функции называется полным дифференциалом и обозначается
) часть полного приращения функции называется полным дифференциалом и обозначается  :
:
 ,
,
где  и
и 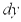 – дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям
– дифференциалы независимых переменных, которые, по определению, равны соответствующим приращениям  и
и 
17.Производные неявной функции одной и нескольких переменных.
Как известно, неявная числовая ф-ция одной переменной y=y(x) опред уравнением F(x,y)=0 (1). В этом равенстве правую и левую части можно рассм как сложные ф-ции от х и продифференцировать: Fx′(x,y)=0x′; (д F/ д x)+(д F/ д y)(d y/ d x)=0; d y/ d x=-(д F/ д x)/(д F/ д y), дF/дy≠0.
Рассм неявную ф-цию двух переменных. z=z(x,y), F(x,y,z)=0. Применяя вышеприведенные способы, будем дифференцировать это выражение по x и по y: (д F/ д x)+ (д F/ д z)(d z/ d x)=0; д F/ д x≠0; d z/ d x=-(д F/ д x)/(д F/ д z). Аналогично, d z/ d y=-(д F/ д y)/(д F/ д z).
18.Производные и дифференциалы высших порядков для числовой функции 1ой переменной.
Для числовой ф-ии 2х переменных Z=f(x,y)частные производные высших порядков вводятся аналогично тому,как это сделано для ф-ии одной переменной ðz/ðx=fₓ’(x,y) ðz/ðy=f’y(x,y)
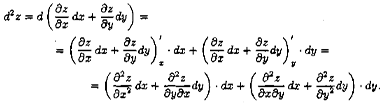 Дифференциал второго порядка определяется по формуле (d2z = d(dz). Найдем его:
Дифференциал второго порядка определяется по формуле (d2z = d(dz). Найдем его:
Отсюда: 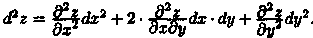 Символически это записывается так:
Символически это записывается так:
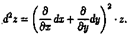
Методом математической индукции можно показать, что 
Отметим, что полученные формулы справедливы лишь в случае, когда переменные х и у функции z = ƒ(х;у) являются независимыми.Если z = ƒ(х;у) — дифференцируемая в точке М(х;у) є D функция и х = x(t) и у = y(t) — дифференцируемые функции независимой переменной t, то производная сложной функции z(t) = f(x(t);y(t)) вычисляется по формуле


 Таким образом, производная сложной функции (z) по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (х и у) на их производные по соответствующей независимой переменной (u и v).
Таким образом, производная сложной функции (z) по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции (z) по ее промежуточным переменным (х и у) на их производные по соответствующей независимой переменной (u и v).
44(19)
Частные производные высших порядков
Мы уже заметили, что частные производные первого порядка  мы можем рассматривать, в предположении их существования, как функции, заданные в некоторой области пространства
мы можем рассматривать, в предположении их существования, как функции, заданные в некоторой области пространства  переменных
переменных  . От каждой из этих функций
. От каждой из этих функций  , в свою очередь, можно найти частные производные:
, в свою очередь, можно найти частные производные: 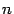 производных от
производных от  :
: 
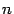 производных от
производных от 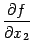 :
: 
и так далее до  ; всего получается
; всего получается  производных
производных 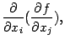 где
где  . Производная
. Производная 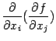 обозначается также
обозначается также  или
или 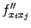 . Эти производные называются частными производными второго порядка от функции
. Эти производные называются частными производными второго порядка от функции  .
.
Если  , то есть если второе дифференцирование ведётся по той же переменной
, то есть если второе дифференцирование ведётся по той же переменной  , что и первое, то частная производная второго порядка
, что и первое, то частная производная второго порядка  называется чистой частной производной второго порядка по переменной
называется чистой частной производной второго порядка по переменной  и более кратко обозначается
и более кратко обозначается  .
.
Если же  , то частная производная второго порядка
, то частная производная второго порядка  называется смешанной частной производной второго порядка.
называется смешанной частной производной второго порядка.
Итак, для функции  можно отыскать
можно отыскать 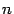 чистых частных производных второго порядка и
чистых частных производных второго порядка и  смешанных. Ниже мы увидим, что при некоторых дополнительных предположениях смешанные частные производные
смешанных. Ниже мы увидим, что при некоторых дополнительных предположениях смешанные частные производные 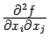 и
и  , отличающиеся порядком дифференцирований, совпадают, так что различных смешанных производных второго порядка оказывается не
, отличающиеся порядком дифференцирований, совпадают, так что различных смешанных производных второго порядка оказывается не  , а вдвое меньше.
, а вдвое меньше.
От любой из частных производных второго порядка можно рассматривать, в свою очередь, частные производные:  Эти производные (их
Эти производные (их 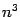 штук) называются частными производными третьего порядка; от них можно найти частные производные четвёртого порядка
штук) называются частными производными третьего порядка; от них можно найти частные производные четвёртого порядка
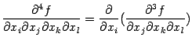
Если при вычислении частной производной высокого порядка некоторые дифференцирования проводятся по одной и той же переменной несколько раз подряд, то это отражается в обозначениях очевидным образом, например, 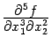 означает то же самое, что
означает то же самое, что 






