Разделение в диагностическом пространстве

Ранее рассматривались линейные разделяющие функции. Во многих случаях можно получить эффективное разделение (рас­познавание), используя разделяющие функции более сложного вида.

Разделяющая функция общего вида и диагностическое про­странство. Рассматривается распознавание образов двух классов (диагнозов D₁ и D₂)с помощью разделяющей функции общего вида

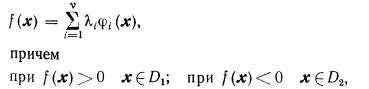
где х — вектор, изображающий объект в пространстве признаков.

Построение разделяющей функции.

Разделяющая функция будет построена, если определены коэффициенты X_t. Эти коэффи­циенты могут быть найдены в процессе обучения с помощью показа образцов из обучающей последовательности. Наиболее простой способ — использование алгоритмов для линейной разделяющей функции в диагностическом пространстве.

Использование диагностических комплексов (симптомов). Один из важных способов преобразования пространства признаков в ди­агностическое пространство — использование логических функ­ций. Очень часто диагностическое значение имеет не наличие или отсутствие какого-либо признака, а появление или непоявле­ние некоторого комплекса признаков.

Метод трубок дает некоторые правила, с помощью которых можно образовать диагностически ценные комплексы признаков. Объект описывается простыми признаками х₁ х₂,..., х_п и представляет собой одну из вершин n-мерного единичного куба, 1 —наличие признака, 0 — отсутствие признака. Различаются два состояния D₁ и D₂. Для образования характерного для каждого состояния комплекса признаков исполь­зуются объекты из обучающих последовательностей.

Если х₀ — некоторый объект (точка в пространстве призна­ков), то трубкой c центром в точке х₀ и ради­усом r называется множество точек, для которых расстояние до центра

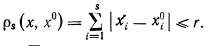
Признаки считаются существенными, если частота их появления

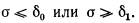
В практических расчетах можно принимать б₀ = 0,3 и б₁ = 0,7.

Процесс распознавания состоит в построении трубок. В трубку могут входить объекты, имеющие комплекс определенных признаков, находящийся в «окрестности» центра трубки.

Трубка называется чистой, если в нее входят некоторые из объектов данного состояния и не входят объекты другого состоя­ния. Предъявленный для распознавания объект относится к со­стоянию D₁ если он входит в трубки состояния D₁ и не входит в трубки состояния D₂.

В настоящее время достаточно эффективные общие процедуры отыскания диагностически цен­ных комплексов отсутствуют, однако часто инженерные и интуи­тивные соображения, особенно в задачах технической диагностики, помогают найти диагностически ценные комп­лексы и существенно снизить размерность диагностического про­странства. Отметим также методы теории подобия, позволяющие образовывать безразмерные комплексы признаков.

1. МЕТОД ПОТЕНЦИАЛЬНЫХ ФУНКЦИЙ И МЕТОД ПОТЕНЦИАЛОВ

Метод потенциальных функций является развитием идеи преобразования пространства признаков. В настоящее время метод потенциальных функций можно считать одним из наиболее разработанных и математически обоснованных методов распоз­навания образов (классов, диагнозов, состояний).

Основы метода потенциальных функций и метода потенциалов. В качестве дискриминантных функций f(х) для диагноза D₁ в пространстве признаков в рассматриваемых методах выбираются функции, имеющие наибольшее значение для точек этой области и убывающие по мере удаления от нее. Подобным свойством обла­дает потенциал точечного заряда, что и дало название методам.

Метод потенциальных функций развит для разделения на два состояния (дифференциальная диагностика, дихотомия).

Диагнозы (классы) D_l и D₂ считаются непересекающимися, т. е. точка х может входить только в один из указанных классов. Если известна потенциальная функция К (х, у), которую условно можно рассматривать как «потенциал» в точке х от источника в точке у, то при соответствующем выборе точек х₁ и х₂ можно построить разделяющую функцию. Потенциальная функция зависит от расстояния между точками:

К(х,у) = К(\х-у\).

Метод потенциалов. В этом методе для построения дискриминантных функций также используются потенциальные функ­ции К (х,у). Однако они получаются не в результате последова­тельной (рекуррентной) процедуры, как в методе потенциальных функций, а строятся на основе имеющейся предварительной ин­формации. Алгоритм построения является не самообучающимся, как в методе потенциальных функций, а заранее выбранным, детерминированным. Однако простота метода делает его привле­кательным для практических приложений.

По физическому смыслу представляет собой потенциал в точке х₁ от источника (заряда) в точке x₂. Другой метод образования дискриминантных функций состоит в использовании среднего значения потенциальной функции

Алгоритм распознавания является обычным при использовании дискриминантных функций.