Исследование испытания
1. Сформулировать исследовательскую задачу. Описание исследуемой генеральной совокупности.
2. Описание испытания, взятого в качестве эксперимента. Указание и обозначение всех исследуемых событий.
3. Проведение статистического эксперимента. Обоснование репрезентативности выборки. Указывается объём выборки (число испытаний в серии). Результаты могут быть зафиксированы в виде таблицы с указанием абсолютных и относительных частот появления событий в серии опытов.
4. Укажите точечные оценки вероятностей исследуемых событий и интервальные оценки вероятностей с доверительной вероятностью 0,95.
5. Выполните теоретический расчёт вероятностей исследуемых событий (если возможен). Проверьте на уровне значимости 0,05 гипотезу о совпадении теоретической вероятности с полученной оценкой.
6. Проведите повторный эксперимент (если возможен). Проверьте на уровне значимости 0,05 гипотезу о сохранении вероятностей исследуемых событий при выбранных условиях повторного эксперимента.
7. Сделайте выводы по результатам исследования.
Исследование случайной величины
1. Сформулировать исследовательскую задачу. Описание исследуемой генеральной совокупности.
2. Описание испытания, взятого в качестве эксперимента. Описание и обозначение исследуемой случайной величины, указание её типа.
3. Проведение статистического эксперимента. Обоснование репрезентативности выборки. Указывается объём выборки и статистический ряд полученной выборки.
4. Выполнить первичную обработку результатов статистического эксперимента: вариационный ряд, размах, медиана, мода, таблица частот/интервальная таблица частот, полигон/гистограмма (содержание первичной обработки данных зависит от типа случайной величины).
5. Оценить параметры распределения генеральной совокупности.
6. На уровне значимости 0,05 проверить гипотезу о форме закона распределения для исследуемой случайной величины (используя критерий Пирсона). Если случайная величина подчиняется нормальному закону распределения, то:
a. Найдите интервальную оценку математического ожидания случайной величины для доверительной вероятности 0,95;
b. Выполните теоретический расчёт математического ожидания случайной величины (если возможно) и проверьте гипотезу о совпадении математического ожидания с теоретическим значением на уровне значимости 0,05.
c. Выполните повторный статистический эксперимент и проверьте гипотезу о сохранении значения математического ожидания при выбранных условиях повторного эксперимента на уровне значимости 0,05.
7. Сделайте выводы по результатам исследования.
Исследование взаимосвязи случайных величин
1. Сформулировать исследовательскую задачу. Описание исследуемой генеральной совокупности.
2. Описание испытания, взятого в качестве эксперимента. Описание и обозначение исследуемых случайных величин, указание их типов.
3. Проведение статистического эксперимента. Обоснование репрезентативности выборки. Указывается объём выборки и статистический ряд выборки пар значений случайных величин.
4. Оценивается степень взаимосвязи случайных величин: вычисляется выборочный коэффициент вариации и даётся оценка степени взаимосвязи случайных величин.
5. Для линейной или сильной взаимосвязи составляется уравнение линейной регрессии, строится корреляционное поле и линия регрессии.
6. Сделайте вывод по результатам исследования.
Примечание:
Данные планы исследования являются приближёнными. Деление на пункты и порядок действий условный, совершаемые действия должны соответствовать логике исследования и поставленной задаче. По окончанию работы делается обоснованный (конкретными ссылками на полученные результаты) вывод относительно свойств исследуемого объекта. Исследование может комбинировать в себе элементы различных исследований (например, исследование по плану №3 может включать в себя исследование каждой случайной величины по плану №2).
Возможные объекты исследования:
1. Бросание монеты, бросание игральной кости, бросание несимметричного тела
2. Число очков, выпавших на игральной кости, дальность броска комка бумаги, число выпавших орлов в серии бросков монеты, дальность прыжка в длину с места.
3. Рост, вес и возраст людей в данной группе, артериальное и венозное давление человека в течение дня, число очков, выпавших на одной игральной кости, и число очков, выпавших на двух игральных костях.
Рекомендации к выполнению:
Объект исследования может быть выбран как из предлагаемого набора, так и самостоятельно. Рекомендуется выбирать объект исследования непосредственно связанный с вашей профессиональной деятельностью. При этом вы можете использовать те приёмы и методы статистических исследований, которые применяются в вашей работе. Теоретическое описание метода и его назначения необходимо включить в качестве приложения к работе.
Выводы по работе должны представлять собой интерпретацию полученных результатов исследования (выводы делаются не последовательно по пунктам, а общие выводы в конце).
Если исследования выполняются совместно несколькими студентами, то сдаётся один отчёт, в котором указываются все выполнявшие исследования (возможно, с указанием в процентах вклада каждого участника). Работы, содержащие признаки плагиата, не оцениваются.
Критерии оценки:
При оценивании работы учитывается следующее.
Выбранный объект исследования, точность и практическая значимость сформулированной исследовательской задачи. Учитывается также оригинальность выбранного исследования и связь с собственной профессиональной деятельностью.
Объём выборки должен соответствовать исследовательской задаче и не быть слишком малым (чем больше объём выборки, тем лучше).
Полнота, логичность, точность выполненных расчётов при обработке экспериментальных данных и теоретических заключений.
Обоснованность, логичность и точность сделанных выводов.
Допускается комбинирование содержания планов исследований для полноты и многогранности проводимых исследований.
Возможно выполнение нескольких статистических исследований (каждое исследование будет оцениваться отдельно).
Примеры
В этом разделе приведены примеры выполнения практических заданий. Необходимые теоретические пояснения вынесены в примечания. Примеры не являются образцами для оформления, оформление может быть иным, главное, чтобы оно было логичным и понятным, а не требовало дополнительных пояснений.
№1
Цель работы: исследовать генератор случайных чисел табличного процессора Excel.
Испытание: вычисление функции, выдающей случайное целое число из промежутка [0, 9].
А – выдано чётное число.
В – выдано число меньше 5.
С – выдано число 9.
Испытание проводится без создания особых условий вычисления, количество испытаний даёт теоретическую возможность появления каждого элементарного события несколько раз, поэтому можно считать выборку репрезентативной.
Примечание: это обоснование действует только в данном исследовании, в каждом конкретном случае обоснование зависит от конкретного исследования.
n=100
| Элементарное событие | ni |
| «0» | |
| «1» | |
| «2» | |
| «3» | |
| «4» | |
| «5» | |
| «6» | |
| «7» | |
| «8» | |
| «9» |
| Событие | ni | µi |
| А | 0,46 | |
| В | 0,52 | |
| С | 0,10 |
γ=0,95 Ф (tγ)= 0,95/2 tγ=1,96
Примечание: для вычислений используются приближённые формулы для границ доверительного интервала, т.к. число испытаний в серии велико; значение параметра t находится по таблице значений функции 
.
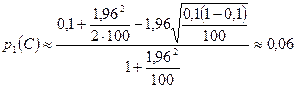
с вероятностью 0,95.
с вероятностью 0,95.
с вероятностью 0,95.
Примечание: следующее предположение определяется конкретной ситуацией, в каждом конкретном случае обоснование для вычисления теоретических вероятностей будет своё.
Исходя из общих соображений и полученных результатов, предположим, что функция выдаёт числа, подчиняющиеся равномерному распределению, т.е. все элементарные события в данном испытании равновозможны. Тогда на основании классического определения вероятности события вычисляем вероятности рассматриваемых событий:
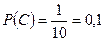
Примечание: формулируем проверяемую гипотезу, указываем уровень значимости, формулируем альтернативную гипотезу, указываем вид критической области, вычисляем значение критерия, находим область принятия гипотезы и по их соотношению значению делаем вывод о справедливости гипотез.
Н01: вероятность появления чётного числа равна 0,5.
Н02: вероятность появления числа меньшего 5 равна 0,5.
Н03: вероятность появления числа 9 равна 0,1.
α=0,05
Н11: вероятность появления чётного числа не равна 0,5.
Н12: вероятность появления числа меньшего 5 не равна 0,5.
Н13: вероятность появления числа 9 не равна 0,1.
Критическая область двухсторонняя.
Неравенство 
выполняется, поэтому данный эксперимент позволяет принять гипотезу о равенстве вероятности появления чётного числа 0,5.
Неравенство 
выполняется, поэтому данный эксперимент позволяет принять гипотезу о равенстве вероятности появления числа меньшего пяти 0,5.
Неравенство 
выполняется, поэтому данный эксперимент позволяет принять гипотезу о равенстве вероятности появления числа девять 0,1.
Н01: вероятность появления чётного числа не меняется с течением времени.
Н02: вероятность появления числа меньшего 5 не меняется с течением времени.
Н03: вероятность появления числа 9 не меняется с течением времени.
α=0,05
Н11: вероятность появления чётного числа меняется с течением времени.
Н12: вероятность появления числа меньшего 5 меняется с течением времени.
Н13: вероятность появления числа 9 меняется с течением времени.
Критическая область двухсторонняя.
Проводим повторный эксперимент:
n'=100
| Элементарное событие | ni |
| «0» | |
| «1» | |
| «2» | |
| «3» | |
| «4» | |
| «5» | |
| «6» | |
| «7» | |
| «8» | |
| «9» |
| Событие | n'i | µ'i |
| А | 0,50 | |
| В | 0,55 | |
| С | 0,07 |
Неравенство 
выполняется, поэтому данный эксперимент позволяет принять гипотезу о неизменности вероятности появления чётного числа в качестве значения функции.
Неравенство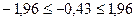 
выполняется, поэтому данный эксперимент позволяет принять гипотезу о неизменности вероятности появления числа меньшего 5 в качестве значения функции.
Неравенство 
выполняется, поэтому данный эксперимент позволяет принять гипотезу о неизменности вероятности появления числа 9 в качестве значения функции.
Примечание: содержание вывода определяется целью исследования и полученными результатами.
Вывод:
Проведённое исследование генератора случайных чисел Excel подтверждает сделанное в ходе работы предположение о том, что выдаваемые им значения функции имеют равномерное распределение на заданном множестве значений. В пользу этого говорят следующие факты. Совпадение экспериментальных данных с теоретическими вероятностями событий, найденными в предположении о равномерном распределении значений случайной функции. Кроме того, полученные точечные (при их округлении до соответствующего порядка) и интервальные оценки вероятностей рассматриваемых событий совпадают с теоретическими (теоретические значения попали в интервалы, нахождение вероятности событий в которых составляет 95%). Также было установлено (с вероятностью ошибки 5%), что вероятности исследуемых событий не меняются от опыта к опыту, что позволяет предположить справедливость данного факта по отношению к любым событиям, происходящем в результате запуска генератора случайных чисел.
№2
Цель работы: исследовать генератор случайных чисел табличного процессора Excel.
Испытание: вычисление функции, выдающей случайное целое число из промежутка [0, 9].
Х – выданное значение случайной функции.
Исследуемая случайная величина является дискретной случайной величиной с небольшим числом значений.
Испытание проводится без создания особых условий вычисления, количество испытаний даёт теоретическую возможность появления каждого значения случайной величины несколько раз, поэтому можно считать выборку репрезентативной.
n=100
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2,
2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4,
4, 4, 5, 5, 5, 5, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7,
7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9.
Вариационный ряд: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
R=9–0=9
Ме=4
Мо=1
| αi | μi |
| 0,10 | |
| 0,14 | |
| 0,06 | |
| 0,11 | |
| 0,11 | |
| 0,09 | |
| 0,11 | |
| 0,10 | |
| 0,08 | |
| 0,10 |
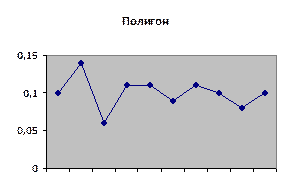
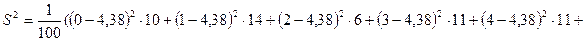
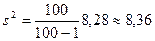
Н0: случайная величина имеет равномерное распределение на отрезке [0, 9].
α=0,05
Н1: случайная величина подчиняется иному закону распределения.
| xi | ni | n'i | 
|
| 1,6 | |||
| 1,6 | |||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
| 0,1 | |||
| 0,4 | |||
| χ2набл= |
Примечание: теоретические значения вычислены в предположении, что распределение случайной величины подчиняется равномерному закону, для других распределений и других объёмов выборки значения теоретических частот будут иными.
к=10 – 3 =7
χ2кр=14,1
Т.к. χ2набл<χ2кр, то экспериментальные данные позволяют принять гипотезу о равномерном распределении случайной величины.
Вывод:
Проведённое исследование генератора случайных чисел табличного процессора Excel показало, что значение случайной функции имеет равномерное распределение на заданном промежутке. Среднее значение случайной величины незначительно отличается от медианы, что говорит о представительности выборки.
