ТЕМА 1. НОРМИРОВАННЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА. СХОДИМОСТЬ
Основные понятия: векторное пространство, норма, нормированное векторное пространство, cходимость последовательностей по норме, сходимость в пространствах.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
а) Задает ли норму в пространстве R функция  ?
?
б) Показать, что  в пространстве
в пространстве 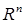 не является нормой при
не является нормой при  и
и  .
.
Решение. а) Нет, не задает, ибо не выполняется вторая аксиома нормы. Действительно, если взять 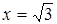 ,
, 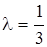 , то
, то  , а
, а  . Поэтому
. Поэтому 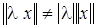 .
.
б) Не является, т.к. не выполняется третья аксиома нормы. Действительно, возьмем вектор  и вектор
и вектор 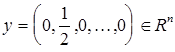 . Тогда
. Тогда  для любого
для любого  и
и  . Однако
. Однако 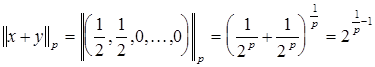 . Поскольку
. Поскольку  , то
, то 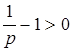 и
и  . Следовательно,
. Следовательно,  .
.
Задача № 2. Найти предел последовательности  в пространстве C [0,2], если он существует.
в пространстве C [0,2], если он существует.
Решение: Необходимым условием сходимости последовательности в пространстве C [ a,b ] является существование предела xn при каждом фиксированном 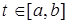 . Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна.
. Заданная последовательность при заданном t сходится к функции a(t)=t. Данная функция непрерывна.
Проверим, сходится ли последовательность xn к a(t) по норме пространства C [ a,b ], т.е. равномерно. Вычислим  . По определению нормы:
. По определению нормы:
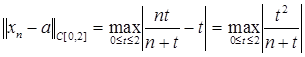 .
.
Вычислим максимум функции  на отрезке [0,2]. Для этого вычислим точки, подозрительные на экстремум с помощью производной.
на отрезке [0,2]. Для этого вычислим точки, подозрительные на экстремум с помощью производной.

Таким образом, точками, подозрительными на экстремум, являются точки  . Поскольку
. Поскольку  , поэтому остается лишь точка
, поэтому остается лишь точка  . Вычислим также значение функции на концах отрезка:
. Вычислим также значение функции на концах отрезка:
 . Значит,
. Значит,  .
.
Это означает, что последовательность  в пространстве C [0,2] сходится к функции a(t)=t.
в пространстве C [0,2] сходится к функции a(t)=t.
Задача № 3. Найти предел последовательности  в пространстве C [0,1], если он существует.
в пространстве C [0,1], если он существует.
Решение. Последовательность  для каждого фиксированного t при
для каждого фиксированного t при  стремится к a(t)= 0. Покажем, что
стремится к a(t)= 0. Покажем, что  к нулю равномерно не сходится. Вычислим
к нулю равномерно не сходится. Вычислим  .
.
Так как  , то
, то  , если
, если  .
.
Точкой, подозрительной на экстремум, является и точка  . Непосредственной проверкой убеждаемся, что максимум достигается в точке
. Непосредственной проверкой убеждаемся, что максимум достигается в точке  . Поэтому
. Поэтому  .
.
Значит, последовательность 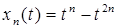 в пространстве C [0,1] не сходится.
в пространстве C [0,1] не сходится.
Задача № 4. Выяснить, сходится ли последовательность  в пространстве
в пространстве 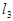 .
.
Решение. Необходимым условием сходимости последовательности в пространстве 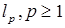 является наличие покоординатного предела. Выпишем несколько членов последовательности:
является наличие покоординатного предела. Выпишем несколько членов последовательности: 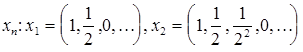 . Очевидно, что
. Очевидно, что  при
при  ,
, 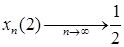 и т.д. Поэтому последовательность
и т.д. Поэтому последовательность 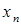 покоординатно сходится к точке
покоординатно сходится к точке  .
.
Заметим, что 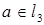 , т.к.
, т.к. 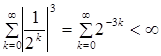 .
.
Покажем, что последовательность 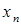 сходится к a по норме пространства
сходится к a по норме пространства  :
:
 при
при  .
.
Следовательно,  .
.
Задача № 5. Выяснить, сходится ли последовательность  в прастранстве
в прастранстве  .
.
Решение. Очевидно, что  является покоординатным пределом последовательности, но
является покоординатным пределом последовательности, но  , т.к. ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность
, т.к. ряд, составленный из единиц, не является сходящимся. Следовательно, последовательность  не имеет предела.
не имеет предела.
Задача № 6. Доказать, что последовательность  сходится поточечно к функции
сходится поточечно к функции  для всех
для всех  , но не сходится в пространстве
, но не сходится в пространстве  .
.
Решение. Последовательность  при каждом фиксированном
при каждом фиксированном  стремится к нулю, так как
стремится к нулю, так как  .
.
Вычислим 
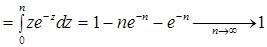 . Значит, последовательность
. Значит, последовательность  не сходится в пространстве
не сходится в пространстве  .
.
Задание №1. Можно ли в пространстве дважды непрерывно-дифференцируемых функций  на отрезке [a,b] принять за норму величину:
на отрезке [a,b] принять за норму величину:
1.1. 
1.2. 
1.3. 
1.4. 
Можно ли в пространстве непрерывно-дифференцируемых функций  на отрезке [a,b] принять за норму величину:
на отрезке [a,b] принять за норму величину:
1.5.  ;
;
1.6. 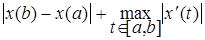 ;
;
1.7.  ;
;
1.8.  ;
;
Найти условия, при которых функция 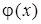 в пространстве l2 определяет норму
в пространстве l2 определяет норму
1.9.  ;
;
1.10  - фиксировано;
- фиксировано;
Определить, задает ли пара 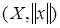 нормированное векторное пространство:
нормированное векторное пространство:
1.11. 
1.12. 
1.13. 
1.14. 
1.15.  .
.
Задание №2. Найти предел последовательности  в нормированном векторном пространстве
в нормированном векторном пространстве  , если он существует.
, если он существует.
2.1. 
2.2. 
2.3. 
2.4. 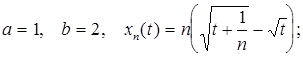
2.5. 
2.6. 
2.7. 
2.8. 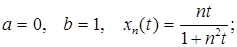
2.9. 
2.10. 
2.11. 
2.12. 
2.13. 
2.14. 
2.15. 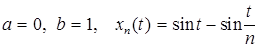 .
.
Задание №3. Найти предел последовательности  в нормированном пространстве
в нормированном пространстве  , если он существует.
, если он существует.
3.1. 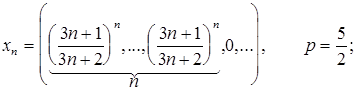
3.2. 
3.3. 
3.4. 
3.5. 
3.6. 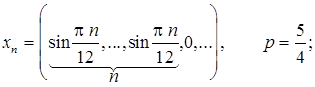
3.7. 
3.8. 
3.9. 
3.10. 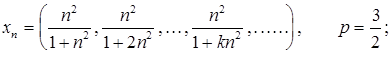
3.11. 
3.12. 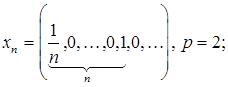
3.13. 
3.14. 
3.15.  .
.
ТЕМА 2. ГЕОМЕТРИЯ И ТОПОЛОГИЯ НОРМИРОВАННОГО ВЕКТОРНОГО ПРОСТРАНСТВА
Основные понятия: нормированное векторное пространство, сходимость последовательностей по норме, открытое, замкнутое, ограниченное, выпуклое множество в нормированном пространстве, точка прикосновения, предельная, изолированная, внутренняя, внешняя и граничная точки множества, топология нормированного векторного пространства.
Примеры решениЯ задаЧ.
Задача № 1. Является ли множество 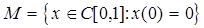 открытым, замкнутым, в пространствах
открытым, замкнутым, в пространствах  . Найти его замыкание, внутренние и граничные точки в каждом из указанных пространств.
. Найти его замыкание, внутренние и граничные точки в каждом из указанных пространств.
Решение. Докажем, что множество M не является открытым в пространстве C [0,1]. Рассмотрим точку  , т.е.
, т.е.  и x (0)=0. Для каждого
и x (0)=0. Для каждого  существует функция
существует функция  ,
,  такая, что
такая, что  , как только
, как только  . Функция x(t) принадлежит шару
. Функция x(t) принадлежит шару  , но не принадлежит множеству M. Таким образом, у мнoжества M нет внутренних точек и M не является открытым.
, но не принадлежит множеству M. Таким образом, у мнoжества M нет внутренних точек и M не является открытым.
Проверим, является ли множество M замкнутым в C [ a,b ]. Напомним, что  , если из того, что
, если из того, что  и
и  следует, что
следует, что  . Другими словами, M замкнуто, если для каждой последовательности непрерывных функций таких, что
. Другими словами, M замкнуто, если для каждой последовательности непрерывных функций таких, что  и для которых существует непрерывная на отрезке [0,1] функция
и для которых существует непрерывная на отрезке [0,1] функция  такая, что
такая, что  при
при  , функция
, функция  удовлетворяет условию
удовлетворяет условию  . Учитывая, что сходимость в пространстве C [0,1] равномерная, то из того, что
. Учитывая, что сходимость в пространстве C [0,1] равномерная, то из того, что  при
при  следует
следует  при
при  для всех
для всех  . Следовательно,
. Следовательно, 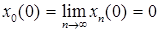 . Итак, в пространстве C [a,b] множество M замкнуто и каждая его точка для множества M является граничной.
. Итак, в пространстве C [a,b] множество M замкнуто и каждая его точка для множества M является граничной.
Каждый открытый шар радиуса r в пространстве CL [ a,b ] содержит открытый шар радиуса 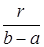 пространства C [a,b] с центром в той же точке, т.е.
пространства C [a,b] с центром в той же точке, т.е.  . Действительно, пусть
. Действительно, пусть  , т.е.
, т.е.  , тогда
, тогда 
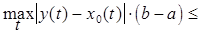
 , т.е.
, т.е.  . Значит, если множество открыто в пространстве CL [0,1], то оно открыто в C [0,1]. А так как множество M не является открытым в C [ a,b ], то оно не является открытым и в CL [ a,b ].
. Значит, если множество открыто в пространстве CL [0,1], то оно открыто в C [0,1]. А так как множество M не является открытым в C [ a,b ], то оно не является открытым и в CL [ a,b ].
Докажем, что оно не является замкнутым в CL [ a,b ], точнее,  . Действительно, для каждой функции
. Действительно, для каждой функции 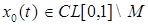 существует последовательность
существует последовательность  такая, что
такая, что  , где
, где  и
и  ,
,
 , однако
, однако 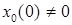 , что и означает незамкнутость множества.
, что и означает незамкнутость множества.
Задача № 2. Выяснить, является ли множество  открытым, замкнутым, ограниченным в пространстве
открытым, замкнутым, ограниченным в пространстве  .
.
Решение. Рассмотрим последовательность 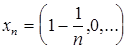 , принадлежащую множеству M, которая сходится в
, принадлежащую множеству M, которая сходится в  к элементу
к элементу 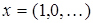 , который множеству M не принадлежит. Значит, M не является замкнутым.
, который множеству M не принадлежит. Значит, M не является замкнутым.
Докажем, что M не является также открытым, т.е. существует такая точка  , что
, что  существует точка
существует точка 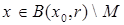 . Пусть
. Пусть  . Ряд
. Ряд  сходится, обозначим его сумму через
сходится, обозначим его сумму через  и рассмотрим последовательность
и рассмотрим последовательность  ,
,  , т.к.
, т.к.  .
.
Но  , так как
, так как  .
.
Ряд  расходится, т.е.
расходится, т.е. 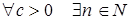 , что
, что  . Если в качестве c взять
. Если в качестве c взять  , то получим, что
, то получим, что  , что
, что  , т.е.
, т.е.  . Значит, M не является открытым. Множество M является ограниченным, так как оно содержится в шаре
. Значит, M не является открытым. Множество M является ограниченным, так как оно содержится в шаре  , где
, где  . Действительно, из условия
. Действительно, из условия 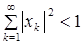 следует, что
следует, что 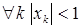 , но тогда
, но тогда  и
и  .
.
Задача № 3. Доказать, что  является подпространством пространства
является подпространством пространства  .
.
Решение. Подпространством называется замкнутое линейное многообразие. Пусть 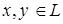 и
и  , тогда
, тогда  , т.к.
, т.к. 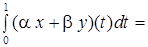
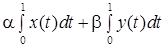 .
.
Покажем, что множество L замкнуто. Пусть  и
и  , тогда
, тогда  . Действительно, если
. Действительно, если  , то
, то
 т.к.
т.к. 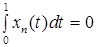 .
.
Значит, L - подпространство в СL [0,1].
Задача № 4. Доказать, что множество  нигде не плотно в l2.
нигде не плотно в l2.
Решение. По определению множество A является нигде не плотным в нормированном векторном пространстве, если оно не плотно ни в одном шаре, т.е. если в каждом шаре  содержится другой шар
содержится другой шар  , не имеющий с A ни одной общей точки.
, не имеющий с A ни одной общей точки.
Пусть  - произвольный шар в
- произвольный шар в  . Возможны два варианта:
. Возможны два варианта:
1)  ;
;
2)  .
.
Во втором случае рассмотрим шар 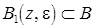 и точку
и точку  . Тогда для
. Тогда для  имеем:
имеем:  , т.е.
, т.е.  , кроме того
, кроме того  . Таким образом, в шаре
. Таким образом, в шаре  всегда найдется шар
всегда найдется шар 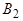 , не содержащий точек множества
, не содержащий точек множества 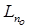 , т.е.
, т.е. 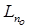 нигде не плотно.
нигде не плотно.
Задача № 5. Доказать, что множество 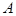 последовательностей из
последовательностей из  , содержащих лишь конечное число членов, отличных от нуля, плотно в
, содержащих лишь конечное число членов, отличных от нуля, плотно в  .
.
Решение. Пусть  , т.е.
, т.е. 


 :
: 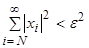 . Обозначим через
. Обозначим через  . Очевидно,
. Очевидно,  и
и  . Значит,
. Значит,  является точкой прикосновения для множества
является точкой прикосновения для множества 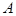 , следовательно
, следовательно 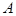 всюду плотно в
всюду плотно в  .
.
Задание №1. Определите, является ли данное множество замкнутым, открытым в пространстве  . Найдите его замыкание, внутренние и граничные точки в каждом указанном пространстве.
. Найдите его замыкание, внутренние и граничные точки в каждом указанном пространстве.
1.1. 
1.2. 
1.3. 
1.4. 
1.5. 
1.6. 
1.7. 
1.8. 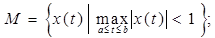
1.9. 
1.10. 
1.11. 
1.12. 
1.13.  .
.
Задание 2. Для данного множества M выяснить,является ли множество  открытым, замкнутым, ограниченным в lp.
открытым, замкнутым, ограниченным в lp.
2.1. 
2.2. 
2.3. 
2.4. 
2.5. 
2.6. 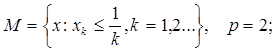
2.7. 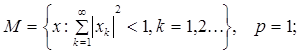
2.8. 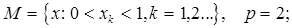
2.9. 
2.10. 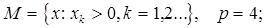
2.11. 
2.12. 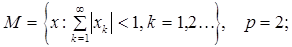
2.13. 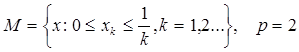
2.14. 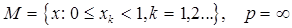 .
.






