Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г.
Вариант № 7
Задача 1
Найти множество сходимости функционального ряда  .
.
Задача 2
В прямоугольной системе координат Oxy линия задана уравнением:


Найти каноническую прямоугольную систему координат и каноническое уравнение линии.
Задача 3
Написать программу для решения следующей задачи. Дано 30 различных чисел.
Напечатать их по убыванию.
Задача 4
Решить задачу

Задача 5
Построить совершенную дизъюнктивную нормальную форму для функции алгебры логики

Задача 6
Решить задачу линейного программирования 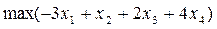
При ограничениях 
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11»__ мая __2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г. 
Вариант № 8
Задача 1
Разложить функцию y=x в тригонометрический ряд Фурье на интервале 
Задача 2
Найти матрицу  если
если 
Проверить правильность ответа, пользуясь определением обратной матрицы.
Задача 3
Написать программу для решения следующей задачи. Имеется непустая последовательность букв, за которой следует точка. Напечатать эту же последовательность, удалив из нее все буквы U, непосредственно перед которыми находится буква Q.
Задача 4
Решить задачу Коши

Задача 5
Записать формулу вычисления интеграла.

По методу Симпсона с числом узлов 2N+1 и дать оценку погрешности (N=100).
Задача 6
Плотность распределения случайной величины  равна
равна

Найти: a) постоянную A; б) функцию распределения F(x); в) вероятность того, что величина  попадает на отрезок
попадает на отрезок 
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11»__ мая __2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г. 
Вариант № 9
Задача 1
Определить наибольшее и наименьшее значение функции

В прямоугольнике 
Задача 2
Найти точку, симметричную точке (3,2,1) и относительно прямой
x = 1 + 2t, y = 1 + t, z = 1 + 2t.
Система координат прямоугольная.
Задача 3
Написать программу для решения следующей задачи. Имеется непустая последовательность целых чисел величиной от 1 до 40, за которой следует 0.
Напечатать все числа, входящие в эту последовательность более трех раз.
Задача 4
Решить задачу

Задача 5
Выяснить, полна ли система  функций алгебры логики
функций алгебры логики

Задача 6
Среди дважды непрерывно дифференцируемых функций y = y(x), заданных на отрезке [-1;1] и удовлетворяющих краевым условиям

есть функция, доставляющая минимум функционалу

Найти эту функцию.
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11»__ мая __2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________






