МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г.
Вариант № 1
Задача 1
Вычислить площадь области ограниченной кривой
.
Задача 2
Определить, является ли линейно независимой система векторов
(2,1,-2,3); (0,2,0,1); (1,0,1,1); (0,2,1,-1).
Если она линейно независима, то вектор (0,0,0,1) представить в виде ее линейной комбинации. В противном случае один из векторов системы представить в виде линейной комбинации остальных трех.
Задача 3
Написать программу для решения следующей задачи. Дано 100 различных чисел.
Найти наибольшее из них.
Задача 4
Найти общее решение уравнения
Задача 5
Используя метод касательных (Ньютона), определить с точностью до 0,01 корень α уравнения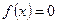 
, где 
на отрезке 
Задача 6
При каком значении a функция
для любого x является плотностью распределения случайной величины 
ξ.
Найти а) функцию распределения F(x) случайной величины ξ;
б) вероятность попадания случайной величины в интервал (-1;1)
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11»___ мая ___2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г.
Вариант № 2
Задача 1
Найти множество сходимости функционального ряда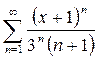 
.
Задача 2
В прямоугольной системе координат Oxy линия задана уравнением:
Найти каноническую прямоугольную систему координат и каноническое уравнение линии.
Задача 3
Написать программу для решения следующей задачи. Дано 20 различных чисел.
Напечатать их по возрастанию.
Задача 4
Решить задачу
, для любого x, a t>0,
для любого x.
Задача 5
Построить совершенную дизъюнктивную нормальную форму для функции алгебры логики
Задача 6
Решить задачу линейного программирования
при ограничениях 
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11»_ мая ___2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г.
Вариант № 3
Задача 1
Разложить функцию y= 
в тригонометрический ряд Фурье на интервале 
Задача 2
Найти матрицу 
, если
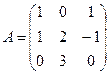
Проверить правильность ответа, пользуясь определением обратной матрицы.
Задача 3
Написать программу для решения следующей задачи. Имеется непустая последовательность букв, за которой следует точка. Напечатать эту же последовательность, заменив в ней пары букв PH на F.
Задача 4
Решить задачу Коши
, 
Задача 5
Записать формулу вычисления интеграла
По методу Симпсона с числом узлов 2N+1 и дать оценку погрешности (N=100).
Задача 6
Плотность распределения случайной величины 
имеет вид
Найти: a) значение параметра A;
б) функцию распределения F(x) случайной величины ;
в) вероятность попадания случайной величины на отрезок [0;1].
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11»_ мая ___2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
