Определитель.
Определитель (детерминант) квадратной матрицы 
– это число 
, которое ставится в соответствие матрице и вычисляется по ее элементам согласно следующим правилам.
1. Определителем матрицы 
порядка 
называется единственный элемент этой матрицы: 
.
2. Определителем матрицы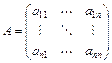 
порядка 
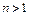называется число
, (2.1)
где 
– определитель квадратной матрицы порядка 
, полученной из вычеркиванием первой строки и 
-го столбца.
Базисный минор и ранг матрицы.
В матрице размеров 
минор 
-го порядка называется базисным, если он отличен от нуля, а все миноры 
-го порядка равны нулю или их вообще не существует.
Рангом матрицы называется порядок базисного минора.
Теорема о базисном миноре. В произвольной матрице каждый столбец (строка) является линейной комбинацией столбцов (строк), в которых расположен базисный минор.
Теорема о ранге матрицы Ранг матрицы равен максимальному числу линейно независимых строк этой матрицы.
Теорема (необходимое и достаточное равенство нулю определителя) Для того чтобы определитель был равен нулю, необходимо и достаточно, чтобы один из его столбцов (одна из его строк) был линейной комбинацией остальных столбцов (строк).
Понятия линейной зависимости и линейной независимости векторов
Вектор 
называется линейной комбинацией векторов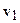 
, 
,…, 
, если 
, где 
, 
,…, 
– некоторые числа.
Система из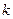 
векторов 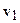, ,…, называется линейно зависимой, если существуют такие числа , ,…, не все равные нулю одновременно, что справедливо равенство 
. (*) т.е. линейная комбинация является нулевым вектором.
Система из 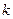векторов 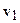, ,…, называется линейно независимой, если равенство (*) возможно только при 
.
Обратная матрица.
Пусть 
– квадратная матрица порядка 
. Матрица 
, удовлетворяющая вместе с заданной матрицей равенствам: 
, называется обратной. Если определитель матрицы равен нулю (
), то для нее не существует обратной.
Теорема о существовании и единственности обратной матрицы
Квадратная матрица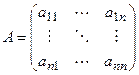 
, определитель которой отличен от нуля, имеет обратную матрицу и притом только одну, которая вычисляется по формуле: 
, где 
– матрица, транспонированная для матрицы, составленной из алгебраических дополнений элементов матрицы . Матрица 
называется присоединенной матрицей по отношению к матрице .
Системы линейных алгебраических уравнений
Правило Крамера. Если определитель 
матрицы системы линейных уравнений с неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам
, 
,
где 
– определитель матрицы, полученной из матрицы системы заменой 
-го столбца столбцом свободных членов, т.е.
.
Теорема Кронекера–Капелли. Система 
совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы: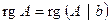 
.
Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.
Любая совокупность 
линейно независимых решений 
, 
,…, 
однородной системы называется фундаментальной системой (совокупностью) решений.
Структура общего решения неоднородной системы. Общее решение неоднородной системы есть сумма частного решения неоднородной системы и общего решения соответствующей однородной системы:
.
Собственные векторы
Пусть – квадратная матрица -го порядка. Ненулевой столбец 
, удовлетворяющий условию 
, (*)
называется собственным вектором матрицы . Число 
в равенстве (*) называется собственным значением матрицы . Говорят, что собственный вектор 
соответствует (принадлежит) собственному значению .
Характеристическое уравнение: 
.
Совокупность всех собственных значений матрицы (с учетом их кратностей) называют ее спектром. Спектр матрицы называется простым, если собственные значения матрицы попарно различные (все корни характеристического уравнения простые).
Алгоритм нахождения собственных векторов и собственных значений матрицы
Для нахождения собственных векторов и собственных значений квадратной матрицы 
-го порядка надо выполнить следующие действия.
1. Составить характеристический многочлен матрицы 
.
2. Найти все различные корни 
,…, 
характеристического уравнения 
; кратности 
, 
,…, 
(
) корней определять не нужно.
3. Для корня 
найти фундаментальную систему 
, 
,…, 
решений однородной системы уравнений 
, где 
.
4. Записать линейно независимые собственные векторы матрицы , отвечающие собственному значению : 
, 
,…, 
,
где 
, 
,…, 
– отличные от нуля произвольные постоянные. Совокупность всех собственных векторов, отвечающих собственному значению , образуют ненулевые столбцы вида 
.
Повторить п.3, 4 для остальных собственных значений 
,…, .
Теорема о приведении матрицы к диагональному виду. Для того чтобы квадратная матрица -го порядка приводилась к диагональному виду 
, необходимо и достаточно, чтобы она имела линейно независимых собственных векторов.
Следствие. Если матрица имеет простой спектр, то она приводится к диагональному виду.
Векторная алгебра.
Скалярным произведением двух ненулевых векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
,
где 
– величина угла между векторами 
и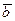 
.
Если векторы и 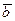относительно ортонормированного базиса в пространстве имеют координаты 
, 
, 
и 
, 
, 
соответственно, то скалярное произведение этих векторов вычисляется по формуле 
.
Ненулевые векторы и 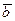ортогональны тогда и только тогда, когда 
.
Упорядоченная тройка некомпланарных векторов называется правой, если, наблюдая из конца третьего вектора, кратчайший поворот от первого вектора ко второму виден происходящим против часовой стрелки. Если описанный поворот виден происходящим по часовой стрелке, то упорядоченная тройка некомпланарных векторов называется левой тройкой.
Вектор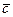 
называется векторным произведением неколлинеарных векторов и 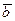, если:
1) его длина равна произведению длин векторов и 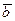на синус угла между ними: 
;
2) вектор 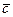ортогонален векторам и ;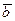
3) векторы , , 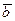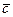(в указанном порядке) образуют правую тройку.
Формула вычисления векторного произведения. Если векторы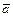 
и 
в правом ортонормированном базисе 
, 
, 
имеют координаты 
, 
, 
и 
, 
, 
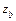соответственно, то векторное произведение этих векторов находится по формуле: 
.
Геометрические приложения векторного произведения
1. Векторы 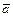и коллинеарны тогда и только тогда, когда 
.
2. Площадь 
параллелограмма, построенного на векторах 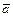и , вычисляется по формуле: 
.
3. Высота 
параллелограмма (треугольника), построенного на векторах 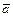, , вычисляется по формуле: 
.
Смешанным произведением векторов , , 
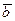называется число 
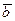, равное скалярному произведению вектора на векторное произведение векторов и 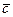. Смешанное произведение обозначается 
.
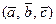Геометрические свойства смешанного произведения
1. Модуль смешанного произведения некомпланарных векторов , ,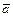 
равен объему 
параллелепипеда, построенного на этих векторах.
2. 
векторы , , 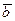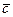компланарны.
Формула вычисления смешанного произведения.
.
