Ряд динамики – это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления.
ряд динамики можно представить в виде следующих составляющих: 1) тренд – основная тенденция развития ряда динамики к возрастанию или убыванию,2) циклические (в том числе и сезонные) колебания,3) случайные колебания.
Изучение тренда проводится в 2 этапа: - ряд динамики проверяется на наличие тренда,
- производится выравнивание временного ряда и непосредственное выделение тренда.
Методы выделения тренда1. Укрупнение интервалов. Уровни ряда заменяют уровнями, рассчитанными по более продолжительным интервалам, одновременно уменьшая их количество. 2. Скользящая средняя. Исходные уровни заменяются средними величинами, рассчитанными из данного уровня и нескольких симметрично его окружающих. То количество уровней, по которым рассчитывается средняя называют интервалом сглаживания или периодом скольжения, который может быть четным и нечетным. При нечетном сглаживании полученное среднее арифметическое значение закрепляют за серединой расчетного интервала. При четном сглаживании этого сделать нельзя. Поэтому при обработке ряда с четными интервалами их искусственно делают нечеткими, используя ближайший больший нечетный интервал, где их крайних его уровней берут 50%.
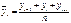
3. Аналитическое выравнивание. Определение основной, проявляющейся во времени тенденция развития изучаемого явления. В ходе выравнивания временного ряда получают аналитическую или графическую зависимость от времени.
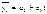- линейная;
параболическая
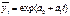- экспоненциальная
Линейная зависимость выбирается, когда в исходном временном ряду наблюдаются более или менее постоянные абсолютные цепные приросты, не проявляющие тенденции ни к увеличению, ни к снижению.
Параболическая зависимость используется, если абсолютные цепные приросты сами по себе обнаруживают некоторую тенденцию развития.
Экспоненциальная зависимость применяется, если наблюдается более или менее постоянный относительный рост.
Коэффициенты из уравнения тренда можно найти при помощи метода наименьших квадратов.
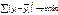
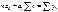
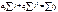
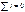
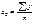- средний уровень ряда 
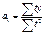1
4. Виды признаков. Связи между ними. Оценка тесноты связи
Все признаки можно классифицировать на: 1) факторные, т.е. обуславливающие изменения другого признака (х) 2) результативные, т.е. изменяющиеся под влиянием других признаков (у)
связи между признаками можно разделить по типам: - функциональная (жестко детерминированная). Каждому значению факторного признака х соответствует одно или несколько жестко определенных значений y;- статистическая. Среднее значение результативного признака зависит от изменения факторного. Частный случай статистической связи – корреляционная связь - заключается в том, что различным значениям одной переменной могут соответствовать различные значения другой переменной.
Виды связей:а) по направлению: - прямая (с увеличением х, у увеличивается и наоборот), - обратная (с увеличением х, у уменьшается и наоборот)б) по форме:- линейная (у=ах+в), - нелинейные (любая кривая)в) по степени тесноты связей: - сильная, - умеренная, - слабая, - отсутствует. г) по количеству признаков: множественные и парные
