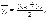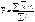Показатели вариации. Правило сложения дисперсий
Вариация – несовпадение уровней одного и того же показателя у разных объектов.
Абсолютные показатели вариации:
1. Размах вариации, R=Xmax - Xmin,
2. среднее линейное отклонение – это среднее отклонение от средней
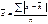(если данные не сгруппированы)
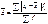(взвешенное среднее линейное отклонение)
3. дисперсия (средний квадрат отклонений от средней)
(невзвешенная формула) 
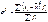(взвешенная формула)
Среднее квадратическое отклонение
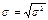
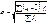- взвешенная формула
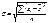- невзвешенная формула
Правило сложения дисперсий:
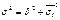, рассчитывается по всей совокупности в целом
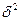- межгрупповая дисперсия, характеризует систематическую вариацию признака, зависит от признака – фактора, положенного в основу группировки
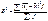
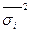- среднее из групповых дисперсий, характеризует случайную вариацию
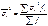
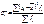
Относительные показатели вариации
Базой для сравнения в них служит ср.арифмет. Чаще всего они выражаются в % и характеризуют не только сравнительную оценку вариаций, но и однородность совокупности.
-коэффициент вариаций:
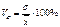если не превышает 33% совокупность считается однородной
- коэффициент осцилляции: Vr=R/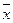 
*100%,
- линейный коэффициент вариации Vл=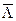 
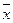/ *100%
2. Показатели анализа рядов динамики: цепные, базисные, средние
Ряд динамики – последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Классификация: 1. По времени: а) моментные ряды – это последовательность, в которой уровень явления показывает наличие изучаемого явления в конкретный момент времени. Уровни моментного ряда складывать нельзя. б) интервальные ряды – последовательность, в которой уровень ряда показывает результат накопленный или вновь произведенный за определенный промежуток времени. Уровни можно складывать. 2. По форме представления уровней: а) ряды абсолютных величин, б) ряды относительных величин, в) ряды средних величин. 3.По расстоянию между датами: а) полные ряды – с равными интервалами, б) неполные ряды – с неполными интервалами.
4. По количеству показателей: а) изолированный (только один показатель), б) комплексный (2 и более)
Показатели анализа рядов динамики:
1. Показатели интенсивности развития явления (табличка идет отдельно)
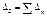- абсолютный прирост будет равен сумме абсолютных цепных приростов за рассматриваемый период.
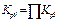- базовый коэффициент роста равен произведению цепных коэффициентов роста.
Средние показатели динамики
1. Средний абсолютный прирост:
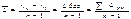
2. Средний темп роста:
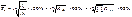
3. Средний темп прироста:
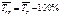
4. Средний уровень ряда:
а) для интервальных рядов:
- с равными интервалами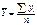 
- с неравными интервалами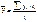 
,
б) для моментных рядов:
- с равными интервалами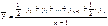 
- с неравными интервалами: сначала находятся средние за каждый интервал:
…; 
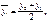
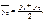