Технически более просто осуществляется адиабатный процесс расширения газа из равновесного состояния 1, при котором температура системы Т 1 равна температуре Т о окружающей внешней среды, а давление Р 1 = Р о + 
Р 1 превышает значение атмосферного давления Р о. По окончании адиабатного процесса в квазиравновесном состоянии 2 температура будет Т 2= Т о - Т, а давление в системе Р 2 = Р о.
 |
Для эксперимента необходима система, способная спонтанно увеличить свой объем при неизменном количестве вещества в нем. Такая система не может быть ограничена стенками какого-либо сосуда, имеющего постоянный объем. В то же время избыточное давление в системе можно обеспечить только тогда, когда она заключена в таком сосуде. Для устранения этого противоречия выберем систему молекул внутри сосуда, но занимающую при избыточном давлении Р 1 только небольшую часть V 1 объема сосуда, как показано на рис. 6.1, где выделенная система условно ограничена круговой линией.
В исходное равновесное состояние 1 система приходит после предварительного сжатия (подкачка газа может быть осуществлена насосом) и последующей релаксации (в течение нескольких минут), когда в условиях теплового равновесия с внешней средой весь газ в сосуде будет иметь температуру Т 1 = Т о и установившееся давление Р 1.
В процессе быстрого адиабатного расширения системы, производимого резким соеди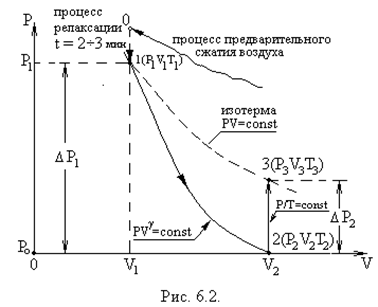 
нением через открывающийся клапан К полости сосуда с внешней средой, теплообменом газа в сосуде и, тем более, в выделенной системе, можно пренебречь (d Q ® 0). Внутренняя энергия системы уменьшается на величину 
, расходуемую на работу А расширения системы: D U ® А. На диаграмме (рис.6.2) адиабатный процесс перехода из состояния 1 в состояние 2 показан графически.
Из уравнения (6.1) адиабатного процесса для состояний 1 и 2 следует равенство 
, но так как Р 2 = Р 0, то можно записать, что 
. Отсюда найдем, что показатель адиабаты
(6.5)
В формуле (6.5)
так как
а отношение объемов V 2 / V 1, остается неизменным.
Особенностъ метода Клемана и Дезорма состоит в том, что после адиабатного процесса из состояния 2 система, сохраняя постоянный объем, изохорически в течение некоторого времени переходит в равновесное состояние 3 (см.рис.6.1), при котором в условиях теплового равновесия с внешней средой она приобретает температуру Т о этой среды: V 3 = V 2, Т 3 = Т 0 и Р 3 > Р 0. Таким образом, состояния 1 и 3 являются изотермическими (Т 1 = Т 0 и Т 3 = Т 0), т.е. принадлежат некоторой теоретической изотерме (на рис.6.2 – пунктирная линия РV = const). Поэтому для этих состояний можно записать равенство Р 1 V 1 = Р 3 V 3, либо, учитывая, что V 3 = V 2, равенство Р 1 V 1 = Р 3 V 2. Отсюда следует, что в формуле (3) неизвестное отношение объемов можно заменить отношением давлений
|
где 
- приращение давления при изохорическом процессе. Учитывая, что 
и 
получим
|
Подставляя найденные выражения для логарифмов в формулу (5) запишем в окончательном виде уравнение, позволяющее производить измерение показателя адиабаты по методу Клемана и Дезорма
| (6.6) |
Измерения с помощью формулы (6.6) - косвенные. Однако при обработке результатов измерений их следует рассматривать как прямые, в каждом эксперименте вычисляя значение g1, g2,…gi, …gn, а затем находя среднее значение 
и погрешность Dg. Эта особенность объясняется невоспроизводимостью от опыта к опыту исходного состояния 1 (Р 1, V 1, Т 1) системы, которое образуется спонтанно из неравновесного состояния 0, в значительной мере зависящего от способа и режима нагнетания воздуха в сосуд.
