27. Векторная диаграмма. Сложение параллельных колебаний одинаковой частоты.Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. 
1). Выберем некоторую направленную прямую - ось, вдоль которой будем откладывать колеблющуюся величину x. 2). Из взятой на оси некоторой точки О отложим направленный отрезок - вектор длины A, образующий с осью угол некоторый α.3). Вращая вектор А вокруг точки О с угловой скоростью ω 0 , получим, что проекция конца вектора на ось будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени: проекция конца вектора будет перемещаться по оси x, принимая значения от - А до + A, а координата этой проекции будет изменяться со временем по закону 
Схему, полученную таким методом представления колебаний, называют векторной диаграммой. Рассмотрим сложение двух гармонических колебаний х 1 и x 2 одного направления и одинаковой частоты: 
, 
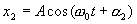(1) Оба колебания представим с помощью векторов A 1 и А 2. Используя правила сложения векторов можно найти результирующий вектор А, представляющий собой сумму двух векторов A 1 и А 2. 
Вектор A представляет собой результирующее колебание, потому что из рисунка видно, что проекция этого вектора на ось x равна сумме проекций складываемых векторов: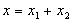 
Вектор A вращается с той же угловой скоростью ω 0 , как и векторы А1 и А2, так что сумма x 1 и х 2 является гармоническим колебанием с частотой (ω 0 , амплитудой A и начальной фазой α. Используя теорему косинусов получаем, что 
(2) 
(3) Замена сложения функций сложением векторов, которая возможна при Представление гармонических колебаний с помощью векторов, значительно упрощает вычисления.
28. Биения.Биения — явление, возникающее при наложении двух гармонических колебаний близкой частоты и выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.
Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.
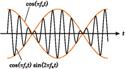
29. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу.Фигуры Лиссажу — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Ж. Лиссажу (J. Lissajous; 1822—80). Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или π вырождаются в отрезки прямых, а при разности фаз π/2 и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний. 
Сложение взаимно перпендикулярных колебаний. Рассмотрим две взаимно перпендикулярные векторные величины x и y, изменяющиеся со временем с одинаковой частотой ω по армоническому закону: 
(1)Где e x и e у — орты координатных осей x и y, А и B — амплитуды колебаний. Величинами x и у может быть, например, смещения материальной точки (частицы) из положения равновесия.В случае колеблющейся частицы величины x и y можно представить в виде: 
, 
(2)Они определяют координаты частицы на плоскости xy. Выражения (2) представляют собой заданное в параметрической форме уравнение траектории, по которой будет двигаться частица. Вид траектории зависит от разности фаз обоих колебаний.Исключив из уравнений (2) параметр t, получим уравнение траектории в обычном виде. Из первого уравнения: 
(3). Соответственно 
(4)По формуле для косинуса суммы:
, тогда 
Преобразуем это ура-ение
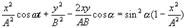
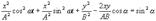
(5)
Получили уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и его полуоси зависят довольно сложным образом от амплитуд A и В и разности фаз α.
30. Статистическая физика (МКТ) и термодинамика. Состояние термодинамической системы. Равновесное, неравновесное состояния. Термодинамические параметры. Процесс. Основные положения МКТ.Термодинамическая система — это любая область пространства, ограниченная действительными или воображаемыми границами, выбранными для анализа её внутренних термодинамических параметров.Пространство, смежное с границей системы, называется внешней средой. У всех термодинамических систем есть среда, с которой может происходить обмен энергии и вещества.Границы термодинамической системы могут быть неподвижными или подвижными.Системы могут быть большими или маленькими, в зависимости от границ.Система может существовать в вакууме или может содержать несколько фаз одного или более веществ. Термодинамические системы могут содержать сухой воздух и водяной пар (два вещества) или воду и водяной пар (две стадии одного и того же вещества). Однородная система состоит из одного вещества, одной его фазы или однородной смеси нескольких компонентов.Системы бывают изолированными (замкнутыми) или открытыми. В изолированной системе не происходит никаких обменных процессов с внешней средой. В открытой системе и энергия и вещество могут переходить из системы в среду и обратно.
Состояние термодинамической системы определяется физическими свойствами вещества. Температура, давление, объем, внутренняя энергия, энтальпия и энтропия — это термодинамические величины, определяющие те или иные интегральные параметры системы. Данные параметры строго определяются лишь для систем, находящихся в состоянии термодинамического равновесия.Различают экстенсивные параметры состояния, пропорциональные массе термодинамической системы, и интенсивные параметры состояния, не зависящие от массы системы. К экстенсивным параметрам состояния. относятся: объём, Внутренняя энергия, Энтропия, Энтальпия, изохорно-изотермический потенциал Гиббсова энергия), изобарно-изометрический потенциал (Гельмгольцева энергия); к интенсивным параметрам состояния— давление, температура, концентрация, магнитная индукция и др. параметры состояния взаимосвязаны, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния. В молекулярно-кинетической теории пользуются идеализированной моделью идеального газа, согласно которой: 1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;2) между молекулами газа отсутствуют силы взаимодействия;3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов, так как они в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах близки по своим свойствам к идеальному газу.
31. Температура в термодинамике. Термометры. Температурные шкалы. Идеальный газ. Уравнение состояния идеального газа. температура(T) – это величина, характеризующая состояние термодинамического равновесия макросистем и не имеет смысла для систем, состоящих из небольшого числа частиц. Если при установлении теплового контакта между телами одно из тел передает энергию (тепло) другому, то считают, что первое тело имеет бoльшую температуру, чем второе. Термодинамическая шкала температур (шкала Кельвина) строится по одной реперной точке, так называемой тройной точке воды, в которой в состоянии равновесия могут находиться три фазы воды – твердая, жидкая и газообразная. По определению. Температура по шкале Цельсия связана с температурой по шкале Кельвина равенством 
. Температуру называют абсолютным нулем и ей соответствует t=-273.15 
. В дальнейшем мы выясним физический смысл температуры T. термометры — приборы для измерения температуры.Модель идеального газа является самой простой и вместе с тем хорошей моделью, описывающей поведение газа при не слишком низких температурах и больших давлениях. Это газ, молекулы которого не имеют собственного объема и не взаимодействуют на расстоянии. Вместе с тем взаимодействие между молекулами даже в случае идеального газа принципиально должно быть, так как только благодаря этому в системе может установиться равновесие. Можно сказать так, что идеальный газ – это газ, каждая молекула которого считает, что она одна в мире. Под уравнением состояния газа понимают уравнение, связывающее параметры газа p,V,T. Для идеального газа это уравнение имеет вид PV = n RTЕго называют уравнением Менделеева-Клапейрона.
где n – число молей газа;P – давление газа (например, в атм;V – объем газа (в литрах);
T – температура газа (в кельвинах);R – газовая постоянная (8,31Дж/(моль К))моль – это количество вещества, в котором содержится 
одинаковых частиц, молярная масса – это масса одного моля, определяемая по таблице Менделеева. Нетрудно проверить, что уравнение состояния можно также записывать в двух других эквивалентных формах: pV=NkT, p=nkT где n=N/V - концентрация частиц (число частиц в единице объема)
32. Давление газа на стенку сосуда. Закон идеального газа в МКТ. Задача молекулярно-кинетической теории состоит в том, чтобы установить связь между микроскопическими (масса, скорость, кинетическая энергия молекул) и макроскопическими параметрами (давление, газ, температура). В результате каждого столкновения между молекулами и молекул со стенкой скорости молекул могут изменяться по модулю и по направлению; на интервалах между последовательными столкновениями молекулы движутся равномерно и прямолинейно.
В модели идеального газа предполагается, что все столкновения происходят по законам упругого удара, то есть подчиняются законам механики Ньютона. Используя модель идеального газа, вычислим давление газа на стенку сосуда. В процессе взаимодействия молекулы со стенкой сосуда между ними возникают силы, подчиняющиеся третьему закону Ньютона. В результате проекция υx скорости молекулы, перпендикулярная стенке, изменяет свой знак на противоположный, а проекция υy скорости, параллельная стенке, остается неизменной. Поэтому изменение импульса молекулы будет равно 2m0υx, где m0 – масса молекулы. Выделим на стенке некоторую площадку S (рис. 3.2.2). За время Δt с этой площадкой столкнутся все молекулы, имеющие проекцию скорости υx, аправленную в сторону стенки, и находящиеся в цилиндре с основанием площади S и высотой υxΔt.
33. Температура в МКТ. Средняя энергия молекул. Среднеквадратичная скорость молекул. температура(T) – это величина, характеризующая состояние термодинамического равновесия макросистем и не имеет смысла для систем, состоящих из небольшого числа частиц. Если при установлении теплового контакта между телами одно из тел передает энергию (тепло) другому, то считают, что первое тело имеет бoльшую температуру, чем второе. Термодинамическая шкала температур (шкала Кельвина) строится по одной реперной точке, так называемой тройной точке воды, в которой в состоянии равновесия могут находиться три фазы воды – твердая, жидкая и газообразная. По определению. Температура по шкале Цельсия связана с температурой по шкале Кельвина равенством 
. Температуру называют абсолютным нулем и ей соответствует t=-273.15 
. В дальнейшем мы выясним физический смысл температуры T.Уравнение среднеквадратичной скорости молекулы легко выводится из основного уравнения МКТ для одного моля газа.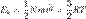 
, для 1 моля N = Na, где Na — постоянная Авогадро Nam = Mr, где Mr — молярная масса газа, Отсюда окончательно 
Тепловое равновесие – это такое состояние системы тел, находящихся в тепловом контакте, при котором не происходит теплопередачи от одного тела к другому, и все макроскопические параметры тел остаются неизменными. Температура – это физический параметр, одинаковый для всех тел, находящихся в тепловом равновесии. Возможность введения понятия температуры следует из опыта и носит название нулевого закона термодинамики.Для измерения температуры используются физические приборы – термометры, в которых о величине температуры судят по изменению какого-либо физического параметра. Для создания термометра необходимо выбрать термометрическое вещество (например, ртуть, спирт) и термометрическую величину.Термометры должны быть откалиброваны. По температурной шкале Цельсия точке плавления льда приписывается температура 0 °С, а точке кипения воды – 100 °С. Изменение длины столба жидкости в капиллярах термометра на одну сотую длины между отметками 0 °С и 100 °С принимается равным 1 °С. В ряде стран (США) широко используется шкала Фаренгейта (T F), в которой температура замерзающей воды принимается равной 32 °F, а температура кипения воды равной 212 °F. Следовательно, 
|
Особое место в физике занимают газовые термометры в которых термометрическим веществом является разреженный газ (гелий, воздух) в сосуде неизменного объема (V = const), а термометрической величиной – давление газа p. Опыт показывает, что давление газа (при V = const) растет с ростом температуры, измеренной по шкале Цельсия.
Чтобы проградуировать газовый термометр постоянного объема, можно измерить давление при двух значениях температуры (например, 0 °C и 100 °C), нанести точки p 0 и p 100 на график, а затем провести между ними прямую линию (рис. 3.2.5). Используя полученный таким образом калибровочный график, можно определять температуры, соответствующие другим значениям давления. Экстраполируя график в область низких давлений, можно определить некоторую «гипотетическую» температуру, при которой давление газа стало бы равным нулю. Опыт показывает, что эта температура равна –273,15 °С и не зависит от свойств газа. На опыте получить путем охлаждения газ в состоянии с нулевым давлением невозможно, так как при очень низких температурах все газы переходят в жидкое или твердое состояние.
Английский физик У. Кельвин (Томсон) в 1848 г. предложил использовать точку нулевого давления газа для построения новой температурной шкалы (шкала Кельвина). В этой шкале единица измерения температуры такая же, как и в шкале Цельсия, но нулевая точка сдвинута:
| T К = T С + 273,15. |
В системе СИ принято единицу измерения температуры по шкале Кельвина Например, комнатная температура T С = 20 °С по шкале Кельвина равна T К = 293,15 К.
Температурная шкала Кельвина называется абсолютной шкалой температур. Она оказывается наиболее удобной при построении физических теорий.
Нет необходимости привязывать шкалу Кельвина к двум фиксированным точкам – точке плавления льда и точке кипения воды при нормальном атмосферном давлении, как это принято в шкале Цельсия.
Кроме точки нулевого давления газа, которая называется абсолютным нулем температуры, достаточно принять еще одну фиксированную опорную точку. В шкале Кельвина в качестве такой точки используется температура тройной точки воды (0,01 °С), в которой в тепловом равновесии находятся все три фазы – лед, вода и пар. По шкале Кельвина температура тройной точки принимается равной 273,16 К. 
, где k является постоянной Больцмана (отношение универсальной газовой постоянной R к числу Авогадро NA), i — число степеней свободы молекул (i = 3 в большинстве задач про идеальные газы, где молекулы предполагаются сферами малого радиуса, физическим аналогом которых могут служить инертные газы), а T - абсолютная температура. Основное уравнение МКТ связывает макроскопические параметры (давление, объём, температура) газовой системы с микроскопическими (масса молекул, средняя скорость их движения).
34. Число степеней свободы механической системы. Число степеней свободы молекул. Закон равнораспределения энергии по степеням свободы молекулы. Число степеней свободы – это число независимых величин с помощью которых может быть задано положение системы. (1 атом =3 ст., 2 атома =5ст. 3 атома=6ст.) Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статической системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная КТ/2, а на каждую колебательную – КТ средняя энергия приходящаяся на одну степень свободы: 
У одноатомной молекулы i = 3, тогда для одноатомных молекул: 
для двухатомных молекул: 
Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходтся:
35. Работа, совершаемая газом при изменениях его объема. Графическое представление работы. Работа в изотермическом процессе. Для рассмотрения конкретных процессов найдем в общем виде внешнюю работу, совершаемую газом при изменении его объема. Рассмотрим, например, газ, находящийся под поршнем в цилиндрическом сосуде (рис. 78). Если газ, расширяясь, передвигает поршень на бесконечно малое расстояние d l, то производит над ним работу ΔA=Fdl=pSdl=pdV,
где S — площадь поршня, S dl=dV — изменение объема системы. Таким образом, ΔA=pdV. (52.1)Полную работу A, совершаемую газом при изменении его объема от V 1до V 2, найдем 
интегрированием формулы (52.1):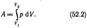 
Результат интегрирования определяется характером зависимости между давлением и объемом газа. Найденное для работы выражение (52.2) справедливо при любых изменениях объема твердых, жидких и газообразных тел. Изотермический процесс (T =const). Изотермический процесс описывается законом Бой ля — Мариотта: pV= const.
Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, расположенную на диаграмме тем выше, чем выше температура, при которой происходил процесс. Найдем работу изотермического расширения газа: 
Так как при T =const внутренняя энергия идеального газа не изменяется: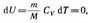 
то из первого начала термодинамики (Δ Q = dU+ΔA) следует, что для изотермического процесса
Δ Q= Δ A,т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: 
Следовательно, для того чтобы при работе расширения температура не уменьшалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.
36. Внутренняя энергия ТД системы как функция состояния. Теплота в процессе переноса энергии. Внутренняя энергия термодинамическая функция состояния системы, ее энергия, определяемая внутренним состоянием. Внутренняя энергия складывается в основном из кинетической энергии движения частиц (атомов, молекул, ионов, электронов) и энергии взаимодействия между ними (внутри- и межмолекулярной). На внутреннюю энергию влияет изменение внутреннего состояния системы под действием внешнего поля; во внутреннюю энергию входит, в частности, энергия, связанная с поляризацией диэлектрика во внешнем электрическом поле и намагничиванием парамагнетика во внешнем магнитном поле. Кинетическая энергия системы как целого и потенциальная энергия, обусловленная пространственным расположением системы, во внутреннюю энергию не включаются. В термодинамике определяется лишь изменение внутренней энергии в различных процессах. Поэтому внутреннюю энергию задают с точностью до некоторого постоянного слагаемого, зависящего от энергии, принятой за нуль отсчета. Внутренняя энергия U как функция состояния вводится первым началом термодинамики, согласно которому разность между теплотой Q, переданной системе, и работой W, совершаемой системой, зависит только от начального и конечного состояний системы и не зависит от пути перехода, т.е. представляет изменение фуникции состояния Δ U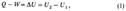 
где U1 и U2 - внутренняя энергия системы в начальном и конечном состояниях соответственно. Уравнение (1) выражает закон сохранения энергии в применении к термодинамическим процессам, т.е. процессам, в которых происходит передача теплоты. Для циклического процесса, возвращающего систему в начальное состояние, Δ U =0. В изохорных процессах, т.е. процессах при постоянном объеме, система не совершает работы за счет расширения, W =0 и теплота, переданная системе, равна приращению внутренней энергии: Qv =Δ U. Для адиабатических процессов, когда Q =0, Δ U =- W.
37.Первое начало ТД. Применение первого начала к различным изопроцессам. п ервый закон (первое начало) термодинамики можно сформулировать так: «Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщенного системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале μ, и работы A', совершённой над системой внешними силами и полями, за вычетом работы А, совершённой самой системой против внешних сил»: Δ U = Q − A + μΔ N + A '.Для элементарного количества теплоты δ Q, элементарной работы δ A и малого приращения (полного ифференциала) dU внутренней энергии первый закон термодинамики имеет вид: dU = δ Q − δ A + μ dN + δ A '. Разделение работы на две части, одна из которых описывает работу, совершённую над системой, а вторая – работу, совершённую самой системой, подчёркивает, что эти работы могут быть совершены силами разной природы вследствиеразных источников сил. Важно заметить, что dU и dN являются полными дифференциалами, а δ A и δ Q - нет. Приращение теплоты часто выражают через температуру и приращение энтропии: δ Q = TdS.
Изохорный процесс. (V=const).Диаграмма этого процесса (изохора) в координатах р, V изображается прямой, параллельной оси ординат (рис. 1), где процесс 1—2 есть изохорное нагревание, а 1—3 — изохорное охлаждение. При изохорном процессе газ не совершает работы над внешними телами, т. е 
Из первого начала термодинамики (δQ=dU+δA) для изохорного процесса следует, что вся теплота, которая сообщается газу, идет на увеличение его внутренней энергии: 
т.к. CV=dUm/dt, 
Тогда для произвольной массы газа получим 
(1) Изобарный процесс (p=const)Диаграмма этого процесса (изобара) в координатах р, V изображается прямой, которая параллельна оси V. При изобарном процессе работа газа при увеличения объема от V1 до V2 равна 
(2) и равна площади заштрихованного прямоугольника (рис. 2). Если использовать уравнение Менделеева-Клапейрона для выбранных нами двух состояний, то 
и 
откуда 
Тогда выражение (2) для работы изобарного расширения примет вид 
(3) Изотермический процесс (T=const). Изотермический процесс описывается законом Бойля—Мариотта: 
Диаграмма этого процесса (изотерма) в координатах р, V представляет собой гиперболу, которая расположена на диаграмме тем выше, чем выше температура, при которой происходит процесс. Исходя из формул для работы газа и уравнения Менделеева-Клайперона найдем работу изотермического расширения газа: 
Так как при Т=const внутренняя энергия идеального газа не изменяется:
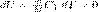то из первого начала термодинамики (δQ=dU+δA) следует, что для изотермического процесса 
т. е. все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил: 
(4)
38. Теплоемкость идеального газа. Уравнение Майера. Теплоемкость идеального газа — это отношение количества теплоты, сообщенного газу, к изменению температурыδТ, которое при этом произошло.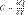 
Для любого идеального газа справедливо соотношение Майера: 
,где R — универсальная газовая постоянная,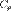 
— молярная теплоёмкость при постоянном давлении, 
— молярная теплоёмкость при постоянном объёме.Уравнение Майера вытекает из первого начала термодинамики, примененного к изобарическому процессу в идеальном газе: 
,в рассматриваемом случае: 
. 
Очевидно, уравнение Майера показывает, что различие теплоёмкостей газа равно работе, совершаемой одним молем идеального газа при изменении его температуры на 1 K, и разъясняет смысл универсальной газовой постоянной R — механический эквивалент теплоты.
39. Уравнение адиабаты идеального газа. Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением[ 
где: V — его объём, 
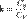— показатель адиабаты, 
и 
— теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.С учётом уравнения состояния идеального газа уравнение адиабаты может быть преобразовано к виду: 
,где T — абсолютная температура газа. Или к виду: 
Поскольку Kвсегда больше 1, из последнего уравнения следует, что при адиабатическом сжатии (то есть при уменьшении V) газ нагревается (T возрастает), а при расширении — охлаждается, что всегда верно и для реальных газов. Нагревание при сжатии больше для того газа, у которого больше коэффициент K.
40. Политропические процессы. Политропический процесс, политропный процесс, изменение состояния физической системы, при котором сохраняется постоянной её теплоёмкость (С). Кривая на термодинамических диаграммах, изображающая П. п., называется политропой. Простейшим примером обратимого П. п. может служить П. п. с идеальным газом, определяемый уравнением pVn = const, где р — давление, V — объем газа, 
показатель политропы (Cp и Cv — теплоёмкости газа соответственно при постоянном давлении и объёме). Используя уравнение состояния идеального газа, уравнение политропы можно записать в ином виде: 
const или 
const (здесь Т — абсолютная температура).уравнение П. п. идеального газа включает, как частные случаи, уравнения: адиабаты (С =0, n = Cp/Cv, это отношение теплоёмкостей обозначают g), изобары (С = Ср, n = 0), изохоры (С = Cv, n = ¥) и изотермы (С = ¥, n = 1). Работа А идеального газа в П. п. против внешнего давления определяется по формуле 
, где индексами 1 и 2 обозначены начальное и конечное состояния газа. Понятием П. п. широко пользуются в технической термодинамике при исследовании рабочих циклов тепловых двигателей.
41. Второе начало ТД. Тепловые двигатели и холодильники. Формулировка Клаузиуса.Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.Существуют несколько эквивалентных формулировок второго начала термодинамики: Постулат Клаузиуса: «Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему» [1] (такой процесс называется процессом Клаузиуса). Постулат Томсона (Кельвина): «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара» (такой процесс называется процессом Томсона).
Эквивалентность этих формулировок легко показать. В самом деле, допустим, что постулат Клаузиуса неверен, то есть существует процесс, единственным результатом которого была бы передача тепла от более холодного тела к более горячему. Тогда возьмем два тела с различной температурой (нагреватель и холодильник) и проведем несколько циклов тепловой машины, забрав тепло Q 1 у нагревателя, отдав Q 2 холодильнику и совершив при этом работу A = Q 1 − Q 2. После этого воспользуемся процессом Клаузиуса и вернем тепло Q 2 от холодильника нагревателю. В результате получается, что мы совершили работу только за счет отъёма теплоты от нагревателя, то есть постулат Томсона тоже неверен.С другой стороны, предположим, что неверен постулат Томсона. Тогда можно отнять часть тепла у более холодного тела и превратить в механическую работу. Эту работу можно превратить в тепло, например, с помощью трения, нагрев более горячее тело. Значит, из неверности постулата Томсона следует неверность постулата Клаузиуса.
Таким образом, постулаты Клаузиуса и Томсона эквивалентны. Теплово́йдви́гатель — устройство, совершающее работу за счет использования внутренней энергии топлива, тепловая машина, превращающая тепло в механическую энергию использует зависимость теплового расширения вещества от температуры. Действие теплового двигателя подчиняется законам термодинамики. Для работы необходимо создать разность давлений по обе стороны поршня двигателя или лопастей турбины. Для работы двигателя обязательно наличие топлива. Это возможно при нагревании рабочего тела (газа), который совершает работу за счёт изменения своей внутренней энергии. Повышение и понижение температуры осуществляется, соответственно, нагревателем и охладителем. Работа, совершаемая двигателем, равна: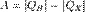 
, где: QH — количество теплоты, полученное от нагревателя, QX — количество теплоты, отданное охладителю. Коэффициент полезного действия (КПД) теплового двигателя рассчитывается как отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя: 
Часть теплоты при передаче неизбежно теряется, поэтому КПД двигателя менее 1. Максимально возможным КПД обладает двигатель Карно. КПД двигателя Карно зависит только от абсолютных температур нагревателя(TH) и холодильника(TX): 
Принцип действия теплового двигателя приведен на рис. 1. От термостата (система, которая может обмениваться теплотой с телами без изменения температуры) с более высокой температурой Т1, который называется нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, который называется холодильником, за цикл передается количество теплоты Q2, при этом совершается работа А = Q1 – Q2. Для того чтобы термический коэффициент полезного действия теплового двигателя был равен 1, нужно выполнение условия Q2 = 0, т. е. тепловой двигатель должен обладать одним источником теплоты, а это невозможно. Французский физик и инженер Н. Л. С. Карно (1796 — 1832) доказал, что для того, чтобы тепловой двигатель работал необходимо не менее двух источников теплоты с отличающимися температурами, иначе это противоречило бы второму началу термодинамики. Двигатель второго рода, будь он практически возможен, был бы практически вечным. К примеру, Охлаждение воды океанов на 1° дало бы практически неисчерпаемые запасы энергии. Масса воды в Мировом океане составляет порядка 1019 тонн, при охлаждении которой на 1° выделилось бы примерно 1024 Дж теплоты, что соответствует полному сжиганию 1014 т угля. Железнодорожный состав, который нагружен этим количеством угля, растянулся бы на расстояние 1010 км, что по порядку совпадает с размерами Солнечной системы! Процесс, который обратен происходящему в тепловом двигателе, используется в холодильной машине, принцип действия которой дан на рис. 2. Системой от термостата с более низкой температурой Т2 за цикл отнимается количество теплоты Q2 и отдается термостату с более высокой температурой Т1 количество теплоты Q1. Для кругового процесса, согласно первому началу термодинамики для кругового процесса, Q=A, но, по условию, Q = Q2 – Q1< 0, поэтому А<0 и Q2 – Q1 = –А, или Q1 = Q2 + A, т. е. количество теплоты Q1, которое отданно системой источнику теплоты при более высокой температуре T1 больше количества теплоты Q2, которое получено от источника теплоты при более низкой температуре T2, на величину работы, совершенной над системой. Значит, без совершения работы нельзя отбирать теплоту от менее нагретого тела и отдавать ее более нагретому. Это утверждение есть именно второе начало термодинамики в формулировке Клаузиуса. 
Используя второе начало термодинамики, Карно вывел теорему, которая носит теперь его имя: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T1) и холодильников (T2), наибольшим к. п. д. обладают обратимые машины; при этом к. п. д. обратимых машин, работающих при одинаковых температурах нагревателей (T1) и холодильников (T2), равны друг другу и не зависят от природы рабочего тела (тела, которые совершают круговой процесс и обмениваются энергией с другими телами), а определяются только температурами нагревателя и холодильника
42. Двигатель Карно. КПД двигателя Карно. Теорема Карно. Цикл Карно состоит из четырёх стадий: Изотермическое расширение (на рисунке — процесс A→Б). В начале процесса рабочее тело имеет температуру TH, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты QH. При этом объём рабочего тела увеличивается. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс Б→В). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника. Изотермическое сжатие (на рисунке — процесс В→Г). Рабочее тело, имеющее к тому времени температуру TX, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты QX. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс Г→А). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.При изотермических процессах температура остаётся постоянной, при адиабатических отсутствует теплообмен, а значит, сохраняется энтропия: 
Поэтому цикл Карно удобно представить в координатах T и S температураэнтропия КПД тепловой машины Карно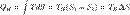 
Аналогично, при изотермическом сжатии рабочее тело отдало холодильнику 
Отсюда коэффициент полезного действия тепловой машины Карно равен 
Из последнего выражения видно, что КПД тепловой машины Карно зависит только от температур нагревателя и холодильника. Кроме того, из него следует, что КПД может составлять 100 % только в том случае, если температура холодильника равна абсолютному нулю. Это невозможно, но не из-за недостижимости абсолютного нуля (этот вопрос решается только третьим началом термодинамики, учитывать которое здесь нет необходимости), а из-за того, что такой цикл или нельзя замкнуть, или он вырождается в совокупность двух совпадающих адиабат и изотерм.Поэтому максимальный КПД любой тепловой машины, будет меньше или равен КПД тепловой машины Карно, работающей при тех же температурах нагревателя и холодильника. Например, КПД идеального цикла Стирлинга равен КПД цикла Карно. Первая теорема (более известна как формула Карно) Первая теорема Карно: DG + DH + DF = | DG | + | DH | − | DF | = R + r Пусть дан произвольный треугольник ABC. Тогда сумма алгебраических расстояний (англ.) от центра описанной окружности D до сторон треугольника ABC будет равна DF + DG + DH = R + r, где r — радиус вписанной окружности, а R — описанной. Знак расстояния принимается отрицательным тогда и только тогда, когда отрезок DX (X = F, G, H) целиком лежит вне треугольника. В ее доказательстве используется теорема Птолемея
Первая теорема Карно: DG + DH + DF = | DG | + | DH | − | DF | = R + r Вторая теорема (известная также как критерий Карно)
Пусть дан треугольник АВС и точки А1, В1, С1 на плоскости. Тогда перпендикуляры, опущенные из А1, В1, С1 на ВС, АС, ВС соответственно, пересекаются в одной точке тогда и только тогда, когда A 1 B 2 − A 1 C 2 + B 1 C 2 − B 1 A 2 + C 1 A 2 − C 1 B 2 = 0.
Следствие Перпендикуляры, опущенные из А1, В1, С1 на AB, АС, ВС соответственно, пересекаются в одной точке тогда и только тогда, когда перпендикуляры, опущенные из А, В, С на В1С1, А1С1, В1С1 соответственно, пересекаются в одной точке.
43. Энтропия. Из теоремы Клаузиуса следует, что приведенная теплота подобно энергии (потенциальной, внутренней) является функцией состояния (не зависит от пути перехода и зависит только от состояния системы). Независимость интеграла 
от пути перехода означает, что этот интеграл выражает собой изменение некоторой функции состояния системы, она называется энтропия и обозначается буквой S. Изменение энтропии системы, очевидно, равно 
|
Мы говорим только об изменении энтропии (подобно изменению потенциальной энергии, для которой не важно где начало отсчета). Из уравнения (9.30) вытекает основное количественное выражение второго начала термодинамики 
44. Энтропия и второе начало ТД.Выражая всеобщий закон сохранения и превращения энергии, первое начало термодинамики не позволяет определить направление протекания процесса. В самом деле, процесс самопроизвольной передачи энергии в форме теплоты от холодного тела к горячему ни в какой мере не противоречит первому закону термодинамики. Однако при опускании раскаленного куска железа в холодную воду никогда не наблюдается явление дальнейшего нагревания железа за счет соответствующего охлаждения воды. Далее, первое начало не исключает возможности такого процесса, единственным результатом которого было бы превращение теплоты, полученной от нагревателя в эквивалентную ей работу. Так, например основываясь на первом начале можно было бы попытаться построить периодически действующий двигатель, совершающий работу за счет одного источника тепла (например за счет внутренней энергии океана). Такой двигатель называется вечным двигателем второго рода. Обобщение огромного экспериментального материала привело к выводу о невозможности построения вечного двигателя второго рода. Этот вывод получил название второго начала термодинамики.Существует ряд различных по форме, одинаковых по существу формулировок второго начала:Невозможен процесс, единственным результатом которого является превращение всей теплоты, полученной от нагревателя, в эквивалентную ей работу. Формулировка Клаузиуса: теплота сама собой не может переходить от менее нагретого тела к более нагретому. Формулировка Томсона-Планка: перпетууммобиле второго рода невозможен.Из теоремы Клаузиуса следует, что приведенная теплота подобно энергии (потенциальной, внутренней) является функцией состояния (не зависит от пути перехода и зависит только от состояния системы). Независимость интеграла.  от пути перехода означает, что этот интеграл выражает собой изменение некоторой функции состояния системы, она называется энтропия и обозначается буквой S. Изменение энтропии системы, очевидно, равно 
|
Мы говорим только об изменении энтропии (подобно изменению потенциальной энергии, для которой не важно где начало отсчета). Из уравнения (9.30) вытекает основное количественное выражение второго начала термодинамики 
