В зубчатых мех. усилие от одного звена к другому передается при помощи взаимодействующих поверхностей звеньев высших пар, которые обеспечивают заданный закон их относит ельного движ. и назваются сопряженными поверхностями
Для воспроизведения непрерывного движения в дном направлении необходимо иметь несколько последующих пар сопряженных плоскостей, В зубчатых мех.сопряженные пов. располагаются на выступах, которые называются зубьями.
Высшая КП,образуемая последовательными взаимодействующими сопряженными поверхностями зубьев называются зубчатым зацеплением
Хар-р относительного движения 2-х тел образующих высшую пару зубчатого зацепления находиться в тесной связи с геометрией сопряж. поверхностей. Изучение геометрии сопряж. поверхн. составляет элемент теории зацепления.
|
передача называется эвольвентной. Эвольвентное зацепление бы предложено Л. Эйлером Ч
Теорема зацепления
Основная теорема зацепления
общая Нормаль, к сопряженным профилям проведенная через точку их касания делит линию межосевого расстояния на части обратно пропорциональные угловым скоростям.
Теорема утверждает, что 
;
Построим заменяющий механизм, для этого найдем радиусы кривизны. Считаем звено АВ жестким.
подобны (прямоугольные), тогда
Свяжем со звеньями 1 и 2 плоскости I и II. Геометрические места точек П в системе звеньев 1 и 2 образуют центроиды Ц1 и Ц2, которые перекатываются друг по другу без скольжения.
Одно и тоже движение звеньев можно получить при помощи криволинейных профилей 1 и 2 и центроид Ц1 и Ц2.
Точка П называется полюсом зацепления.
Зацепление называется внешним если центроиды касаются внешним образом, а нормаль n-n делит линию межосевого расстояния внутренним образом.
– внутреннее зацепление
При постоянном передаточном отношении пояс зацепления неподвижен, а центроидами являются окружности.
Если на одном колесе зададим профиль 2, то другой профиль 1 получится как огибающая кривая ряда последующих положений профиля 2.
Сопряженные профили перекатываются друг по другу со скольжением
Чем дальше точка контакта находится от полюса зацепления тем больше потери на трение, поэтому сопряженные профили располагают вблизи центроид.
При контакте зубьев в полюсе скорость скольжения равна 0.
2.3 Эвольвента окружности: ее образование, уравнения и свойства.
В 1750-1762 годах Леонардо Эйлером было предложено профили зубьев вычерчивать по эвольвенте окружности.
Эвольвента получается путем перекатывания прямой линии по окружности без скольжения, тогда каждая прямая опишет эвольвенту.
Радиус основной окружности rв.
; 
; 
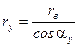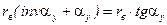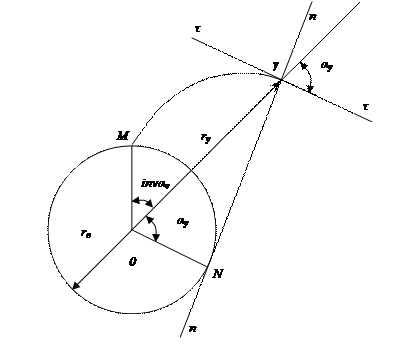
invαy – полярный угол – инволюта αy.
Свойства эвольвенты:
1) Нормаль к эвольвенте проходит касательно к основной окружности.
2) Расстояние NY является радиусом кривизны эвольвенты NY=ρy
3) По мере удаления точки эвольвенты от основной окружности, радиус кривизны увеличивается.
Если rb→∞, то ρy→∞, т.е. эвольвента тоже вырождается в прямую линию.
3.6 Геометрия сопряженных эвольвентных профилей при внешнем зацеплении.
Прямая N1N2 принадлежит неподвижной плоскости и является геометрическим местом точек касания сопряженных эвольвентных профилей и называется линией зацепления.
Угол αω, образованный между линией зацепления и перпендикуляром к межосевому расстоянию, проходящим через полюс зацепления П, называется углом зацепления.
Выполняется теорема о перекате профилей со скольжением.
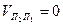, в остальных точках ≠0.
Свойства эвольвентного зацепления:
1) Постоянное передаточное отношение.
2) Независимость передаточного отношения от изменения величины межосевого расстояния. (При изготовлении межосевого расстояния будет допуск).
При увеличении межосевого расстояния линия зацепления снова пройдет касательно к основным окружностям и будет пересекать линию межосевого расстояния в другой точке П, появятся новые начальные окружности с диаметрами dω1` и dω2` и будет и другой угол зацепления (но все это в небольших пределах).
Зависимость угла поворота второго колеса от первого.
Для передач кривая зависит от изменения межосевого расстояния.
3) Усилия между зубьями направлены по линии зацепления (R12 и R21), которая в процессе работы не изменяет своего направления, проходит касательно к основным окружностям, это благоприятно влияет на действие механизма.
4) Просто осуществить взаимозаменяемость.
5) Просто изготовить на современном оборудовании.
Недостатки:
1) Высокие контактные давления в высшей паре.(относительно малые радиусы кривизны что снижает площадь в передаче)
- (формула Герца-Беляева).
“+” – при внешнем зацеплении.
2) Значительные потери на трение.
Геометрия сопряженных эвольвентных профилей при внутреннем зацеплении.
Прямая N1N2 – мнимая линия зацепления, т.к. на ней профили зубьев касаться не могут. Реальный контакт зубьев осуществляется на прямой N1n.
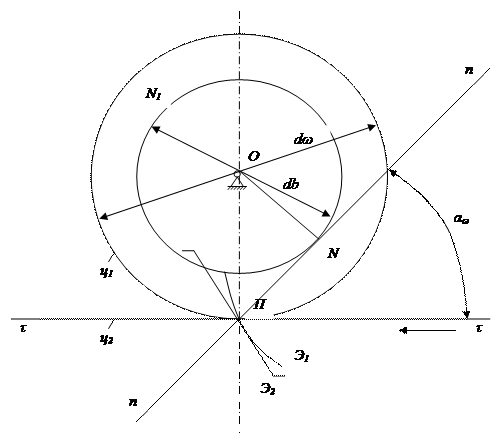
При внутреннем зацеплении скорость скольжения будет меньше, поэтому будут меньше потери на трение.
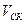- скорость скольжения.
габариты будут меньше.
Реечное зацепление.
Реечное зацепление применяют для преобразования вращательного движения в поступательное и наоборот.
Профиль зуба рейки вырождается в прямую линию, перпендикулярную к образующей прямой Nn.
Т.к рейка совершает поступательное движение, то для того чтобы прямая n-n была в виде зацепления и нормаль сопр. профиля всегда проходила через полюс р необходимо чтобы все нормали были // n-n. В этом случае профиль зуба рейки должен быть прямой линией ┴ к n-n С точки зрения контю прочности и потерь на трение реечное зацепление занимает промежуточное положение между внешним и внутренним зацеплением.
3.7 Зубчатое колесо и его элементы.
Зубья расположены в соответствии с угловым шагом τ.
Угловому шагу соответствует окружной шаг Py (это шаг по окружности диаметром dy).
Окружной шаг – расстояние, измеренное по дуге окружности между одноименными профилями соседних зубьев.
Угловая толщина зуба 2ψy.
Угловая ширина впадины 2ηy
Ширина зуба Sy
Ширина впадины ey
Диаметр окружности впадины df
Диаметр окружности вершины da
Для обеспечения непрерывности передачи вращательного движения в некоторые моменты времени в контакте должно находиться две пары зубьев одновременно.
Pα – шаг зацепления.
ab = a`b`
db – диаметр основной окружности.
Делительной окружностью называется окружность стандартных шага р, модуля m и угла профиля a.
Шаг – расстояние между одноименными точками двух соседних профилей зубьев, измеренные по дуге соответствующей окружности.
Модулем называется часть диаметра делительной окружности, приходящаяся на один зуб.
Модуль m,[мм] – стандартная величина и определяется по справочникам, исходя из трех рядов:
1 ряд – наиболее предпочтительный;
2 ряд – средней предпочтительности;
3 ряд – наименее предпочтительный.
Модуль характеризует высоту зуба. Чем больше зуб, тем более шумной становится зубчатая передача.
Угол профиля – угол между касательной к эвольвенте в данной точке и радиус-вектором данной точки (см. чертеж эвольвенты).
Угол профиля для точки, лежащей на делительной окружности, является величиной стандартной и равной 20о (хотя лучше 25о).
3.8 Условием правильного сопряжения эвольвентных колес является равенство их основных шагов.
Pb = Pα
Если Pb1 = Pb2 = Pα – зацепление возможно …..
3.9 Исходный контур.
Во всех странах для стандартизации зубчатых колес приняты параметры зубчатой рейки с прямолинейным профилем.
Параметры зубчатой рейки, положенные в основу стандарта для определения элементов и размеров семейства зубчатых колес, представителями которого рейка и является, называется исходным контуром.
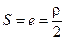
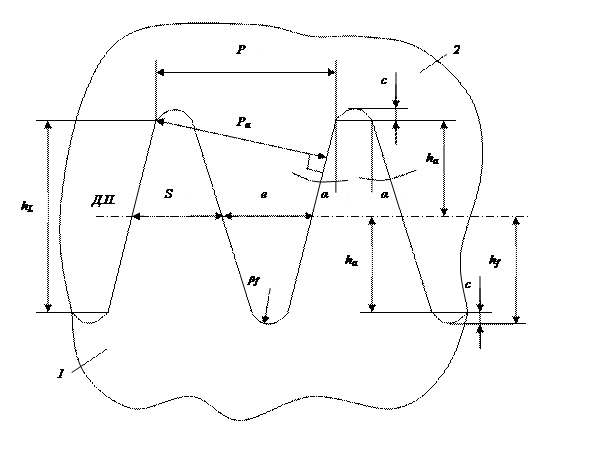
Pα – шаг зацепления.
Д.П. – делительная прямая, имеющая одинаковые S.
ha - делительная высота головки зуба.
hf – делительная высота ножки зуба.
с – радиальный зазор.
hL – граничная высота зуба.
α – угол профиля.
ρf – радиус зацепления.
При зацеплении колеса с рейкой центроидами являются у колеса – окружность, а у рейки – любая прямая, параллельная Д.П.
Окружность колеса перемещается по прямой рейки без скольжения.
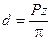
Модуль зацепления будет равен:
Окружность с диаметром d принимают за базу для определения элементов и размеров зубьев.
Значение модуля (m) стандартизовано от 0,05 до 100 мм.
Окружность, для которой m имеет стандартизованное значение, называется делительной.
Шаг по делительной окружности равен шагу рейки P.
Диаметр d строго постоянный, не зависит от качества изготовления.
, где 
(чаще всего).
, где 
, где 
чаще всего 
, где 
В автомобильной промышленности:
3.10 Способы изготовления зубчатых колес
Существуют два основных способа изготовления зубчатых колес:
1. копирование: профиль зуба инструмента (протяжка) переносится, и он оставляет след. Способ очень неточный, малопроизводительный и требует наличие инструмента в большом ассортименте, различаемых по модулю и количеству зубьев. Применяется в мелко серийном производстве.
основным недостатком способа явл. то, что для каждого сочетания модуля и числа зубьев нужно иметь инструмент
стандарты модулей:число зубьев превышает 100
для сокращения номенклатурного инструмента диапазон числа зубьев разбивают на интервалы и в пределах каждого интервала прим. одну и ту же фрезу при нарезании
колёс с разным числом зубьев.(прим. комплекты из 8 15 и 26 фрез)
положит явл. то что не требуется спец оборудования и погрешности связанные с несоответствием числа зубьев колеса в этом случае отсутствуют
2 обкатка (см. лаб.раб. №8): инструменту и заготовке сообщают такое относительное движение, при котором огибающая к положению режущей кромке инструмента очерчивает эвольвенту. Инструмент может быть различным: рейки (гребенки), долбяки и фрезы.
профиль зуба формируется как огибающая кривая в положении профиля зуба инструмента и его отн. движении относительно заготовки.
нарезание зубьев червячной фрезой
ч ерв. фреза представляет собой винт с трапецеидальной резьбой профиль которой в нормальном сечении совпадает с профилем рейки.
3.13 Определение геометрических параметров эвольвентного зацепления зубчатой пары
Известные параметры исх контура: 
и коэффициенты смещения исходного контура, угол беззазорного зацепления. Беззазорным называют зацепление, в котором отсутствует боковой зазор под которым понимают расстояние по контактной нормали между нерабочими профилями зубьев
В силовых передачах боковой зазор служит для компенсации температ. расширений зубьев В точных расчетах передач боковой зазор – вредное явление
при беззазорном зацеплении толщина зуба по дуге начальной окружности одного колеса должна быть равна ширине впадин др.колеса т.к. эти окружности перекатываются друг по другу без скольжения 
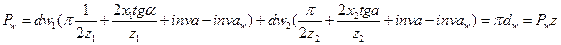
МЕЖОСЕВОЕ РАССТОЯНИЕ
3.14 Зубчатые передачи со смещением и без смещения (рис. 11-86).
Эвольвентную зубчатую передачу составляют, как минимум, из 2-х зубчатых колес, при этом в рассмотрение вводится две начальные окружности радиусами rw1 и rw2.
Меньшее зубчатое колесо в обычной понижающей зубчатой передаче называется шестерня.
Вместо производящей прямой здесь вводится в рассмотрение линия зацепления N1N2, которая одновременно касается 2-х основных окружностей rb1 и rb2.
Линия зацепления является геометрическим местом точек контакта сопряженных эвольвентных профилей. В точке В1 пара эвольвент, которые в данный момент времени контактируют в точке К, входят в зацепление. В точке В2 этаже пара эвольвент из зацепления выходят.
На линии зацепления N1N2 все взаимодействующие эвольвенты при зацеплении касаются друг друга. Вне участка N1N2 эвольвенты пересекаются, и если такое случится, то произойдет заклинивание зубчатого колеса.
Угол 
N1O1P = N2J2P = aw – угол зацепления.
Для передачи, составленной из нулевых зубчатых колес aw=20o
Для передачи, составленной из положительных з. к. aw>20o
Для передачи, составленной из отрицательных з. к. aw<20o
c=c*.m - радиальный зазор, величина стандартная, необходим для нормального обеспечения смазки.
c* - коэффициент радиального зазора, по ГОСТ c*=0.25 (c*=0.35).
Между делительными окружностями у.m – это воспринимаемое смещение.
у – коэффициент воспринимаемого смещения, он имеет знак, и в зависимости от знака различают:
1. у=0 у.m=0 – нулевая зубчатая передача;
2. у>0 у.m>0 – положительная зубчатая передача;
3. у<0 у.m<0 – отрицательная зубчатая передача;
Свойства эвольвентного зацепления.
1. Эвольвентное зацепление молочувствительно к погрешностям изготовления, т.е. при отклонении межосевого расстояния от номинала передаточное отношение зубчатой передачи не изменится.
2. Линия зацепления N1N2 является общей нормалью к сопряженным эвольвентным профилям.
3. Контакт эвольвент осуществляется только на линии зацепления.
3.37 Планетарные механизмы.(п.м.)
П.м. содержат зубчатые колеса с подвижными геометрическими осями. Эти колеса называются сателлитами.
Механизм Джемса:
|
Сателлитов может быть и больше.
Звено Н, на котором расположены оси вращения сателлитов, называются водилом.
Зубчатые колеса, геометрические оси которых совпадают с осью вращения водила, называются центральными.
1- подвижное центральное колесо (солнечное).
2- неподвижное центральное колесо (коронное).
В этом механизме главная характеристика:
- перед. отношение от 1 ого колеса к водила, при неподвижном 3-ем.
П.о. планетарных механизмов определяют по методу обращения движения, для этого всем звеньям сообщают вращение со скоростью: 
, тогда водило, будет неподвижным, а остальные звенья получат дополнительное вращение со скоростью .
Механизмы, получающиеся при остановленном водила называются обращенными.
В этом механизме оси всех колес неподвижны.
| Звено | Основной механизм | Обращенный механизм |
| ω1 | ω1- ωн | |
| ω2 | ω2- ωн | |
| 0 | -ωн | |
| ωн | 0 |
При неподвижном водиле:
П.о. планетарного механизма от какого либо колеса к водила равно: единица минус передаточное отношение от того же колеса(1ого) к неподвижному колесу при остановленном водиле.
Это справедливо к любому колесу.
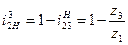
От водила к первому колесу:
От первого колеса ко второму:
Механизмы типа Джемса применяют для получения п.о.-ий по сравнению с механизмами с неподвижными осями при меньших габаритах и массе по сравнению с механизмами с неподвижными осями т.к в них используется несколько сателлитов, что уменьшает усилие на каждую пару зубьев, что позволяет применять колеса с меньшими модулями. Но эти механизмы требуют высокой точности изготовления.
Планетарные механизмы с 2мя внешними и 2мя внутренними зацеплениями.
(Механизмы Давида)
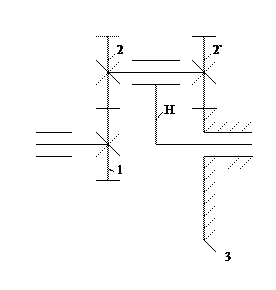
С внешним зацеплением. С внутренним зацеплением.
; «+» - с внешним зацепление, «-» - с внутренним зацеплением.
z1=100
z2=99
z3=101
z4=100
Механизмы Давида применяют для получения очень больших передаточных отношений в несиловых передачах и в силовых передачах кратковременного действия (практически до 1700)
3.40 Кинематика зубчатых дифференциалов.
Дифференциальными механизмами называют планетарные механизмы, обладающие 2мя и более степенями свободы.
- подвижных колес.
1) Остановим 1 колесо:
; 
; 
;
2) Остановим 3 колесо:
; 
; 
;
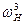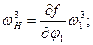
Угловая скорость ведомого вала дифференциала с 2мя степенями свободы равна сумме 2х слагаемых, каждое из которых равно произведению угловой скорости данного ведущего вала на передаточное отношение от ведомого вала к данному ведущему валу при остановленном другом ведущем вале.
Определим передаточные отношения:
Окончательно угловая скорость будет равна:
Дифференциальные механизмы применяют:
1- для привода одного рабочего органа от двух двигателей или для сложения движения 2х ведущих звеньев на ведомом валу.
2- для привода 2х рабочих органов с независимыми скоростями от одного двигателя или для разложения движения ведущего вала на 2 независимые движения ведомых валов.
3.38 Кинематика волновой передачи.
Волновая передача является частным случаем планетарной передачи (молодая передача- 50 лет)
|
Передача двухволновая.
1-жеское колесо
2-гибкое
3-генератор волн (водила)
4-ролик.
До 50% зубьев находится в зацеплении.
Эта передача позволяет получать большие передаточные отношения. Ее целесообразно применять при передаточном отношении более 80.
“+”- имеет малые габариты, высокие КПД.
“-” - зубчики снаружи - концентратор напряжения.
3.40 Кинематика зубчатых дифференциалов.
Дифференциальными механизмами называют планетарные механизмы, обладающие 2мя и более степенями свободы.
- подвижных колес.
1) Остановим 1 колесо:
; ; ;
2) Остановим 3 колесо:
; ; ;
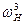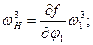
Угловая скорость ведомого вала дифференциала с 2мя степенями свободы равна сумме 2х слагаемых, каждое из которых равно произведению угловой скорости данного ведущего вала на передаточное отношение от ведомого вала к данному ведущему валу при остановленном другом ведущем вале.
Определим передаточные отношения:
Окончательно угловая скорость будет равна:
Дифференциальные механизмы применяют:
3- для привода одного рабочего органа от двух двигателей или для сложения движения 2х ведущих звеньев на ведомом валу.
4- для привода 2х рабочих органов с независимыми скоростями от одного двигателя или для разложения движения ведущего вала на 2 независимые движения ведомых валов.
Конические дифференциалы.
- ведущие звенья (углы поворота 1 и 3 колес).
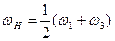
Автомобильный дифференциал.
Исследование кинематики планетарных и дифференциальных механизмов графическим методом.
Заданы 
и 
.
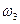Определим скорости в т. а и в т. b:
Масштабный коэффициент:
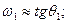
p – полюс плана угловых скоростей.
Определим масштабный коэффициент:
4.7 Силы трения в кинематических парах. Понятие о приведённом коэффициенте трения.
(Силы вредного сопротивления)
1- Случай плоского ползуна:
2- Случай клинчатого ползуна.
; 
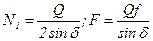
Приведенный коэффициент трения f` равен отношению суммарной силы трения к суммарной силе N (нормальной реакции опоры).
При этом силы нормального давления суммируются геометрически, а силы трения алгебраически.
Тогда 
Направляющий металлорежущего станка:
Тогда: 
Цилиндр, ползун: 
3- Трение во вращающей паре. (случай цапфы с относительно большим зазором).
ρ – угол трения.
r – радиус цапфы.
М – момент трения.
- цапфа с небольшим зазором.
Случай цапфы без зазора.
Новая цапфа.
В этом случае
Приработавшаяся цапфа.
Для шариковых и роликовых подшипников значения приведенных коэффициентов трения приводятся в справочнике «подшипники качения».
4.8 Определение сил инерции звеньев.
JS – момент инерции звена, проходящего через центр масс.
Исследование движения механизмов под действием заданных сил.
Для исследования движения механизмов можно использовать теорему об изменении кинетической энергии:
А – работа.
Т – кинетическая энергия.
Работа внешних сил идет на изменение кинетической энергии.
Данное выражение представляется довольно громоздким даже для механизмов с небольшим числом звеньев вследствие необходимости суммирования по n-звеньям. Для механизма с одной степенью свободы можно получить более простую запись этого уравнения, при которой все операции суммирования по n-звеньям выписываются заранее.
С этой целью уравнение движения можно заменить тождественным ему уравнением движения одного звена (или одной точки звена), которое движется так, что его координата в любой момент времени совпадает с обобщенной координатой механизма.
4.9 Приведение сил и моментов. Приведение масс и моментов инерции звеньев.
На рис. 1 ведущее звено совершает вращающее движение.
Уравнение движения заменим уравнением движения одного вращающегося звена ОА, которое называется звеном приведения.
К звену приведения приложена пара сил с моментом Мп, которые заменяют все силы и моменты, действующие на звенья механизмов.
Момент Мп называется приведенным моментом сил, под которым понимают условный момент, приложенный к звену приведения, элементарная работа которого на возможном перемещении = сумме элементных работ заменяемых сил и механизмов. При стационарных связях равенство элементных работ одновременно означает равенство мощностей.
- мощность приведенного момента.
- мощность элементарной силы.
- мощность элементарного момента.
Приведенный момент равен:
Если звено приведения совершает поступательное движения (рис.2), то к нему прикладывают силу Рп, которая заменяет все силы и моменты, действующие на звенья механизма и называются приведенной силой, под которой понимают условную силу, приложенную к звену приведения, точке приведения А, элементная работа которой на возможное перемещение = сумме элементных работ заменяемых сил и моментов.
Решая относительно приведенной силы:
- приведенная сила.
Если для каждого положения механизма известны приложенные к его звеньям силы и моменты, то приведенная сила и приведенный момент будут зависеть только от отношения скоростей, которые зависят от положения механизма, следовательно, определения приводимых сил и моментов можно выполнить до решения уравнения движения.
Приведение масс и моментов инерции звеньев.
При вращательном движении звено ОА обладает моментом инерции Jр, относительно оси его вращения, который заменяет все массы и моменты инерции звеньев и называется приведенным моментом инерции - условный момент инерции, которым должно обладать звено приведения относительно оси его вращения, чтобы кинетическая энергия этого звена в каждом рассмотренном движении механизма была бы равна сумме кинетических энергий всех его звеньев.
Решив это уравнение относительно Jп, получим
Если звено приведения совершает поступательное движение, то все массы, моменты заменяют одной массой, сосредоточенной в одной точке приведения т. А - приведенная масса – условная масса, сосредоточенная в точке приведения, а ее кинетическая энергия равна сумме кинетических энергий всех звеньев механизма в каждом рассматриваемом положении.
Решая относительно приведенной массы mп:
Приведенная масса и приводимый момент инерции всегда положительный и зависит только от отношения скоростей, т.е. от положения механизмов. Определения приведенных масс и приведенных моментов инерции можно выполнить до решения уравнения движения механизма.
4.10 Дифференциальные уравнения движения механизмов
Это уравнение можно получить из уравнения об изменении кинетической энергии в дифференциальной форме и из уравнения Лагранжа II рода.
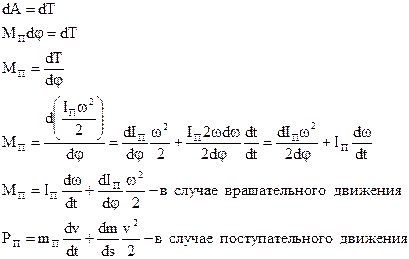
Приведение сил и моментов, масс и моментов инерции значительно упрощает запись уравнения движения, т.к. в этом случае имеем дело с расчетной схемой, состоящей из одного звена приведения нагруженного приведенным моментом сил (силой) и обладающего приведенным моментом инерции (массой). Эта расчетная схема получила название одномассовой динамической моделей механизма.
4.11 Интегрирование уравнения движения механизма в дифференциальной форме
- момент движущих сил; 
- момент сил сопротивления; 
(грузоподъемные машины, токарные станки)
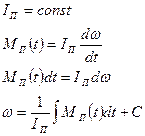
Численное интегрирование уравнения движения механизма в дифференциальной форме по методу Баранова
тогда уравнение примет вид
Решаем это уравнение относительно 
Но этот способ не достаточно точный.
4.12 Режимы движения. Разбег, установившееся движение, выбег. Средняя скорость, коэффициент неравномерности движения.
Интегрированием уравнения движения механизма можно получить зависимость скорости звена приведения от времени.
ТР – стадия (время, период) разбега, когда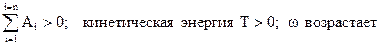 
.
ТУД – время установившегося движения
Установившимся движением называется движение, при котором скорость звена приведения является периодической функцией времени, а период изменения этой скорости называется циклом установившегося движения.
Та = Тb, а внутри цикла работа всех внешних сил отлична от нуля, следовательно, звено приведения будет двигаться неравномерно.
Важной кинематической характеристикой является коэффициент неравномерности движения
Действительной средней угловой скоростью называют скорость такого равномерного движения, при котором ведущее звено повернется на угол φ за тот же промежуток времени t, который требуется и при неравномерном движении.
ТВ – время выбега; 
Режимы разбега и выбега, а также режимы перехода от установившегося движения с одной скоростью к установившемуся движению с другой скоростью называют переходными.
Переходные режимы в динамическом отношении более нагружены (опасны)
Как обеспечить постоянство скорости?
Запишем уравнение движения:
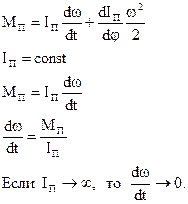
Практически регулирование скорости при установившемся движении осуществляется за счет увеличения приведенного момента инерции, чаще всего на одном из звеньев устанавливают маховик.
Для определения момента инерции маховика необходимо знать при силах зависящих от положения механизма, следующее:
1) приведенный момент движущих сил и сил сопротивления за один полный цикл установившегося движения;
2) приведенный момент инерции звеньев механизма за полный цикл в функции угла поворота ведущего звена;
3) средняя угловая скорость;
4) коэффициент неравномерности движения.
Момент инерции будем определять по методу Мерцалова Н.И.
1) Строим график приведенного момента сил сопротивления.
Отрицательные значения МПС строятся как положительные.
2) 
Интегрируя график приведенного момента сил сопротивления, получаем зависимость работы приведенного момента сил сопротивления от угла поворота.
3) Предполагаем, что движущий момент постоянный и учитывая, что вначале и в конце цикла установившегося движения имеет равенство работ сил движущих и сил сопротивления, строим график работы движущих сил.
4) Строим график изменения кинетической энергии.
Перепад этих энергий будет равен
Динамический эффект маховика
Энергетический баланс маховика
Маховик является аккумулятором механической энергии при холостом ходе он ее накапливает а при рабочем отдает.
Где выгодно установить маховик (на каком звене)?
Два вала: 
Выгодно маховик установить на быстро вращающемся звене, но при этом следует учитывать жесткость кинематической цепи, соединяющей двигатель с маховиком.
Иногда можно осуществить регулирование скорости за счет подбора механических характеристик двигателя и машины.
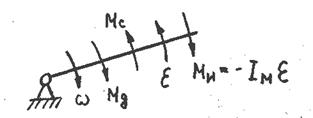
4.13 Силовой анализ механизмов
Целью силового анализа является определение реакций кинематических пар, которые необходимы для расчета звеньев механизма на прочность. Различают два случая силового расчета. В первом случае задача ставится так: известны размеры, массы и моменты инерции звеньев, известен закон движения ведущего звена; силы, действующие на звенья механизма. Требуется определить реакции кинематической пары и уравновешивающую силу или уравновешивающий момент, приложенные к ведущему звену. Силы инерции звеньев в данном случае определяется в соответствии с заданным законом движения ведущего звена.
Во втором случае задача ставится так: известны размеры, массы и моменты инерции звеньев, все силы, действующие на звенья механизма. Требуется определить реакции в кинематической паре. В этом случае закон движения ведущего звена определяется после решения уравнения движения и в соответствии с этим законом движения ведущего звена определяются силы инерции звеньев. Первый случай является предварительным, а второй окончательным.
Силовой расчет осуществляется погруппно, т.е. рассматривают каждую структурную группу отдельно. Начиная со структурных групп, наиболее удаленных по кинематической цепи от главного звена. А далее в порядке обратном порядку присоединения структурных группы при образовании механизма.
4.14 Определение реакции в кинематических парах. Силовой расчёт механизмов с низшими парами.
Статическая определимость кинематической цепи
Известно: точка приложения;
Неизвестно: направление, величина.
Известно: направление;
Неизвестно: точка приложения, величина.
Таким образом, каждая пара пятого класса дает две неизвестных. Каждое звено в плоской системе сил дает три уравнения.
3n уравнений, n – число звеньев
2p5
3n = 2p5
3n - 2p5 = 0 – уравнение структурных групп Ассура.
Статически определимыми кинематическими цепями являются группы Ассура (или структурные группы)
При силовом расчете структурных групп пользуются принципом Даламбера (принцип кинетостатики)
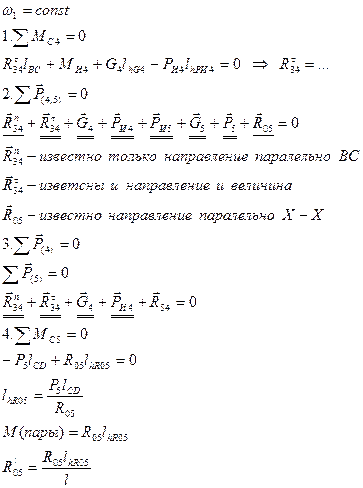
1. 
2. Рассмотрим равновесие всей группы
3. 
Силовой расчет ведущего звена
Случай уравновешивания ведущего звена уравновешивающей силой
1. 
2. 
Случай уравновешивания ведущего звена уравновешивающим моментом
4.15
|
|
4.16
5.1 Силы трения в кинематических парах. Понятие о приведённом коэффициенте трения.
(Силы вредного сопротивления)
4- Случай плоского ползуна:
5- Случай клинчатого ползуна.
;
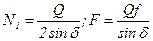
Приведенный коэффициент трения f` равен отношению суммарной силы трения к суммарной силе N (нормальной реакции опоры).
При этом силы нормального давления суммируются геометрически, а силы трения алгебраически.
Тогда
Направляющий металлорежущего станка:
