Обработка результатов измерения на ЭВМ

Эксперимент.

Блок-схема установки изображена на рис. 5. Она состоит из:
1 – свинцового контейнера, внутрь которого помещается радиоактивный источник; 2 – сцинтилляционного детектора; 3 – низковольтного и
4 – высоковольтного источников питания детекторов; 5 – детекторного блока с тумблером переключения детекторов (в положении «8» - сцинтилляционный детектор, а в положении «9» – счетчик Гейгера-Мюллера); 6 – свинцовый домик со счетчиком Гейгера-Мюллера; 7 – пересчетного устройства ПП-9 и
8 – цифропечатающего устройства Б3-15.

Цель эксперимента состоит в получении двух массивов экспериментальных значений числа набранных импульсов в последовательном ряде 3-х секундных интервалов времени: 200 измерений от естественного радиоактивного фона и 500 измерений от исследуемого радиоактивного источника.

ИЗМЕРЕНИЕ

1. Включите тумблер «сеть» пересчетного прибора, цифропечатающего устройства, а также низковольтного и высоковольтного источников питания.

2. После прогрева высоковольтного источника в течение 3 минут включите на нем переключатель «Высокое напряжение».

3. На пересчетном приборе нажмите кнопку «Стоп».

4. На детекторном блоке установки установите тумблер в положение, обозначенное цифрой «8».

5. На пересчетном приборе установите время экспозиции на 3 секунды.

6. Нажмите кнопки «Сброс» на пересчетном приборе и на цифропечатающем устройстве.

7. На пересчетном приборе нажмите кнопку «Пуск ЦПУ»

8. После того как цифропечатающее устройство зарегистрирует 200 измерений от естественного фона, нажмите кнопку «Стоп» на пересчетном приборе.

9. Удалите из цифропечатающего устройства распечатку с измерениями.

10. Поместите в свинцовый домик радиоактивный источник.

11. Нажмите кнопки «Сброс» на пересчетном приборе и на цифропечатающем устройстве.

12. На пересчетном приборе нажмите кнопку «Пуск ЦПУ»

13. После того как цифропечатающее устройство зарегистрирует 500 измерений от источника и естественного фона, нажмите кнопку «Стоп» на пересчетном приборе.

14. Удалите из цифропечатающего устройства распечатку с измерениями и выключите установку.

15. Вручную произведите сортировку экспериментальных данных. Для этого отдельно для 200 и 500 измерений составьте таблицу из двух колонок. В первую колонку в возрастающем порядке занесите число импульсов, зарегистрированных в отдельном измерении, а, напротив, во вторую колонку частоту их повторения.

ЗАДНИЕ

1. Обработать экспериментальные данные на ЭВМ (см. приложение I).

2. Используя расчетные данные оценить средние значения и указать точность оценки при доверительной вероятности 0.7 и 0.95.

3. Проверить, пользуясь критериями согласия Пирсона и Колмогорова-Смирнова согласие полученных наблюдений с предположением, что статистика числа зарегистрированных импульсов подчиняется законам Пуассона и Гаусса (см. приложения II и III) при уровне значимости 0.05.

4. Проанализировать, пользуясь качественным методом, согласие полученных наблюдений с предположением, что статистика числа зарегистрированных импульсов подчиняется законам Пуассона и Гаусса.

5. Для отчета по работе представляются 2 распечатки расчетов на ЭВМ, ленты АЦПУ.

В0ПРОСЫ

1. Знать определение среднего значения, дисперсии, стандартного отклонения среднеквадратичной ошибки.

2. Распределение Пуассона и Гаусса. Связь между этими распределениями.

3. Уметь найти аналитический вид формул для расчета ошибок следующих функций:

; ; ; ; ,

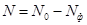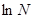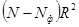где t и R считать точными значениями.

Приложение I

Обработка результатов измерения на ЭВМ.

Изучите теоретический материал к лабораторной работе «Изучение статистики радиоактивного распада [1,2].

Большая часть предварительных расчетов в этой работе производится на ЭВМ с помощью программы Stat2.xls. Для этого нужно открыть этот файл из стандартного приложения Microsoft Excel. В окне предупреждения нажмите кнопку «Не отключать макросы».

После открытия файла на экране появится таблица, похожая на ту, которую Вы получили для 200 измерений естественного фона. С помощью клавиатуры замените исходные значения в колонках A и B значениями, полученными в эксперименте.

Из основного меню выберите СервисÞМакросÞМакросы…. В появившемся окне выберите имя макроса «Статистика» и нажмите кнопку «Выполнить». По истечении некоторого времени программа выведет на экран необходимые для дальнейшей работы результаты расчета.

С помощью полос прокрутки переместитесь вниз до тех пор, пока не появится график. Прижмите область графика левой клавишей мыши и перетащите его вверх поближе к результатам.

Если график сжат или растянут по горизонтали, то кликните правой кнопкой по графику и во всплывающем меню выберите «Исходные данные». В появившемся окне нажмите на кнопку в поле «Диапазон». Левой клавишей мыши выделите ячейку с надписью «Число повторений», а затем нажмите клавишу Shift и, не отпуская ее, выделите последнюю значащую ячейку в колонке D. Для возврата в предыдущее окно нажмите кнопку возврата в окне «Исходные данные – Диапазон:».

После завершения редактирования графика, документ нужно распечатать на бумаге. Если к компьютеру, на котором Вы работаете, подключен принтер, то выберите из меню ФайлÞПредварительный просмотр и установите нужные параметры страницы. Окончательно убедитесь в том, что вид документа соответствует желанию, вставьте бумагу в принтер и нажмите кнопку Печать. В случае отсутствия принтера документ можно сохранить на дискете и распечатать его на другом компьютере.

Не сохраняя изменения, закройте файл Stat2.xls и вновь его откройте. С помощью клавиатуры замените исходные значения в колонках A и B значениями, полученными в эксперименте для 500 измерений суммарного излучения. Используя ранее описанный алгоритм, составьте новый документ для суммарного излучения.

Завершите работу с приложением Microsoft Excel и откажитесь от сохранения изменений. Следуйте дальнейшим инструкциям лабораторной работы.

Приложение II

Таблица 2 Критические точки распределения Пирсона.

Число степеней свободы f	Уровень значимости e
0.99	0.98	0.95	0.90	0.10	0.05	0.02	0.01
	0.020	0.040	0.103	0.211	4.605	5.991	7.824	9.210
	0.115	0.185	0.352	0.584	6.251	7.815	9.937	11.345
	0.297	0.429	0.711	1.064	7.779	9.488	11.668	13.277
	0.554	0.752	1.145	1.610	9.236	11.070	13.388	15.086
	0.872	1.134	1.635	2.204	10.645	12.592	15.033	16.812
	1.239	1.564	2.167	2.833	12.017	14.067	16.622	18.475
	1.646	2.032	2.733	3.440	13.362	15.507	18.168	20.090
	2.088	2.532	3.325	4.168	14.684	16.919	19.679	21.666
	2.558	3.059	3.940	4.865	15.987	18.307	21.161	23.209
	3.053	3.609	4.575	5.578	17.275	19.675	22.618	24.725.
	3.571	4.178	5.226	6.304	18.549	21.026	24.054	26.217
	4.107	4.765	5.892	7.042	19.812	22.362	25.472	27.688
	4.660	5.368	6.571	7.790	21.064	23.685	26.873	29.141
	5.229	5.985	7.261	8.547	22.307	24.996	28.259	30.578
	5.812	6.614	7.962	9.312	23.542	26.296	29.633	32.000
	6.408	7.255	8.672	10.085	24.769	27.587	30.995	33.409
	7.015	7.906	9.390	10.865	25.989	28.869	32.346	34.805
	7.633	8.567	10.117	11.651	27.204	30.114	33.687	36.191
	8.260	9.237	10.851	12.444	28.412	31.410	35.020	37.566

Таблица 3.Критические точки распределения Колмогорова.

e	0.5	0.4	0.3	0.2	0.1	0.05	0.02	0.01	0.001
le	0.828	0.895	0.974	1.073	1.224	1.358	1.520	1.627	1.950

 

Приложение III

Распределение Пуассона.

Случайные величины принято описывать с помощью функции плотности распределения, которая определяет вероятность получения различных значений случайной величины из совокупности большого числа измерений этой величины.

Распределение редких событий, наблюдаемых в течение времени t, описывается дискретным распределением Пуассона:

, (15)

здесь параметр v характеризует среднюю интенсивность событий.

Параметры Пуассоновского распределения определяются следующими соотношениями;

(16)

где - средне число событий наблюдаемых в бесконечной серии измерений.

С учетом (16) равенство (15) имеет вид

. (17)

Из (17) следует, что функция плотности распределения Пуассона зависит только от одного параметра .

При малых значениях распределение Пуассона асимметрично относительно (см. рис. 3). При >>1 распределение практически совпадает с нормальным распределением со средним значением и дисперсией, равными . Практически это совпадение уже наблюдается при =20 (см. рис. 7)