Индексный метод изучения взаимосвязей. Система индексов
Индексный метод широко применяется для анализа роли отдельных факторов в динамике социально-экономического явления. Изменение количественной характеристики данного явления происходит под влиянием одного или нескольких факторов, выступающих как множителей совокупного результата.
Пример, динамика товарооборота в фактических ценах обусловлена совместным изменением как цены, так и количества проданных товаров. Индекс физического объема товарооборота и индекс цены выступают соизмерителями роли этих факторов на общее изменение размера товарооборота в фактических ценах.
Таким образом, чтобы образовать систему индексов, необходимо чтобы соизмерителями в индексах были разные уровни, причем это соизмерение получалось через произведение двух или нескольких индексов.
Системы индексов.
Индексы могут использоваться для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае для достижения сопоставимости они должны рассчитываться по единой схеме – системе индексов.
В зависимости от информационной базы и целей исследователя индексная система может строиться в четырех вариантах. Рассмотрим систему индексов на примере сводного индекса цен, рассчитываемого за «n» периодов:
1. Цепные индексы цен с переменными весами:
 ;
;  …
… 
1. Цепные индексы цен с постоянными весами:
 ;
;  …
… 
2. Базисные индексы цен с переменными весами:
 ;
;  …
… 
4.Базисные индексы цен с постоянными весами:
 ;
; 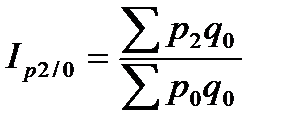 …
… 
Понятие о статистической и корреляционной связи. Задачи их анализа и моделирования.
Различают 2 типа связей меду различными явлениями и их признаком: функциональную и статистическую. Функциональной называется такая связь когда с изменением значения одной из
переменных вторая изменяется строго определенным образом, т.е., значению одной переменной соответствует одно или несколько точно заданных значений другой переменной. Функциональная связь возможна лишь в том случае, когда переменная у зависит от переменной х и не от каких других факторов не зависит, но в реальной жизни такое невозможно. Статистическая связь существует в том случае, когда с изменением значения одной из переменных вторая может в определенных пределах принимать любые значения, но ее статистические характеристики изменяются по определенному закону. Важнейший частный случай статистической связи – корреляционная связь. При корреляционной связи разным значениям одной переменной соответствуют различные средние значения другой переменной, т.е. с изменением значения
признака х закономерным образом изменяется среднее значение признака у.
Корреляционная связь может возникнуть разными путями:
- причинная зависимость вариации результативного признака от вариации факторного признака.
- Корреляционная связь может возникнуть между 2 следствиями одной причины (пожары, кол-во пожарников, размер пожара)
- Взаимосвязь признаков каждый из которых и причина и следствие одновременно(производительность труда и з/плата)
В статистике принято различать следующие виды зависимости:
- парная корреляция – связь между 2мя признаками результативным и факторным, либо между двумя факторными.
- Частная корреляция – зависимость между результативным и одним факторным признаком при фиксированном значении другого факторного признака.
- множественная корреляция – зависимость результативного признака от двух и более факторных признаков включенных в исследование.
Задачей корреляционного анализа является количественная оценка тесноты связи
между признаками.Регрессия исследует форму связи. Задача регрессионного анализа – определение аналитического выражения связи. Корреляционно-регрессионный анализ как общее понятие включает в себя изменение тесноты связи и установления аналитического выражения связи.






