Отметьте точки М, К, Р на ребрах АВ, ВС, D D параллелепипеда ABCDA B C D. постройте сечение параллелепипеда плоскостью МКР методами следа и внутреннего проецирования

 

6.1. метод следа(рис.7)

 

1.точки М и К лежат в плоскости сечения и в плоскости верхнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

2.продолжим прямую, на которой лежит сторона DC параллелепипеда. Прямые DC и

MK пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.

3.так как точка Р также принадлежит плоскости сечения и пересекает прямую СС в некоторой точке Х.

4.точки Х и Р лежат в одной плоскости грани DCC D. Соединим их и получим прямую ХР.

5.так как плоскости граней (противоположных) параллельны, то через точку Р можно провести прямую в грани DAA D, параллельную прямой КХ. Эта прямая пересечет сторону АА в точке Y.

6.Аналогично, проводим прямую YM, параллельно прямой РХ. Она совпадет с точкой М. построение сечения РYMKX сделано верно.

 

 

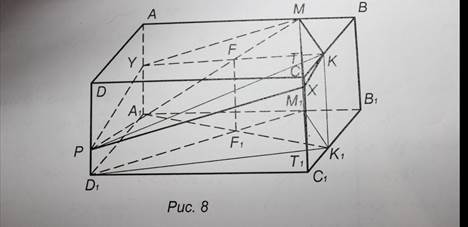
6.2. метод внутреннего проецирования.(рис.8)

 

1. отметим четырехугольник M K D A для нахождения точки пересечения сечения с гранью АА.
2. F -точка пересечения диагоналей четырехугольника M K D A
3. F- точка пересечения FF и РМ.
4. для определения Y соединяем F и К.
5. соединим Y и Р получаем отрезок PY.
6. Y соединяем с М, получаем YMю
7. отметим четырехугольник D M K C для нахождения точки пересечения сечения с гранью СС.
8. Т -точка пересечения диагоналей четырехугольника D M K C.
9. Т-точка пересечения Т Т и РК.
10. для определения Х соединим М и Т.
11. Соединяем К с Х и Х с Р. Получим PYMKX.

 

 

7.постройте сечение четырехугольной усеченной пирамиды плоскостью, проходящей через точку на верхнем основании, точку на нижнем основании и точку на боковом ребре.

 

Итак, имеем пирамиду АВСDA B C D и точки L,M,K(рис.9)

Построение плоскости сечения усеченной пирамиды будем производить методом внутреннего проецирования, как выше упоминалось.

1.для определения точки пересечения с ребром СС рассмотрим четырехугольник

D L MC.

2.F -точка пересечения диагоналей L C и D M.

3. Соединим F с центром проецирования S и на пересечении с диагональю КМ получим F.

4.продлеваем прямую (диагональ) LF до пересечения с ребром СС, получаем Х.

5. К и Х в одной плоскости, соединяем, и получаем сечение грани КN.

6. N и M в одной плоскости, соединяем и получаем сечение грани NP.

7.для определения точки пересечения с ребром АА рассмотрим четырехугольник A L MD

8. Т -точка пересечения диагоналей А М и D L.

9. соединим Т и центр проецирования S и на пересечении с диагональю KL получим точку Т.

10. продлеваем диагональ МТ до пересечения с ребром АА, получим Y.

11. К и Y в одной плоскости, соединяем и получим сечение грани К.

12. R и L в одной плоскости, соединяем и получаем сечение грани RH.

13.Н и С в одной плоскости, сединяем и получаем сечение грани НР.

14.сечение усеченной пирамиды построено KNPHR.

 

8.показать, что изображение является сверхполым. Каким оно является- верным или неверным?

 

Изображена пирамида SABC и изображено произвольное сечение пирамиды плоскостью.

Между тем, как мы знаем, изображение пирамиды полное. Для определения плоскости сечения достаточно знать три какие-либо определенные относительно тетраэдра SABC

Точки. Тогда по свойству полных изображений, четвертая точка сечения L вполне определяется и может быть построена, например, методом следа.

Точки K,N,M –определенные очевидно, так как лежат на гранях пирамиды. Отрезки MN и АВ лежат в одной плоскости. Найдем точку их пересечения Х. точки К и Х лежат в одной плоскости, соединяя их получим сечение грани KL.

Итак KL MN- действительное сечение пирамиды.

Значит исходное изображение пирамиды с сечением KLMN-сверхполное, неверное.

 

 

 

9.достроить изображение до изображения многогранника, имеющего только четырехугольные грани, точки А, В, С, D, E, F, G в качестве вершин и параллельные ребра DE,BG.

 

(Рис.11)

 

На основании многогранника АВСD построим диагонали BD и AC.

Точка пересечения F.

Соединим точки G и Е и в точке пересечения GЕ и FH получили точку F.

Соединим F и F до пересечения с ребром из точки С, еолучим Н.

Многогранник с гранями в форме четырехугольников и с ребрами DE и GB построен.

 

 

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное