АҚД-нің тұрақты (қозғалмайтын) өс төңірегінде айналғанда, оның өсте жатқан нүктелері қозғалмайды (4.5 суретіндегі АВ). Өс арқылы екі жазықтық жүргізейік – қозғалмайтын және денемен байланысып қозғалатын жазықтықты. Олардың арасындағы екі жақтық бұрышы дененің бұрылу бұрышы деп аталады, ол айналу өсінің оң бағыты жағынан қарағанда сағат тілінің қозғалысына қарсы болып көрінгенде, оң болып есептеледі. АҚД-нің тұрақты өс төңірегіндегі айналу заңы – келесі тәуелділік
= (t). (4.16)
Бұрыштық жылдамдық бұрышының уақыт өтуімен өзгеруін сипаттайды
= d/dt, яғни  . (4.17)
. (4.17)
Дененің бұрыштық жылдамдығын модулі || тең және айналу өсінің бойымен, ұшынан қарағанда дене сағат тілінің қозғалысына қарсы айналатын болып, бағытталған  векторымен кескіндеуге болады.
векторымен кескіндеуге болады.
Бұрыштық үдеу бұрыштық жылдамдығының уақыт өтуімен өзгеруін сипаттайды
= d/dt = d2 /dt2, яғни  . (4.18)
. (4.18)
Егер қозғалыс кезінде =const болса, айналу бірқалыпты деп аталады. (4.17) формуласын интегралдап, айналу заңын анықтаймыз
 (4.19)
(4.19)
Бірқалыпты айналу кезінде 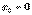 болса, онда
болса, онда
 . (4.19’)
. (4.19’)
Егер қозғалыс кезінде бұрыштық үдеу тұрақты болса(=const), айналу бірқалыпты айнымалы деп аталады, оның заңы келесі түрде жазылады
 . (4.20)
. (4.20)
Егер мен таңбалары бірдей болса, айналу – бірқалыпты үдемелі, әртүрлі болса, бірқалыпты кемімелі болады.
Айналатын дене нүктелерінің жылдамдықтары мен үдеулерін анықтаймыз (4.6 сурет).
Айналу кезінде М нүктесі радиусы h тең, жазықтығы айналу өсіне перпендикуляр және P центрі өсте жататын шеңберді кескіндейді. dt уақыт ішінде дене dφ бұрышына бұрылады, М нүктесі ds = h∙ dφ орын ауыстыру жасайды. Сонда
 . (4.21)
. (4.21)
Нүктенің үдеулерін анықтаймыз
 (4.22)
(4.22)
 үдеуі траекторияға жанама бағытталады (үдемелі айналу кезінде айналу бағытына сәйкес және кемімелі айналу кезінде айналу бағытына қарсы),
үдеуі траекторияға жанама бағытталады (үдемелі айналу кезінде айналу бағытына сәйкес және кемімелі айналу кезінде айналу бағытына қарсы),  үдеуі әрқашан МP радиусы бойымен өске қарай бағытталады. Нүктенің толық үдеуі
үдеуі әрқашан МP радиусы бойымен өске қарай бағытталады. Нүктенің толық үдеуі
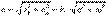 (4.23)
(4.23)
бұрышы(4.6 сурет) келесі тәуелдік арқылы анықталады
 . (4.24)
. (4.24)
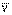 және
және  векторлары үшін келесі формулуларды шығаруға болады
векторлары үшін келесі формулуларды шығаруға болады
 , (4.25)
, (4.25)
 (4.26)
(4.26)
Динамика аксиомалары
Динамика деп материялық денелердің, олардың инерциясын есепке алуымен күштер әсерінен пайда болатын қозғалысын қарастыратын теориялық механиканың бөлімін атайды. Инерция деп материялық дененің өзінің қозғалыс немесе тыныштық қалпын күштер түспеген кезде сақтап қалу қасиетін айтады. Ілгерілемелі қозғалыстағы дененің инерциясының өлшемі болып табылатын зат мөлшеріне тәуелді физикалық шама дененің массасы m деп аталады.
Нүкте динамикасы 4 аксиомаға негізделеді.
1-аксиома (инерция заңы): күштер түспейтін материялық нүкте (МН), оған күштер түсіп, қалпын өзгерткенге дейін тыныштықта немесе бірқалыпты түзу сызықты қозғалыста болады. Күштер болмағандағы нүктенің қозғалысы инерциялық қозғалыс деп аталады. Инерция заңы орындалатын санақ жүйесі (СЖ) инерциялық СЖ деп аталады. Көптеген есептерде Жермен байланысқан СЖ инерциялық деп алынады.
2-аксиома (динамиканың негізгі заңы): МН-нің үдеуі оған түсетін күшке пропорционал және сол күшпен бағыттас. Динамиканың негізгі теңдеуі
 . (5.1)
. (5.1)
3-аксиома (әсер мен кері әсер заңы): екі МН бір-біріне модульдері тең және нүктелерді қосатын түзу бойымен қарама-қарсы бағытталған күштермен әсер етеді.
4-аксиома (күштер әсерінің тәуелсіздік заңы): әр күш бөлек түскенде МН алатын үдеулердің векторлық қосындысы барлық күштер біржолы түскенде алатын үдеуіне тең
 (5.2)
(5.2)
(5.2) теңдеуінің орнына (5.1) теңдеуін,  күші ретінде тең әсерлі күшті алып, қолдануға болады.
күші ретінде тең әсерлі күшті алып, қолдануға болады.
Ауырлық күш әсерінен денелер бірдей  үдеуіне ие болады, ол ауырлық күш үдеуі немесе еркін түсу үдеуі деп аталады. Егер МН-ге тек қана
үдеуіне ие болады, ол ауырлық күш үдеуі немесе еркін түсу үдеуі деп аталады. Егер МН-ге тек қана  ауырлық күші түсетін болса, онда (5.1) бойынша
ауырлық күші түсетін болса, онда (5.1) бойынша
 . (5.2)
. (5.2)
Дененің массасы оның орналасуына және оған түсетін күштерге тәуелсіз, ал дененің салмағы дене орнының географикалық еніне және оның Жер орталығына дейінгі қашықтығына тәуелді еркін түсу үдеуінің өзгеруімен өзгеріп тұрады.
5.2 Материялық нүкте қозғалысының дифференциалдық теңдеулері
МН {  } күштер жүйесінің әсерінен инерциалдық Оxyz санақ жүйесіне қатысты қозғалатын болсын, және күштер арасына байланыстардың реакциялары да кіреді деп есептейміз.
} күштер жүйесінің әсерінен инерциалдық Оxyz санақ жүйесіне қатысты қозғалатын болсын, және күштер арасына байланыстардың реакциялары да кіреді деп есептейміз.
(5.2) теңдеуін декарт координат өстеріне проекциялап, декарт координаттарындағы қозғалысының дифференциалдық теңдеулерін (ҚДТ) аламыз
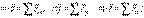 (5.3)
(5.3)
табиғи өстерге проекциялап, нүкте қозғалысының табиғи дифференциалдық теңдеулерін аламыз
 (5.4)
(5.4)
ҚДТ нүкте динамикасының екі негізгі есебін шешу үшін қолданылады:
1-негізгі есеп: нүкте қозғалысы бойынша оған түсетін күшті анықтау. Мұнда МН қозғалысының теңдеулерін дифференциалдап, нәтижелерін (5.3) немесе (5.4) теңдеулеріне қою керек, содан нүктеге түсетін күш анықталады;
2-негізгі есеп: нүктеге түсетін күштер бойынша оның қозғалысын анықтау. Мұнда жалпы жағдайда (5.3) немесе (5.4) дифференциалдық теңдеулерінің екінші интегралдарын табу керек. Дербес жағдайларда ҚДТ айнамалыларды бөлу әдісінің көмегімен интегралдалуы мүмкін.






