Расчётно-графическая работа по механике
Основные формулы.
Кинематика материальной точки
В Декартовой системе координат, используемой наиболее часто, положение точки А в данный момент времени характеризуется тремя координатами x, y, z или радиусом - вектором 
, проведенным из начала координат в данную точку (Рис. 1).
При движении материальной точки её координаты с течением времени изменяются. В общем случае её движение определяется скалярными уравнениями:
x = x(t), y = y(t), z = z(t) (1)
Эти уравнения эквивалентны векторному уравнению
(2)
где х, у, z – проекции радиуса-вектора на оси координат, а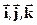 
- единичные векторы, направленные по соответствующим осям. Уравнения (1) и (2) называются кинематическими уравнениями движения материальной точки.
Мгновенная скорость в общем случае движения определяется первой производной от радиус-вектора по времени:
- вектор мгновенной скорости, 
Проекции скорости: 
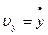
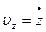
Мгновенное ускорение: 
Кинематика вращательного движения
Угловая скорость - векторная величина, характеризующая скорость вращения тела, численно равная первой производной псевдовектора угла поворота 
по времени t:
Угловое ускорение — векторная величина, характеризующая быстроту изменения угловой скорости твёрдого тела.
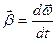
Тангенциальное (касательное) ускорение 
(составляющая ускорения)
Нормальное (центростремительное) ускорение (составляющая ускорения) - векторная величина, характеризующя изменение направления скорости:
Модуль полного ускорения:
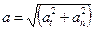
Динамика вращательного движения
Основное уравнение динамики вращательного движени ( Второй закон Ньютона)
,
где: 
-вектор импульса.
Основное уравнение динамики вращательного движения твердого тела
(1)
где 
- суммарный момент внешних сил, приложенных к телу относительно оси вращения; J - момент инерции тела относительно той же оси; 
- угловое ускорение.
В динамике вращательного движения различают два понятия: момент силы относительно точки и момент силы относительно оси вращения.
Момент силы относительно точки О определяется как векторное произведение
,
где 
- сила, 
- радиус-вектор, проведенный из точки О, в точку приложения силы.
Момент силы относительно оси вращения есть проекция 
на произвольную ось z, которая проходит через точку О:
.
Где l – плечо силы, то есть кратчайшее расстояние от оси до линии действия силы.
Момент инерции тела
или
,
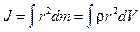где D mi - масса элемента; ri - расстояние от элемента до оси вращения; r - плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения. Таким образом, задача нахождения момента инерции сводится к интегрированию.
Для расчетов моментов инерции относительно произвольной оси может быть использована теорема Штейнера. Согласно ей, момент инерции J относительно произвольной оси равен сумме момента инерции тела Jc относительно оси, проходящей через центр инерции тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями.
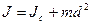
Момент импульса 
материальной точки определяется как векторное произведение
,
где m - масса материальной точки, 
- ее скорость,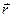 
-расстояние от точки до оси вращения.
Величина момента импульса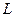 
материальной точки равна
L=m v r
Момент импульса твердого тела, вращающегося вокруг некоторой оси равен
,
где J – момент инерции тела, w -угловая скорость.
Закон сохранения момента импульса: в замкнутой системе суммарный момент импульса всех тел этой системы остается постоянным.
Кинетическая энергия вращающегося тела выражается формулой
Примеры решения и оформления задач.
Пример 1. Уравнение движения материальной точки вдоль оси имеет вид х = А + Вt + Ct 3, где А = 2 м, В = 1 м/c, C = -0,5 м/с 3. Найти координату х, проекцию мгновенной скорости и ускорения точки в момент времени t = 2 с.
| Дано: | Решение |
| А = 2 м | Координату х найдем, подставив в уравнение движения численные значения коэффициентов А, В и С и времени t: х = (2 + 1× 2 – 0,5× 23) = 0. Проекция мгновенной скорости на ось х определяется как первая производная от координаты по времени |
Vх = 
= B + 3 C× t 2.
Проекцию ускорения точки найдем, взяв первую производную от проекции скорости по времени
aх = 
= 6 C× t
Проверка размерности
[ Vх ] =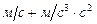 
= 
, [ а ]= 
= 
.
Подставляем числовые значения в момент времени t = 2 с
Vх = (1 – 3×0,5×22) м/c = -5 м/c,
aх = 6×(–0,5)×2 м/c 2 = -6 м/c 2.
Ответ: в момент времени t = 2 с проекция скорости материальной точки равна -5 м/c, проекция ускорения: -6 м/c 2.
Пример 2. Из пущенной с поверхности Земли вертикально вверх ракеты вырывается вниз струя газа со скоростью 
относительно ракеты. Начальная масса ракеты с топливом равна 
, ежесекундный расход топлива равен 
(кг/с). Определить ускорение ракеты через время 
после старта, считая поле тяготения однородным.
Решение
Выберем неподвижную систему отсчета, связанную с Землей. В соответствии с условием задачи масса ракеты непрерывно уменьшается, и основное уравнение динамики необходимо использовать в виде обобщённого второго закона Ньютона. Запишем его в проекции на вертикальную ось 0у. Пусть 
- масса ракеты в произвольный момент времени 
- ее скорость в тот же момент. Для выбранного момента времени импульс ракеты равен 
Спустя время 
масса ракеты станет равной 
а скорость 
. Соответственно импульс ракеты примет значение 
Кроме того, выброшенная порция газа (которая тоже принадлежит рассматриваемой системе) в выбранной системе отсчета станет обладать импульсом - 
Тогда изменение импульса системы
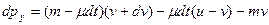
и соответственно, уравнение (1.13) в проекции на ось 0у принимает вид
(*)
Раскроем скобки:
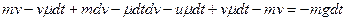
и после сокращений получим
Величины и 
стремятся к нулю. Поэтому произведение исключаем как бесконечно малую величину высшего порядка. С учетом этого соотношение (*) преобразуем к виду
После деления на получим
(**)
где 
- искомое ускорение ракеты. Запишем (**) в проекции на ось Оу:
(***)
Это уравнение аналогично второму закону Ньютона. Однако масса здесь не постоянна, и дополнительное слагаемое 
может быть истолковано как реактивная сила. Уравнение (***) является частным случаем уравнения Мещерского для движения точки с переменной массой. Для заданного момента времени формула для ускорения имеет вид
Замечание. Интегрируя это уравнение, можно получить зависимость скорости ракеты от времени, а затем и закон движения.
Пример 3. Водометный двигатель катера выбрасывает назад струю воды со скоростью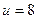 
м/с относительно катера. Расход воды в его турбине 
кг/с. Пренебрегая сопротивлением движению катера, определить его скорость 
в спокойной воде через 
с после начала движения. Масса катера 
т.
Решение
Выберем систему отсчета, связанную со спокойной водой, ось координат 
– вдоль направления движения катера. Пусть в некоторый момент времени скорость катера равна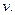 
Масса катера 
не изменяется, внешние силы отсутствуют, проекция относительной скорости поступающей в турбину воды равна - 
Уравнение движения запишем в проекции на ось :
или 
Введем безразмерную переменную 
Тогда 
и после замены и разделения переменных получим
Аналогичное уравнение рассматривалось в примере 1. Интегрируем это уравнение:
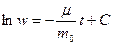или 
(*)
Из начального условия 
находим 
и приводим уравнение (*) к виду
Используя определение логарифмической функции, получим
или 
(**)
График этой функции приведен на рис.2. Скорость асимптотически стремится к предельному значению 
В этом случае скорость выбрасываемой струи воды в выбранной системе отсчета равна нулю, т.е. 
, и ускорения не будет.
Рис. 2
Подставив из условия с в выражение (**) и выполнив вычисления, получим ответ 
м/с.
