| Поступательное движение | Вращательное движение | ||
| Кинематика | |||
| Путь |  
| Угол поворота |  
|
| Скорость | 

| Угловая скорость |  
|
| Ускорение | 
| Угловое ускорение | 
|
 ; ;  ; ;  ; ;  ; ;  ; ; 
| |||
| Динамика | |||
| Основное уравнение динамики поступательного движения | 
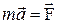
| Основное уравнение динамики вращательного движения | 

|
| Импульс | 
| Момент импульса | 
|
| Закон сохранения импульса | 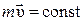
| Закон сохранения момента импульса | 
|
| Работа | 
| Работа вращения | 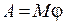
|
| Мощность | 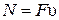
| Мощность | 
|
| Кинетическая энергия | 
| Кинетическая энергия вращ. тела | 
|
1.7. Теория тяготения Ньютона
Все тела в природе взаимно притягивают друг друга. Это взаимодействие называется гравитационным и является одним из фундаментальных взаимодействий в природе. Мы знаем о нем очень мало, гораздо меньше, чем, например, об электромагнитном взаимодействии. Тем не менее, на уровне механики мы можем описать гравитацию.
1.7.1. Закон всемирного тяготения: сила, с которой два тела притягиваются друг к другу, пропорциональна произведению масс этих тел и обратно пропорциональна квадрату расстояния между ними (рис.1.30):
 или
или 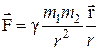 ,
,
где  гравитационная постоянная, равная
гравитационная постоянная, равная  м3/кг
м3/кг  с2;
с2;  и
и  – масса первого и второго тела; r – расстояние между телами.
– масса первого и второго тела; r – расстояние между телами.
1.7.2. Потенциальная энергия тела массы т, расположенного на расстоянии r от большего тела массы М (рис 1.48):
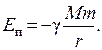

| 
|
| Рис. 1.48 |
1.7.3. Работа по перемещению тела массы m в гравитационном поле тела M (рис. 1.48):

1.7.4. Вектор напряжённости поля тяготения численно равен силе действующей со стороны поля на материальную точку единичной массы и совпадает с этой силой по направлению (рис. 1.49).
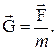
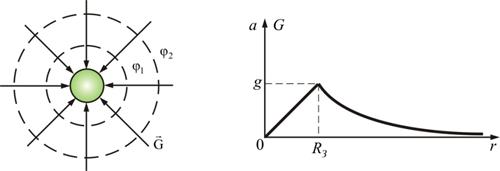
Зависимость напряженности от расстояния показано на рис. 1.50.
| |
| Рис. 1.49 | Рис. 1.50 |
1.7.5. Теорема о циркуляции векторов  и
и  :
:
 и
и  .
.
Работа консервативных сил, при перемещении тела вдоль замкнутого контура L тождественно равна 0.
1.7.6. Потенциал поля тяготения – величина, равная отношению потенциальной энергии Е п материальной точки к массе т:
 .
.
На рисунке 1.49 показаны эквипотенциальные поверхности  и линии напряженности
и линии напряженности  .
.
1.7.7. Взаимосвязь между потенциалом поля тяготения и его напряжённостью:
 .
.
1.7.8. Потенциальная энергия тела массой т на расстоянии r от Земли:
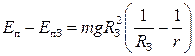 ,
,
где 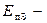 потенциальная энергия гравитационного поля на поверхности Земли;
потенциальная энергия гравитационного поля на поверхности Земли;  радиус Земли.
радиус Земли.
1.7.9. Полная энергия тела в гравитационном поле:
 .
.
1.8. Законы Кеплера
1.8.1. Первый закон Кеплера:Все планеты движутся по эллипсам, в одном из фокусов которого находиться Солнце (рис. 1.51).
1.8.2. Второй закон Кеплера: радиус вектор планеты описывает в равные промежутки времени равные площади (рис. 1.52):
 .
.

| 
|
| Рис. 1.51 | Рис. 1.52 |
1.8.3. Третий закон Кеплера: квадраты времен обращения планет относятся как кубы больших полуосей их орбит:
 , или
, или 
где Т – период обращения; R – радиус орбиты.
1.8.4. Первая космическая скорость – это скорость движения тела по круговой орбите вблизи поверхности Земли (рис. 1.53):
 .
.

|
| Рис. 1.53 |
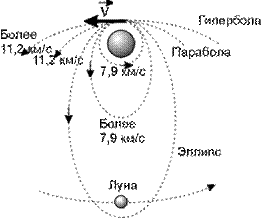
1.8.5. Вторая космическая скорость – это минимальная скорость, которую нужно сообщить телу на поверхности Земли, чтобы оно, преодолев земное притяжение, стало искусственным спутником Солнца (рис. 1.54):
 .
.
| 
|
| Рис. 1.54 |
1.8.6. Третьей космической скоростью называется скорость, при которой тело может покинуть пределы Солнечной системы, преодолев притяжение Солнца:
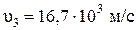 .
.
1.9. Механика жидкостей и газов
1.9.1. Давление жидкости на дно и стенки сосуда:
 ,
,
где F – сила, действующая на поверхность S.
1.9.2. Уравнение неразрывности для несжимаемой жидкости (рис. 1.55, 1.56):


| 
|
| Рис. 1.55 | Рис. 1.56 |
1.9.3. Уравнение Бернулли:

где  плотность жидкости; h – высота, на которой расположено сечение; Р – статическое давление жидкости для определенного сечения трубки тока.
плотность жидкости; h – высота, на которой расположено сечение; Р – статическое давление жидкости для определенного сечения трубки тока.
В качестве примеров применения уравнения Бернулли можно привести установку для измерения скорости течения жидкости (рис. 1.57), или устройство для измерения скорости самолета – трубку Пито (рис. 1.58).

| 
|
| Рис. 1.57 | Рис. 1.58 |
1.9.4. Подъемная сила крыла самолета: профиль крыла самолета (рис. 1.59) имеет такую форму, что скорость обтекающего потока воздуха относительно крыла внизу меньше, а вверху больше: υ2 > υ1. Поэтому давление над крылом меньше, чем под крылом: Р 1 > Р 2. Это приводит к избыточной силе  , которую можно разложить на две составляющие: подъемную силу
, которую можно разложить на две составляющие: подъемную силу  п и силу сопротивления
п и силу сопротивления 

|
| Рис. 1.59 |
1.9.5. Закон сообщающихся сосудов: в сообщающихся сосудах уровни однородных жидкостей, считая от наиболее близкой к поверхности земли точки (рис. 1.60), равны:
 .
.
1.9.6. Давление столба жидкости на глубине h:
 .
.
В сообщающихся сосудах, заполненных разнородными жидкостями с плотностью  , давления жидкостей на одном уровне одинаковы (рис. 1.60):
, давления жидкостей на одном уровне одинаковы (рис. 1.60):
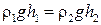 .
.

|
| Рис. 1.60 |
1.9.7. Закон Архимеда: на тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной телом жидкости:
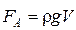 ,
,
где FA – выталкивающая сила; V – объем вытесненной жидкости.
1.9.8. Формула Торричелли, позволяющая определить скорость истечения жидкости из малого отверстия в открытом широком сосуде:
 ,
,
где h – глубина, на которой находится отверстие относительно
уровня жидкости в сосуде.
1.9.9. Формула Стокса, позволяющая определить силу сопротивления, действующую на медленно движущийся в вязкой среде шарик:
 ,
,
где r – радиус шарика;  – скорость шарика;
– скорость шарика;  коэффициент вязкости.
коэффициент вязкости.
1.9.10. Формула Пуазейля, позволяющая определить объем жидкости, протекающий за время t через капиллярную трубку длиной l:
 ,
,
где R – радиус трубки; 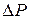 – разность давлений на концах трубки.
– разность давлений на концах трубки.
1.9.11. Поверхностное натяжение (рис. 1.61):
 или
или 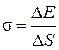 ,
,
где F – сила поверхностного натяжения, действующая на контур, ограничивающий поверхность жидкости; 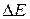 – поверхностная энергия, связанная с площадью
– поверхностная энергия, связанная с площадью  поверхности пленки; l – длина контура, ограничивающего поверхностный слой жидкости.
поверхности пленки; l – длина контура, ограничивающего поверхностный слой жидкости.
1.9.12. Формула Лапласа, позволяющая определить избыточное давление для произвольной поверхности жидкости двоякой кривизны:
 ,
,
где  и
и  – радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости; радиус кривизны положителен, если центр кривизны находится внутри жидкости (выпуклый мениск), и отрицателен (рис. 1.56), если центр кривизны вне жидкости (вогнутый мениск). Для сферической поверхности:
– радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости; радиус кривизны положителен, если центр кривизны находится внутри жидкости (выпуклый мениск), и отрицателен (рис. 1.56), если центр кривизны вне жидкости (вогнутый мениск). Для сферической поверхности:
 .
.

| 
|
| Рис. 1.61 | Рис. 1.62 |
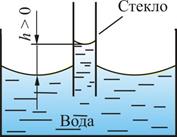
1.9.13. Высота подъема жидкости в капиллярной трубке (рис.1.61):
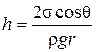 ,
,
где  – краевой угол; r – радиус капилляра;
– краевой угол; r – радиус капилляра;  – плотность жидкости.
– плотность жидкости.
1.9.14. Насыщенный пар – пар, находящийся в термодинамическом равновесии со своей жидкостью. Скорость преобразования пара равна скорости конденсации.
Давление насыщенного пара при данной температуре – максимальное давление, которое может иметь пар над жидкостью при этой температуре.
Давление насыщенного пара не зависит от жидкости объема сосуда, в котором находится пар. При изотермическом уменьшении объема насыщенного пара, часть пара переходит в жидкость, давление насыщенного пара при этом не меняется.
1.9.15. Относительная влажность воздуха – процентное отношение плотности (парциального давления) водяного пара в воздухе к плотности (парциальному давлению) насыщенного пара при той же температуре: φ = ρ/ρ (н) ∙ 100% или φ = p/p(н) ∙ 100%,
где ρ, ρ (н) – абсолютная влажность ненасыщенного и насыщенного водяного пара; p,p(н) – парциальное давление ненасыщенного и насыщенного водяного пара соответственно.
1.9.16. Абсолютная влажность воздуха – величина, равная плотности ρ водяного пара в воздухе или равная парциальному давлению P водяного пара:
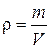 или
или  ,
,
где ρ – абсолютная влажность (плотность) водяного пара, m – масса водяного пара в объеме V, µ – молярная масса воды, P – парциальное давление водяного пара.
1.9.17. Точка росы – температура, при достижении которой ненасыщенный водяной пар становится насыщенным в результате изохорического охлаждения.
1.10. Специальная теория относительности
Г. Галилей установил, что во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму: в этом заключается суть механического принципы относительности. Противоречия между этим принципом и уравнениями электродинамики привело к отказу от преобразований Галлилея и созданию специальной теории относительности (СТО), являющейся предметом этой главы.
1.10.1. Принцип относительности Галилея: Законы природы, определяющие изменение состояния движения механических систем, не зависят от того, к какой из двух инерциальных систем отсчета они относятся.
1.10.2. Преобразования Галилея (рис. 1.63):
 ,
,  ,
,  ,
,  или
или  .
.
1.10.3. Закон сложения скоростей в классической механике (рис. 1.64):
 .
.

| 
|
| Рис. 1.63 | Рис. 1.64 |
1.10.4. Постулаты Эйнштейна:
· все законы природы одинаковы во всех инерциальных системах отсчета (принцип ивариантности систем отсчета);
· скорость света в пустоте (максимально возможная скорость) одинакова во всех инерциальных системах отсчета и не зависит от скорости источника и приемника света.
1.10.5. Событие в механике определяется координатами и временем, где и когда оно произошло. Событие изображается мировой точкой в четырехмерном пространстве, на осях которого откладываются 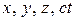 . Для простоты будем считать, что
. Для простоты будем считать, что  и в начальный момент событие произошло в мировой точке 0. (рис.) При изменении координат и времени мировая точка рисует мировую линию (рис. 1.65).
и в начальный момент событие произошло в мировой точке 0. (рис.) При изменении координат и времени мировая точка рисует мировую линию (рис. 1.65).
Абсолютно удаленные мировые точки не могут быть причинно связаны с событием 0, так как для попадания в них из 0 надо двигаться со скоростью, большей скорости света, что невозможно. Мировые точки, лежащие в конусах «абсолютное прошлое, будущее», могут быть причинно связаны с событием 0, являясь либо его причиной («абсолютное прошлое»), либо следствием («абсолютное будущее»).

|
| Рис. 1.65 |
1.10.6. Интервал  – характеризует свойства пространства-времени – расстояние между двумя мировыми точками (событиями):
– характеризует свойства пространства-времени – расстояние между двумя мировыми точками (событиями):
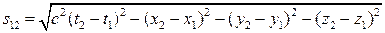 .
.
Если  , между событиями возможна причинная связь, а если
, между событиями возможна причинная связь, а если  , – невозможна. Интервал имеет одинаковое значение (т.е. инвариантен) в любой инерциальной системе отсчета.
, – невозможна. Интервал имеет одинаковое значение (т.е. инвариантен) в любой инерциальной системе отсчета.
1.10.7. Преобразования Лоренца (предполагается, что система отсчета К' движется со скоростью  в положительном направлении оси х системы отсчета К (рис. 1.46),причем оси х' и х совпадают, а оси у' и у и z' и z параллельны; с – скорость распространения света в вакууме):
в положительном направлении оси х системы отсчета К (рис. 1.46),причем оси х' и х совпадают, а оси у' и у и z' и z параллельны; с – скорость распространения света в вакууме):

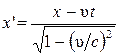 ,
,






1.10.6. Следствия из преобразований Лоренца:
· Интервал времени между событиями (рис. 1.66):
 .
.
· Лоренцево сокращение длины стержня (рис. 1.67, 1.68):
 ,
,
где  – собственная длина стержня;
– собственная длина стержня;  – длина стержня, измеренная в системе отсчета, относительно которой он движется со скоростью
– длина стержня, измеренная в системе отсчета, относительно которой он движется со скоростью  .
.

| 
| |
| Рис 1.66 | Рис 1.67 | |
· Релятивистское замедление времени (рис. 1.52):
 ,
,
где τ – собственное время;  промежуток времени между двумя событиями, отсчитанный покоящимися часами (рис. 1.69).
промежуток времени между двумя событиями, отсчитанный покоящимися часами (рис. 1.69).

| 
|
| Рис 1.68 | Рис 1.69 |
· Релятивистский закон сложения скоростей:







