Произвольное движение абсолютно твердого тела можно представить в виде суммы двух движений: поступательного и вращательного.
Поступательное движение — движение, при котором все точки тела движутся по одинаковым траекториям. В этом случае движение тела можно рассматривать как движение материальной точки.
Вращательное движение — движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой, называемой осью вращения тела.
Изменение положения тела в пространстве при вращательном движении определяется углом поворота  тела относительно некоторого начального положения.
тела относительно некоторого начального положения.
Угловая скорость  равна первой производной от угла поворота
равна первой производной от угла поворота  тела по времени t:
тела по времени t:

Угловое ускорение ε равно первой производной от угловой скорости  тела по времени t:
тела по времени t:

Если материальная точка движется по окружности радиуса  с постоянной угловой скоростью
с постоянной угловой скоростью  , то ее угловые и линейные характеристики движения связаны соотношениями:
, то ее угловые и линейные характеристики движения связаны соотношениями:

Частные случаи вращательного движения.
· Равномерное вращение:
угловая скорость  ;
;
угловое ускорение ε = 0;
угол поворота изменяется по закону:  .
.
· Равнопеременное вращение:
угловое ускорение  ;
;
угловая скорость и угол поворота изменяются по законам:
 .
.
Знак ²+² соответствует равноускоренному, а знак ²─² — равнозамедленному вращению;  — угловая скорость тела в момент времени
— угловая скорость тела в момент времени 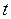 = 0.
= 0.
Период вращения  — время, в течение которого тело совершает один полный оборот.
— время, в течение которого тело совершает один полный оборот.
Частота вращения  — число оборотов, совершаемых телом за единицу времени.
— число оборотов, совершаемых телом за единицу времени.
Связь между периодом, частотой и угловой скоростью:
 ,
, 
Динамика материальной точки
Основное уравнение динамики материальной точки (второй закон Ньютона):

где  — равнодействующая сила, действующая на материальную точку;
— равнодействующая сила, действующая на материальную точку;  — импульс,
— импульс, 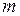 — масса,
— масса, 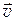 — скорость материальной точки.
— скорость материальной точки.
Если масса тела постоянна, то
 ,
,
где  — ускорение, приобретаемое телом массой
— ускорение, приобретаемое телом массой 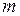 под действием силы
под действием силы  .
.
Закон Гука:
F упр = ─ k D x,
где F упр — сила упругости; k — коэффициент упругости или жесткость пружины; D x — изменение длины пружины. Знак ²─² означает, что сила упругости направлена против изменения длины пружины.
Закон трения скольжения:
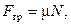
где F тр — сила трения скольжения;  – сила реакции опоры;
– сила реакции опоры; 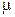 – коэффициент трения скольжения.
– коэффициент трения скольжения.
Сила тяжести:

где m — масса тела;  – ускорение свободного падения.
– ускорение свободного падения.
Изменение импульса тела равно импульсу приложенных к нему сил:

Закон сохранения импульса: в изолированной системе векторная сумма импульсов входящих в нее тел остается постоянной:

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
1. Координата материальной точки меняется по закону:  Найти перемещение, путь и среднюю скорость движения материальной точки за время t = 2 c после начала движения. Построить график зависимости координаты от времени. A = 1 м; ω = π рад/с.
Найти перемещение, путь и среднюю скорость движения материальной точки за время t = 2 c после начала движения. Построить график зависимости координаты от времени. A = 1 м; ω = π рад/с.
Решение:
График зависимости координаты  от времени t имеет вид:
от времени t имеет вид:

Рис. 1
Величина перемещения материальной точки вдоль оси 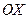 равна:
равна:
 .
.
где  — координата точки в начальный момент времени
— координата точки в начальный момент времени 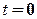 , а
, а  — в момент времени t = 2 c. Отсюда находим величину перемещения:
— в момент времени t = 2 c. Отсюда находим величину перемещения:
 .
.
Траекторией движения точки является отрезок прямой от –1 м до +1 м. Этот отрезок точка, как видно из графика (рис. 1), за время t = 2 c проходит дважды. Следовательно, путь  равен:
равен:

Средняя скорость движения по определению равна:

Здесь Δ S = S Δ t = t.
Поэтому: 
Ответ: 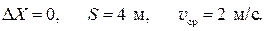
2. Камень брошен горизонтально с начальной скоростью 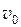 относительно поверхности земли. Найти уравнение траектории движения камня и радиус кривизны траектории в момент времени t.
относительно поверхности земли. Найти уравнение траектории движения камня и радиус кривизны траектории в момент времени t.
 Решение:
Решение:
Движение камня рассматриваем в системе отсчета, связанной с землей. Вдоль оси 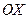 камень по условию задачи движется равномерно со скоростью
камень по условию задачи движется равномерно со скоростью  . Поэтому координата меняется по закону:
. Поэтому координата меняется по закону:
 (1)
(1)
Вдоль оси  камень падает с постоянным ускорением, равным ускорению свободного падения g. Поэтому скорость камня вдоль оси
камень падает с постоянным ускорением, равным ускорению свободного падения g. Поэтому скорость камня вдоль оси  равна
равна  gt, а координата
gt, а координата  меняется по закону:
меняется по закону:
 (2)
(2)
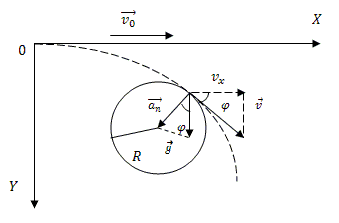
Рис. 2
Из уравнения (1) получаем:  .
.
Подставив 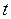 формулу (2), получим уравнение траектории движения камня:
формулу (2), получим уравнение траектории движения камня:

Радиус кривизны R траектории находим из определения нормального ускорения:
 ,
,
где  — полная скорость камня, равная
— полная скорость камня, равная

Отсюда получаем радиус кривизны траектории:
 . (3)
. (3)
Нормальное ускорение направлено к центру кривизны траектории перпендикулярно вектору полной скорости 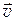 камня. С другой стороны, нормальное ускорение является составляющей полного ускорения, которое в данной задаче равно g. Из рис. 2 следует, что
камня. С другой стороны, нормальное ускорение является составляющей полного ускорения, которое в данной задаче равно g. Из рис. 2 следует, что
 , а
, а  . (4)
. (4)
Поэтому  .
.
Подставив (4) в (3), получаем:
 ,
,
или
 .
.
Ответ:  ,
,  .
.
2. Пушка стреляет под углом  к горизонту. Начальная скорость снаряда равна
к горизонту. Начальная скорость снаряда равна  . Найти максимальную высоту и дальность полета снаряда. Сопротивление воздуха не учитывать.
. Найти максимальную высоту и дальность полета снаряда. Сопротивление воздуха не учитывать.
Решение
Разложим вектор скорости  на составляющие вдоль осей координат
на составляющие вдоль осей координат 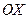 и
и  (см. рис. 3):
(см. рис. 3):  (1)
(1)

Рис.3
Движение снаряда вдоль оси  является равнопеременным, поэтому:
является равнопеременным, поэтому:
 , (2)
, (2)
 (3)
(3)
Снаряд поднимается вверх, пока вертикальная составляющая его скорости 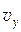 не станет равна нулю. Из уравнения (3) находим время подъема:
не станет равна нулю. Из уравнения (3) находим время подъема:
 (4)
(4)
Подставив (4) в (2), находим максимальную высоту подъема  :
:
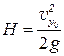 (5)
(5)
Снаряд, достигнув максимальной высоты подъема, опускается с ускорением свободного падения. Очевидно, что в этом случае:
 ,
,
где  — время падения снаряда.
— время падения снаряда.
Учитывая (4) и (5), получаем, что время падения снаряда равно времени его подъема. Полное время полета снаряда равно:
 (6)
(6)
За это время снаряд пролетит по горизонтали расстояние:
 . (7)
. (7)
Подставив (1) в формулы (5), (6), (7), находим высоту и дальность полета снаряда: 

Ответ: 

4. Вал токарного станка за 2 с приобретает угловую скорость ω = 628 рад/с. Считая вращение тела равноускоренным, найти угловое ускорение и число оборотов вала за это время.
Решение:
 Дано:
Дано:

 При равнопеременном вращении угол поворота тела и его угловая скорость меняются по закону:
При равнопеременном вращении угол поворота тела и его угловая скорость меняются по закону:

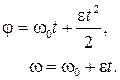
Из последнего соотношения: находим угловое ускорение:
 314 (рад/с2).
314 (рад/с2).
Угол поворота тела:
 628 (рад).
628 (рад).
Число оборотов тела:
 100 (оборотов).
100 (оборотов).
Ответ: 
6. Тело скользит по наклонной плоскости, составляющей с горизонтом угол θ. Зависимость пройденного телом пути  от времени
от времени  дается формулой
дается формулой 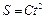 , где
, где  — константа. Определить коэффициент трения тела о плоскость.
— константа. Определить коэффициент трения тела о плоскость.
Решение:
При движении тела на него действуют три силы: сила тяжести  , сила реакции опоры
, сила реакции опоры 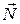 и сила трения
и сила трения  .
.

Рис. 4
Запишем основное уравнение динамики материальной точки (второй закон Ньютона) в виде:
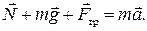
Выберем ось  вдоль направления скорости тела, ось
вдоль направления скорости тела, ось  — перпендикулярно ей, и спроецируем полученное уравнение динамики на эти оси:
— перпендикулярно ей, и спроецируем полученное уравнение динамики на эти оси:

Включим в эту систему уравнений закон трения скольжения

и формулу определения ускорения:

В результате получим:

Решая эту систему, получаем:

Ответ: 
5. Определить силу натяжения троса лебедки, поднимающей груз массой m с ускорением  .
.
Решение:
Расставим на рисунке силы, действующие на груз. Эти силы — сила тяжести  и сила натяжения троса
и сила натяжения троса  . Запишем основное уравнение динамики в векторном виде:
. Запишем основное уравнение динамики в векторном виде:
 .
.

Рис. 5
Спроецируем это уравнение на выбранную ось  :
:
 .
.
Решим полученное уравнение относительно  :
:

Ответ: 
10. Вагон массой m 1, движущийся со скоростью  , нагоняет вагон массой m 2, движущийся со скоростью
, нагоняет вагон массой m 2, движущийся со скоростью  . Найти скорость вагонов после сцепки.
. Найти скорость вагонов после сцепки.
Решение:
а) До сцепки суммарный импульс вагонов был:
 ,
,
б) После сцепки стал:
 .
.
По закону сохранения импульса:

или

Проецируя это уравнение на направление движения вагонов, получаем:


Рис. 6
Отсюда:

Ответ: 






