УДК 537.8
Кинематика поступательного и вращательного движения: метод. указания к практическим занятиям по физике /РГАСХМ ГОУ, Ростов н/Д, 2010. — 29 с.
Представляют собой руководство для проведения практических занятий и выполнения самостоятельных работ в 1-й части курса физики по темам: кинематика поступательного и вращательного движения; динамика материальной точки; закон сохранения импульса.
Дается необходимый теоретический и справочный материал, приведены примеры решения задач и задачи для самостоятельного решения.
Указания предназначены для студентов 1-го курса технических специальностей всех форм обучения.
Печатается по решению редакционно-издательского совета академии
| Рецензент | кандидат физико-математических наук, доцент | Э.Н. Кленов |
| Научный редактор | доктор технических наук, профессор | Д.Я. Паршин |
| Ó | Государственное образовательное учреждение высшего профессионального образования Ростовская-на-Дону государственная академия сельскохозяйственного машиностроения, 2010 |
Оглавление
| 1. | Краткие теоретические сведения | |
| 2. | Примеры решения задач | |
| 3. | Задачи для самостоятельного решения | |
| 4. | Обозначения и единицы физических величин в СИ | |
| 5. | Варианты заданий для самостоятельной работы | |
| 6. | Литература |
Краткие теоретические сведения
Кинематика материальной точки
Вектор перемещения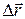 
— вектор, проведенный из начального 
в конечное положение 
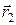материальной точки:
Путь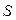 
— скалярная величина, равная расстоянию, пройденному материальной точкой вдоль траектории движения.
Средняя скорость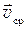 
— векторная величина, равная отношению вектора перемещения материальной точки к времени перемещения 
:
.
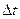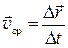Скорость перемещения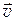 
(скорость) материальной точки — векторная величина, равная первой производной от радиус-вектора 
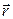материальной точки по времени t:
.
Вектор скорости направлен по касательной к траектории движения.
Средняя скалярная (путевая) скорость 
— скалярная величина, равная отношению пути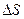 
, пройденного материальной точкой, к времени движения :
.
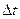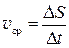Скалярная скорость 
(скорость движения) — скалярная величина, равная первой производной от пути S по времени t:
.
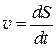Закон сложения скоростей: если тело участвует одновременно в двух движениях со скоростями 
и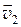 
, то его результирующая скорость:
. 
.
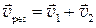Относительная скорость: если два тела движутся со скоростями и 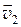относительно некоторой системы отсчета, то скорость 
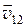первого тела относительно второго тела:
.
Ускорение 
материальной точки — векторная величина, равная первой производной от вектора скорости 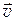по времени t:
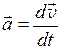
Вектор ускорения можно представить в виде суммы двух ускорений: нормального и тангенциального.
Нормальное ускорение характеризует быстроту изменения направления вектора скорости и равно отношению квадрата скорости к радиусу R кривизны траектории:
.
Нормальное ускорение направлено к центру кривизны траектории.
Тангенциальное ускорение характеризует быстроту изменения величины скорости и равно первой производной от величины скорости по времени t:
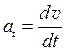
Тангенциальное ускорение направлено по касательной к траектории движения.
Абсолютная величина ускорения равна:
Частные случаи движения материальной точки.
· Прямолинейное движение:
нормальное ускорение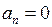 
.
· Равномерное движение:
величина скорости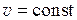 
;
тангенциальное ускорение 
;
путь 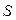изменяется по закону: 
.
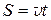· Равнопеременное движение:
тангенциальное ускорение 
;
путь S и скорость v изменяются по законам:
, 
.
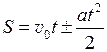Знак ²+² соответствует равноускоренному, а знак²─² — равнозамедленному движению;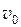 
— скорость тела в момент времени 
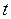= 0.
