Введение………………………………………………………….4
1. Кинематика…..............................................................................……..5
Основные формулы………………………………………………………5
Примеры решения задач…………………………………………………6
2. Динамика поступательного движения ….....................................….11
Основные формулы……………………………………………………..11
Примеры решения задач………………………………………………..12
3. Механика твёрдого тела.................................................................…20
Основные формулы……………………………………………………..20
Примеры решения задач………………………………………………..22
4. Механические колебания и волны....................................................29
Основные формулы……………………………………………………..29
Примеры решения задач………………………………………………..32
Список литературы……………………………………………………..38
Введение
Практические занятия являются одной из важнейших компонент учебного процесса по физике. Они способствуют приобщению студентов к самостоятельной работе, учат анализировать изучаемые физические явления, использовать на практике полученные теоретические знания.
Предназначены для студентов, изучающих раздел курса общей физики «Механика». В методических указаниях представлены примеры решения типичных задач разной степени трудности. Решения сопровождаются необходимыми примерами и комментариями. Задачи систематизированы по основным темам раздела. По каждой теме приведены основные формулы, облегчающие усвоение алгоритмов решения задач.
КИНЕМАТИКА
Основные формулы
Средняя скорость тела за промежуток времени Δ t определяется отношением перемещения тела Δ r к промежутку времени Δ t:
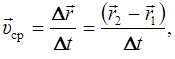
где 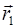 – радиус–вектор начальной точки,
– радиус–вектор начальной точки, 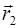 – конечной.
– конечной.
Средний модуль скорости тела за промежуток времени Δ t есть отношение пути S, пройденного телом за это время, к Δ t:
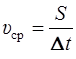 .
.
Средним ускорением называется отношение изменения скорости ко времени, за которое оно произошло:
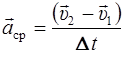 .
.
Мгновенная скорость 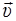 равна производной радиус-вектора точки по времени
равна производной радиус-вектора точки по времени 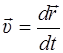
и направлена по касательной к траектории; для прямолинейного движения 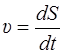 ,
,
ускорения 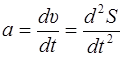 .
.
Кинематические соотношения для прямолинейного равнопеременного движения:
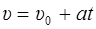 ,
,
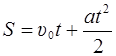 ,
,
где υ 0 скорость тела в момент времени t = 0, a – ускорение тела.
При криволинейном движении полное ускорение тела раскладывается на нормальную и тангенциальную к траектории составляющие: 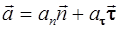 .
.
Тангенциальная составляющая ускорения определяет изменение модуля скорости: 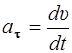 ,
,
нормальная – изменение направления скорости:
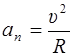 ,
,
где R –радиус кривизны траектории, нормальное ускорение направлено к центру кривизны траектории.
Модуль полного ускорения:
 .
.
При движении по окружности кинематическими характеристиками являются:
– угол поворота φ,
– угловая скорость ω = 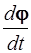 ,
,
– угловое ускорение ε=  =
= 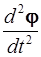 .
.
Кинематические уравнения для вращательного равнопеременного движения:
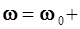 ε t
ε t
φ = ω0 t + ε 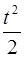 ,
,
где ω0 – угловая скорость в момент времени t =0, e – угловое ускорение.
Линейные и угловые параметры движения связаны соотношением: υ = ω R, a τ = ε R.
Примеры решения задач
Задача 1
Зависимость пройденного телом пути S от времени t даётся уравнением S=A+Bt+Ct 2 +Dt 3, где С =0,14 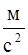 , D =0,01
, D =0,01 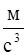 . Через какое время после начала движения ускорение тела будет равно 1
. Через какое время после начала движения ускорение тела будет равно 1 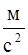 ? Чему равно среднее ускорение тела за время от t = 0 до t = 1
? Чему равно среднее ускорение тела за время от t = 0 до t = 1 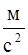 ?
?
Решение
Мгновенное ускорение тела в момент времени t можно найти как вторую производную от пути:
a = 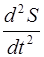 =
= 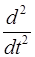 (B+ 2 Ct+ 3 Dt 2 ) = 2 C+ 6 Dt.
(B+ 2 Ct+ 3 Dt 2 ) = 2 C+ 6 Dt.
Надо определить значение t, при котором a = 1 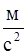 .
.
Получим: t = 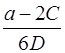 .
.
Подставив численные значения, получим:
t =  = 12 с.
= 12 с.
Чтобы найти среднее ускорение за промежуток времени от t 1 до t 2, надо определить величины скорости в момент времени t 1 и t 2 и их разность разделить на t 2– t 1:
a ср= 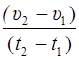 .
.
Скорость находим как производную пути по времени:
υ = B+ 2 Ct+ 3 Dt 2,
υ 1 = B+ 2 Ct 1 + 3 Dt 12,
υ 2 = B+ 2 Ct 2 + 3 Dt 22.
Разность скоростей:
υ 2– υ 1 = 2 С (t 2– t 1)+ 3 D (t 22 – t 12) = (t 2 – t 1)[2 С +3 D (t 2+ t 1)],
подставляем в формулу для среднего ускорения:
a ср = 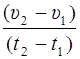 = 2 С+ 3 D (t 2+ t 1).
= 2 С+ 3 D (t 2+ t 1).
Подставив численные значения, получим:
a ср= 0,28 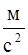 + 3.0,01
+ 3.0,01 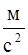 .1с = 0,31
.1с = 0,31 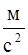 .
.
Задача 2
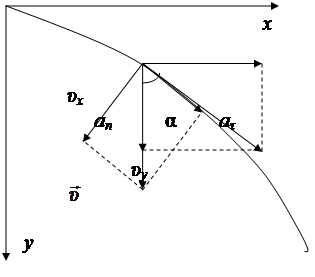
Тело брошено со скоростью υ 0 = 14,7 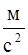 , под углом α = 30о к горизонту. Найти нормальное и тангенциальное ускорения тела через t = 1,25 с после начала движения, а также радиус кривизны траектории в данный момент времени. Сопротивление воздуха не учитывать.
, под углом α = 30о к горизонту. Найти нормальное и тангенциальное ускорения тела через t = 1,25 с после начала движения, а также радиус кривизны траектории в данный момент времени. Сопротивление воздуха не учитывать.
 Решение
Решение
|
Полная скорость тела направлена по касательной к траектории, её можно разложить на горизонтальную составляющую– υx и вертикальную составляющую – υy. Треугольники скоростей и ускорений прямоугольные и угол между υу и υ такой же, как и между a τ и g (так как a τ и υ направлены по касательной к траектории, а υy и g – по оси y). Таким образом, чтобы найти an и a τ, нужно определить в данный момент времени υx, υу, υ.
υx = υ 0 cos α = const,
υ у = - υ 0 sin α + gt
(так как мы выбрали направление оси y вниз),
υ = 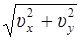 .
.
Из подобия треугольников имеем:
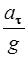 =
= 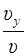 ,
,  =
=  ,
,
отсюда a τ = g 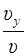 , an = g
, an = g  .
.
Радиус кривизны траектории определяется из условия:
an = 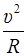 ,
,
значит R = 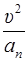 =
= 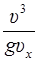 .
.
Подставив численные значения, получим:
aτ =  = 3,55
= 3,55  ,
,
an =  = 9,15
= 9,15 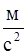 ,
,
R = 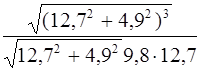 = 10 м.
= 10 м.
Задача 3
Колесо, вращаясь равнозамедленно, при торможении уменьшило свою скорость за 1 мин с 300 об/мин до 180 об/мин. Найти угловое ускорение колеса и число оборотов, сделанных им за это время.
Решение
Запишем кинематические соотношения для вращательного движения: ω = ω0 – ε t, φ = ω0 t – ε 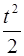 .
.
В условии задана не угловая скорость ω, а частота вращения ν, ω = 2πν, φ = 2π Ν.
Подставляем эти соотношения в уравнения:
2πν = 2πν0 – ε t.
Отсюда ε = 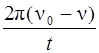 ,
,
2π Ν = 2π ν0 t – ε 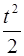 = 2πν0 t – 2π (ν0–ν)
= 2πν0 t – 2π (ν0–ν) 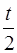 = 2π (ν0+ν)
= 2π (ν0+ν) 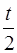 ,
,
или N = (ν0+ν) 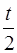 .
.
Подставив числовые значения, найдём:
ε = 750 мин -2 = 0,208 с -2,
N = 240 оборотов.
Задача 4
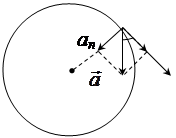
Найти угловое ускорение колеса, если известно, что через 2 с после начала равноускоренного движения вектор полного ускорения точки, лежащей на ободе, составляет угол 60о с направлением линейной скорости этой точки.
Решение
|
На чертеже видно, что an = a τ tg α. (1)
Выражаем an и aτ через угловые параметры движения:
an = ω2 R, a τ = ε R,
и подставляем в (1)
ω2 R = ε R tg α. (2)
При нулевой начальной скорости
ω = ε t.
Подставляем в (2):
ε2 t 2 = ε tg α,
ε = 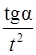 = 0,43 с-2.
= 0,43 с-2.
ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ
Основные формулы
Уравнение динамики поступательного движения тела:
 ,
,
где m – масса тела, 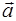 – его ускорение,
– его ускорение,  – сумма всех действующих на тело сил.
– сумма всех действующих на тело сил.
Импульсом тела называется произведение массы тела на его скорость: 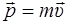 .
.
Закон изменения импульса:
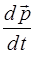 =
=  .
.
Работой силы F на перемещении ds называется произведение проекции силы на направление перемещения на это перемещение:
dA = Fs ds = Fds cosα,
где α – угол между направлениями силы и перемещения.
Работа переменной силы вычисляется как:
A =  .
.
Мощностью называют работу, произведенную за единицу времени: N =  .
.
Мгновенная мощность равна скалярному произведению силы, действующей на тело, на его скорость:
N = 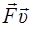 .
.
Кинетическая энергия тела при поступательном движении:
 ,
,
где m – масса тела, υ – его скорость.
Потенциальная энергия тела
– в однородном поле тяжести:
E п= mgh
(m – масса тела, g – ускорение свободного падения, h – высота тела над точкой, в которой потенциальная энергия принимается равной нулю);
– в поле упругих сил:
E п = 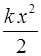
(k – коэффициент жесткости упругого тела, x – смещение от положения равновесия).
В замкнутой системе частиц полный импульс системы не меняется в процессе ее движения:
Σ 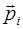 = const.
= const.
В замкнутой консервативной системе частиц сохраняется полная механическая энергия:
E = E k + E п = const.
Работа сил сопротивления равна убыли полной энергии системы частиц или тела: A conp = E 1 – E 2.
Примеры решения задач
Задача 5
Канат лежит на столе так, что часть его свешивается со стола, и начинает скользить тогда, когда длина свешивающейся части составляет 25% всей его длины. Чему равен коэффициент трения каната о стол?
Решение
Разрежем мысленно канат в месте сгиба и соединим обе части невесомой нерастяжимой нитью. Когда канат только начнёт скользить, все силы уравновесятся (так как он движется ещё без ускорения), а сила трения достигает величины силы трения скольжения, F тр = μ Ν.
Условия равновесия сил:
 mg = N
mg = N 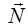
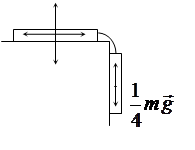 F тр = T
F тр = T 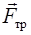

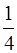 mg = T
mg = T 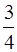 m
m 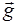

Отсюда: μ  mg =
mg = 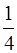 mg,
mg,
или μ = 
Задача 6

 |
Решение
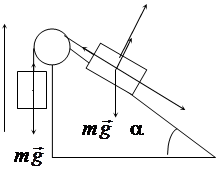 x y Запишем уравнения движения обоих тел:
x y Запишем уравнения движения обоих тел:
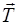
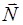 А: m
А: m 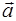 = m
= m 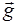 +
+ 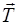

 x x x В: m
x x x В: m 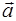 = m
= m 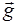 +
+ 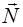 +
+ 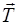
В проекциях для тела А:
– ma=T – mg (3)
Для тела В по оси х:
– ma = – T + mg sina (4)
0 = N – mg cos a (5)
Если сложить уравнения (3) и (4), то получим:
–2 ma = – mg + mg sin a,или
a = g 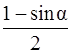
Подставив это значение, например, в уравнение (3) (можно в (4)), получаем: T = mg – ma = mg 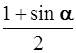
Подставляем числовые значения:
a = 9,8 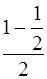 =
= 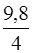 = 2,45
= 2,45 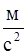
T = 1 ∙ 9,8 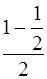 = 7,35 H
= 7,35 H
Задача 7
Вагон массой 20 т, двигавшийся равномерно, под действием силы трения в 6 кН через некоторое время остановился. Начальная скорость вагона равна 54 км/ч. Найти: 1) работу сил трения; 2) расстояние, которое вагон пройдёт до остановки.
Решение
Работа равна приращению кинетической энергии тела:
A тр = 0 – 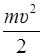 = –
= – 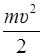 ,
,
Знак «–» означает, что работа сил трения отрицательна, так как силы трения направлены против движения.
С другой стороны, работу силы трения можно рассчитать через произведение силы на путь:
A тр = F тр. S,
отсюда S = 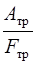 =
= 
Подставив числовые значения:
m = 2.104 кг, F тр = 6.103 Н, υ = 15 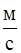 ,
,
получим:
A тр = 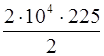 = 2,25.106 Дж = 2,25 МДж,
= 2,25.106 Дж = 2,25 МДж,
S = 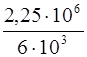 = 358 м.
= 358 м.
Задача 8
Камень бросили под углом α= 60о к горизонту со скоростью υ 0=15 м/с. Найти кинетическую, потенциальную и полную энергию камня: 1) спустя одну секунду после начала движения; 2) в высшей точке траектории. Масса камня m = 0,2 кг. Сопротивлением воздуха пренебречь.
Решение
Выберем ось х – по горизонтали, а ось у – по вертикали.
Проекции скорости:
 υx = υ 0cos a,(6)
υx = υ 0cos a,(6)
υ о υy = υ 0sin a – gt (7)
a x В момент времени t модуль скорости определится из соотношения:
υ 2 = υ 02 cos2 a + (υ 0sin a– gt)2= υ 02– 2 υ 0 gt sin a + g 2 t 2.
Высота камня над поверхностью земли в момент времени t определяется из соотношения:
h = υ 0 sin a - 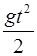 . (8)
. (8)
Находим кинетическую, потенциальную и полную энергию в момент времени t:
E k = 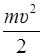 =
= 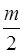 (υ 02– 2 υ 0 gt sin a + g 2 t 2),
(υ 02– 2 υ 0 gt sin a + g 2 t 2),
E п = mgh = 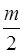 (2 υ 0 gt sin a – g 2 t 2),
(2 υ 0 gt sin a – g 2 t 2),
E = E k + E п = 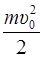 .
.
В высшей точке траектории υy = 0. Этой точки камень достигает за время 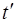 =
=  (из (7)), и максимальная высота подъёма h max=
(из (7)), и максимальная высота подъёма h max=  (из (8)).
(из (8)).
E k = 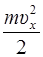 =
= 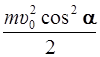 ,
,
E п = mgh max = 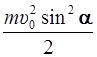 ,
,
E = E k+ E п = 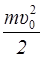 .
.
Подставляем числовые значения. В момент времени t = 1 c.
E k=17,4 Дж, E п = 5,1 Дж, E = 22,5 Дж.
В высшей точке траектории:
E k =16,9 Дж, E п = 5,6 Дж, E = 22,5 Дж.
Задача 9
На рельсах стоит платформа массой m 1 = 10 т, на платформе закреплено орудие массой m 2= 5 т, из которого проводится выстрел вдоль рельсов. Масса снаряда m 3= 100 кг, его начальная скорость относительно орудия υ 0 = 500 м/с. Определить скорость υx платформы в первый момент времени, если: 1) платформа стояла неподвижно, 2) платформа двигалась со скоростью υ 1= 18км/ч, и выстрел был произведён в направлении её движения, 3) платформа двигалась со скоростью υ 1= 18 км/ч, и выстрел был произведён в направлении, противоположном её движению.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы до какого-либо события (в данном случае выстрела) должен быть равен её импульсу после события. За положительное выбираем направление скорости снаряда. До выстрела вся система имела импульс (m 1+ m 2+ m 3) υ 1, после выстрела платформа с орудием движутся со скоростью υx, их импульс (m 1+ m 2) υx, а снаряд относительно земли движется со скоростью υ 0 + υ 1, его импульс m 3(υ 0+ υ 1). Закон сохранения импульса записывается так:
(m 1 + m 2 + m 3) υ 1 = (m 1 + m 2) υx + m 3(υ 0 + υ 1),
отсюда υx = 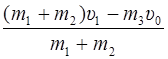 = υ 1 –
= υ 1 –  υ 0.
υ 0.
Подставляем значения масс, υ 1 и υ 0:
1) υ 1 = 0
υx = – 3,33 м/с.
Знак минус означает, что платформа с орудием движется противоположно направлению движения снаряда;
2) υ 1 = 18 км/ч = 5 м/с,
υx = 5 – 3,33 = 1,67 м/с.
Платформа с орудием продолжает двигаться в направлении выстрела, но с меньшей скоростью;
3) υ 1 = – 18 км/ч = – 5 м/с
υx = – 5 – 3,33 = – 8,33 м/с.
Скорость платформы, двигавшейся в направлении, противоположном направлению выстрела, увеличивается.
Задача 10
Пуля, летящая горизонтально, попадает в шар, подвешенный на лёгком жёстком стержне, и застревает в нём. Масса пули в 1000 раз меньше массы шара. Расстояние от точки подвеса стержня до центра шара равно 1 м. Найти скорость пули, если известно, что стержень с шаром отклонился от удара на угол 10о.
Решение.
 Если пуля застревает в шаре, то удар
Если пуля застревает в шаре, то удар
абсолютно неупругий, и выполняется только закон сохранения импульса. До удара пуля имела импульс mυ, шар импульса не имел. Непосредственно после удара пуля с шаром имеют общую скорость υ 1, их импульс (M + m) υ 1.
Закон сохранения импульса:
m υ = (M + m) υ 1,
отсюда υ 1 =  υ.
υ.
Шар вместе с пулей в момент удара приобрёл кинетическую энергию:
E k = 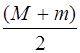 υ 12=
υ 12= 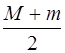
 υ 2=
υ 2= 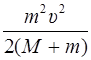 .
.
За счёт этой энергии шар поднялся на высоту h, при этом его кинетическая энергия переходит в потенциальную:
E k = E п Þ 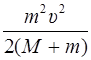 = (M + m) gh. (9)
= (M + m) gh. (9)
Высоту h можно выразить через расстояние от точки подвеса до центра шара и угол отклонения от вертикали
h = L – L cos a = L (1 – cos a).
Подставив последнее выражение в соотношение (9), получим:
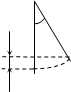 a L
a L 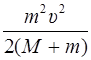 = gL (1 – cos a),
= gL (1 – cos a),
h и определим скорость пули:
υ =  .
.
Подставив числовые значения, получим:
υ = 1001 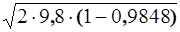 » 543 м/с.
» 543 м/с.
Задача 11
Камень, привязанный к верёвке, равномерно вращается в вертикальной плоскости. Найти массу камня, если известно, что разность между максимальным и минимальным натяжениями верёвки равны 9,8 Н.
 Решение
Решение
В верхней точке траектории и сила тяжести, и 
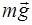 сила натяжения верёвки направлены вниз.
сила натяжения верёвки направлены вниз.
L Уравнение движения в верхней точке имеет вид:
|
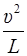 = mg + T 1.
= mg + T 1.
В нижней точке траектории сила тяжести направлена вниз, а сила натяжения верёвки и нормальное ускорение вверх. Уравнение движения в нижней точке:
man = m 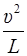 = T 2 – mg.
= T 2 – mg.
По условию камень вращается с постоянной скоростью, поэтому левые части обоих уравнений одинаковы. Значит, можно приравнять правые части:
mg + T 1 = T 2 – mg,
отсюда T 2 – T 1 = 2 mg,
m = 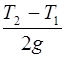 .
.
Подставляем числа: m = 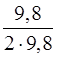 = 0,5 кг.
= 0,5 кг.
Задача 12
Шоссе имеет вираж с уклоном в 10° при радиусе закругления дороги в 100 м. На какую скорость рассчитан вираж?
Решение
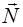 Сила, действующая на автомобиль, складывается
Сила, действующая на автомобиль, складывается
 из силы тяжести
из силы тяжести 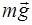 и силы нормального давления
и силы нормального давления 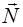 . Сумма этих сил обусловливает нормальное ускорение автомобиля при повороте.
. Сумма этих сил обусловливает нормальное ускорение автомобиля при повороте.
Из треугольника сил видно, что: 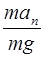 = tg a.
= tg a.
Рассчитаем an, сократив массу
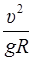 = tg a,
= tg a,
отсюда υ =  =41,5 м/с.
=41,5 м/с.
МЕХАНИКА ТВЕРДОГО ТЕЛА
Основные формулы
Мерой инертности твердого тела при вращательном движении является момент инерции:
I = Σ mi ∙ ri 2,
где mi – элементарная масса i – го кусочка тела, ri – расстояние этого кусочка от оси вращения.
Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:
Полый цилиндр I = m (R 12 + R 22).
Тонкий обруч I = mR 2.
Сплошной цилиндр I =  mR 2.
mR 2.
Шар I = 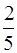 mR 2.
mR 2.
Тонкий стержень I = 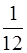 ml 2.
ml 2.
Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:
I = I 0 + ma 2,
где I – момент инерции тела относительно данной оси, I 0 – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, m – масса тела, а – расстояние между осями.
Основное уравнение динамики вращательного движения твердого тела: I e = M,
где I – момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.
Момент силы F равен: M = F l,
где l – расстояние от линии, вдоль которой действует сила, до оси вращения.
Момент импульса твердого тела относительно неподвижной оси: L = I ω,
где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.
Момент импульса материальной точки относительно неподвижной оси: L = m υ r,
где m – масса частицы, υ – ее скорость, r – расстояние от линии, вдоль которой движется частица, до данной оси.
В замкнутой системе частиц полный момент импульса не меняется: Σ Li = const.
Кинетическая энергия вращающегося тела:
E k = 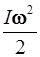 ,
,
где I – момент инерции тела, ω – его угловая скорость.
Кинетическая энергия катящегося тела:
E k = 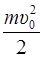 +
+  ,
,
где m – масса тела, υ 0 – скорость поступательного движения центра масс, I 0 – момент инерции тела относительно оси, проходящей через центр масс, ω – угловая скорость вращения тела.
Примеры решения задач
Задача 13
Прямой круглый однородный конус имеет массу m и радиус основания R. Найти момент инерции конуса относительно его оси.
Решение
 Разобьём конус на цилиндрические слои ось толщиной dr. Масса такого слоя
Разобьём конус на цилиндрические слои ось толщиной dr. Масса такого слоя
dm = rp r 2 dr,
где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя
dI = dm.r 2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I =  =
=  ρπ r 4 dr =
ρπ r 4 dr = 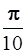 ρ R 5.
ρ R 5.
Остаётся выразить его через массу всего цилиндра:
m =  =
= 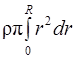 =
= 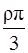 R 3,
R 3,
отсюда ρ = 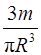 ,
,
I = 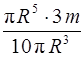 =
= 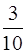 mR 2.
mR 2.
Задача 14
Маховое колесо, имеющее момент инерции 245 кг∙м2, вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Решение
При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.
ω 0 = 2 π ν 0, ω = 0,
0 = 2 π ν 0 - ε t,
отсюда ε = 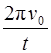 .
.
Это ускорение обусловлено действием момента сил трения
M тр = I ε = 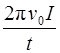 .
.
Полный угол поворота при равнозамедленном движении находится из соотношения:
φ = ω0 t - 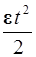 ,
,
φ =2π N, ω 0 = 2 π ν 0, ε = 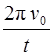 .
.
Перепишем соотношения для угла в виде:
2π N = 2 π ν 0 t - 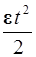 = 2 π ν 0 t -
= 2 π ν 0 t - 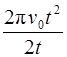 =
=  .
.
Для нахождения числа оборотов получим:
N = 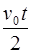 .
.
Подставив числовые значения, найдём:
M тр = 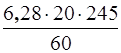 = 506 Нм,
= 506 Нм,
N =  = 600 об.
= 600 об.
Задача 15
На барабан радиусом R = 20 см, момент инерции которого равен I = 0,1 кг∙м2, намотан шнур, к которому привязан груз массой m = 0,5 кг. До начала вращения высота груза над полом равна h 1 = 1 м. Найти: 1) через какое время груз опустился до пола; 2) кинетическую энергию груза в момент удара о пол; 3) натяжение нити. Трением пренебречь.
Решение
|
 На груз действует сила тяжести mg и сила натяжения шнура Т. Уравнение поступательного движения груза ma = mg – T.
На груз действует сила тяжести mg и сила натяжения шнура Т. Уравнение поступательного движения груза ma = mg – T.
Барабан вращается вокруг неподвижной оси. Его уравнение движения M = I ε,
где М – момент силы натяжения шнура, М = TR, I – момент инерции барабана,ε =  – его угловое ускорение.
– его угловое ускорение.
TR = I  .
.
Выражаем отсюда силу натяжения шнура:
T = I 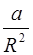 (10)
(10)
и подставляем ее в уравнение движения груза:
mg = a (m +  ) = am (1 +
) = am (1 + 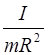 ).
).
Получаем ускорение груза:
a =  . (11)
. (11)
Время движения груза можно найти из уравнения:
h 1 =  ,
,
t = 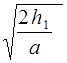 =
= 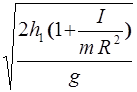 .
.
В момент удара о пол груз имел скорость:
υ = at = 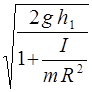 .
.
Следовательно, его кинетическая энергия:
E k =  =
= 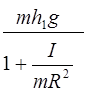 .
.
Подставив выражение для ускорения (11) в формулу (10), получим: T = 
 =
= 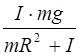 .
.
Подставив числовые значения, определим искомые величины:
t = 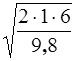 = 1,1 c,
= 1,1 c,
E k = 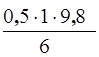 = 0,82 Дж,
= 0,82 Дж,
T = 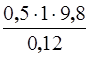 = 4,1 Н.
= 4,1 Н.
Задача 16
Шар массой m = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.
Решение
Кинетическая энергия катящегося тела равна:
E k =  +
+  . (12)
. (12)
Момент инерции шара I =  ,
,
угловая скорость вращения w = 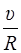 .
.
Подставляем эти величины в формулу (12):
E k =  +
+ 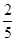
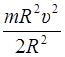 =
=  m υ 2.
m υ 2.
Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:
Q = E k1 – E k2 =  m υ 12 -
m υ 12 -  m υ 22 =
m υ 22 =  m (υ 12 - υ 22).
m (υ 12 - υ 22).
Подставив числовые значения, получим:
а =  ∙1(100∙10-4 – 64.10-4) =
∙1(100∙10-4 – 64.10-4) =  10-4 = 2,25∙10-3 Дж = 2,52 МДж.
10-4 = 2,25∙10-3 Дж = 2,52 МДж.
Задача 17
Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m 1 = 3 кг. Колеса считать тонкими обручами.
Решение
Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.
E k =  +
+ 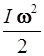 .
.
Момент инерции колес, представляющих собой тонкие обручи, равен I = 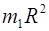 ,а угловая скорость вращения w =
,а угловая скорость вращения w = 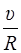 .
.
Подставляем эти значения в выражение для кинетической энергии: E k =  +
+ 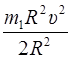 =
= 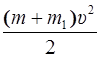 .
.
Скорость надо перевести в м/с: υ = 2,5 м/с.
Подстановка числовых значений дает: E k =253 Дж.
Задача 18
Однородный стержень длиной 85см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Решение
Чтобы стержень смог сделать полный оборот вокруг оси, он должен подняться до вертикального положения В.
Если отсчитывать потенциальную энергию стержня от начального положения А, то в положении В центр масс его поднят на
высоту С 2- С 1= l – длина стержня. Стержень приобретает потенциальную энергию Е n = mgℓ за счет кинетической энергии,
 В которую ему сообщили в положении А. Если
В которую ему сообщили в положении А. Если
υ – наименьшая скорость нижнего конца, при которой он сможет сделать полный оборот, то
угловая скорость стержня w =  .
.
Момент инерции стержня относительно оси, проходящей через его конец, определятся по теореме Штейнера:
I = 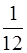 m l 2 = m
m l 2 = m  =
=  m l 2,
m l 2,
где 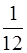 ml 2–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс,
ml 2–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс, 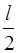 – расстояние от центра масс до требуемой оси.
– расстояние от центра масс до требуемой оси.
Кинетическая энергия вращательного движения:
E k = 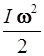 =
=  .
.  =
= 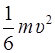 .
.
По закону сохранения энергии, кинетическая энергия стержня в положении А равна его потенциальной энергии в положении В:
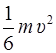 = mgl,
= mgl,
отсюда υ = 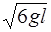 .
.
Подставляем числовые значения: υ = 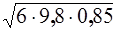 »7 м/с.
»7 м/с.
Задача 19
Человек массой m 1 = 60 кг находится на неподвижной платформе массой m = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиуса 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.
Решение
 Первоначально платформа с человеком покоилась,
Первоначально платформа с человеком покоилась,
момент импульса этой системы был равен нулю. Когда человек начнет двигаться по платформе, платформа будет вращаться в противоположном направлении. Если расстояние от человека до оси вращения платформы r, в месте нахождения человека u = w r. Таким образом, если человек движется относительно платформы со скоростью
υ, то относительно земли он будет двигаться со скоростью υ – w r, его момент импульса относительно оси платформы L 1 = m 1(υ – w r) r. Момент импульса платформы относительно ее оси:
L = – I w,
где I – момент инерции платформы.
Поскольку платформа представляет собой однородный диск, то ее момент инерции относительно оси, проходящей через центр:
I =  mR 2.
mR 2.
Запишем закон сохранения момента импульса для данной системы:
O = L 1 + L = m 1(υ – w r) r –  mR 2w,
mR 2w,
отсюда можно определить угловую скорость вращения платформы:
w =  .
.
Число оборотов платформы в минуту определится из соотношения:
n =  60 =
60 = 
 .
.
Подстановка числового значений дает:
n = 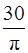
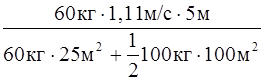 = 0,49 об/мин.
= 0,49 об/мин.






