Воздуха методом адиабатического расширения

Физика

Механика

 

 

«Определение коэффициента Пуассона для воздуха

методом адиабатического расширения»

 

 

Методические указания к лабораторной работе №11 для направления подготовки

 

 

специалистов:	130400.65	- Горное дело
	190109.65	- Наземные транспортно-технологические средства
бакалавров:	080200.62	- Менеджмент
	140400.62	- Электроэнергетика и электротехника
	220400.62	- Управление в технических системах
	270800.62	- Строительство
	190600.62	- Эксплуатация транспортно-технологических машин и комплексов

 

Губкин, 2011

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ

имени В.С. Черномырдина»

Губкинский институт (филиал)

 

УТВЕРЖДЕНО

Директором Губкинского

института (филиала) МГОУ

 

Физика

Механика

 

«Определение коэффициента Пуассона для воздуха

методом адиабатического расширения»

 

 

Методические указания к лабораторной работе №11 для направления подготовки

 

 

специалистов:	130400.65	- Горное дело
	190109.65	- Наземные транспортно-технологические средства
бакалавров:	080200.62	- Менеджмент
	140400.62	- Электроэнергетика и электротехника
	220400.62	- Управление в технических системах
	270800.62	- Строительство
	190600.62	- Эксплуатация транспортно-технологических машин и комплексов

 

 

Губкин, 2011

УДК 53

Ф 50

 

Физика. Часть 1. Определение коэффициента Пуассона для воздуха методом адиабатического расширения: Методические указания к лабораторной работе №11 / Сост. А.Н.Ряполов; Рец. д.ф.-м.н., профессор, зав. кафедрой физики КГТУ В.М. Полунин, к.т.н., профессор кафедры "Теоретической и прикладной механики" ГИ(филиала) МГОУ А.И. Гарбовицкий.- Губкин.: МГОУ, 2011.- 9 с.

 

Методические указания включают рекомендации и указания по выполнению лабораторной работы, в которой определяется коэффициент Пуассона для воздуха методом адиабатического расширения.

Указания содержат краткую теоретическую часть; описание экспериментальной установки, порядок выполнения работы, контрольные вопросы и указана литература по теории.

Предназначены для студентов технических специальностей вузов.

 

© Губкинский институт (филиал) Московского государственного открытого университета, 2011.

 

© А.Н. Ряполов, 2011.

ЛАБОРАТОРНАЯ РАБОТА 11

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ПУАССОНА ДЛЯ

ВОЗДУХА МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ

 

Цель работы: определить коэффициент Пуассона для воздуха эксперименталь­ным путем; расширить и углубить представление о первом начале термодинамики, законах идеального газа.

Приборы и принадлежности: стеклянный баллон, насос, манометр, наручные часы.

I.Теоретическое введение

Теплоемкость газов. Состояние газа может быть охарактеризовано тремя вели­чинами - параметрами состояния: давлением р, объемом V и температурой Т. Урав­нение состояния идеального газа связывает эти величины. Для одного моля газа оно имеет вид:

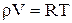(1)

где R -молярная газовая постоянная.

Теплоемкость тела равна количеству теплоты, которую нужно сообщить телу, чтобы нагреть его на 1 Кельвин. По определению теплоемкости имеем

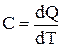(2)

Величина теплоемкости газов зависит от условий нагревания. Выясним эту за­висимость, воспользовавшись уравнением состояния (1) и первым началом термоди­намики, которое можно сформулировать следующим образом: количество теплоты dQ, переданное системе, затрачивается на увеличение ее внутренней энергии dU и на работу dА, совершаемую системой против внешних сил,

По определению теплоемкости

(3)

Из уравнения (3) видно, что теплоемкость может иметь различные значения в зависимости от способов нагревания газа, так как одному и тому же значению dТ могут со­ответствовать различные значения dU и dA.

Элементарная работа dA=pdV.

Рассмотрим основные процессы, протекающие в идеальном газе при изменении температуры, когда масса газа остается неизменной и равной одному молю. Количе­ство теплоты, необходимое для нагревания одного моля газа на 1°К, определяется молярной теплоемкостью.

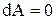Изохорический процесс. Процесс называется изохорическим, если объем тела при изменении температура остается постоянным, т.е. V = const. В этом случае: .Следовательно, и , т.е. при этом вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (3) следует, что молярная те­плоемкость газа при постоянном объеме равна

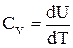(4)

Изобарический процесс. Процесс, протекающий при постоянном давлении ,называется изобарическим. Для этого случая формула (3) перепишется в виде:

(5)

Из уравнения газового состояния (1) получаем

(6)

Но 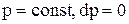. Следовательно, .Подставляя это выражение в уравне­ние (5) и заменяя dU через , получим окончательно уравнение Майера

С_р= С_v +R (7)

 

Изотермический процесс. Изотермическим процессом называется процесс, протекающий при постоянной температуре (Т= соnst).В этом случае dТ= 0,

dQ =dА, т.е. внутренняя энергия газа остается постоянной и все подводимое тепло расходует­ся на работу.

Адиабатический процесс. Процесс, протекающий без теплообмена с окру­жающей средой, называется адиабатическим. Первое начало термодинамики будет иметь вид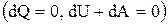

(8)

То есть при адиабатическом процессе расширения или сжатия работа соверша­ется газом только за счет изменения запаса внутренней энергии. Выведем уравнение адиабатического процесса (уравнение Пуассона).

Но 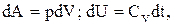значит,

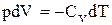(9)

Разделим уравнение (6) на (9) и, учитывая (7), получим

где .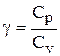

Интегрируя и потенцируя, получим уравнение Пуассона: