Рассмотрим суммарный момент импульса системы точек (тела) относительно некоторой точки О.

При переходе к другой точке О1 радиус-векторы точек системы преобразуются  , поэтому
, поэтому

Суммарный импульс системы равен импульсу центра масс 
 .
.
Поэтому в системе отсчета, где центр масс тела покоится  , суммарный момент импульса не зависит от точки, относительно которой он вычисляется.
, суммарный момент импульса не зависит от точки, относительно которой он вычисляется.
Если рассматривается движение твердого тела, то возможное движение в случае  – это вращение вокруг центра масс. В этом смысле момент импульса описывает вращательное движение системы (тела).
– это вращение вокруг центра масс. В этом смысле момент импульса описывает вращательное движение системы (тела).
Найдем производную от суммарного момента импульса
 .
.
Силы, действующие на точки системы, разделим на внутренние, действующие между точками системы и внешние – со стороны тел, не входящих в систему:  .
.
 .
.
Внутренние силы подчинятся третьему закону Ньютона - они лежат на прямых линиях, попарно соединяющих точки, противоположны по направлению и одинаковы по величине
 .
.
Для каждой из таких пар сил можно ввести одинаковое плечо  , поэтому
, поэтому
 .
.
Окончательно
 .
.
Уравнение динамики вращательного движения системы точек
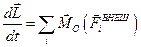 .
.
Производная от вектора суммарного момента импульса системы равна векторной сумме моментов внешних сил, действующих на систему.
Покоординатное равенство
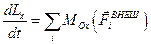 ,
,  ,
,  .
.
Момент импульса твердого тела.
Рассмотрим твердое тело, которое вращается вокруг неподвижной оси z с угловой скоростью w. Выделим в теле малую частицу массой D mi. Найдем момент импульса этой частицы относительно некоторой точки О на оси вращения. Если радиус-вектор частицы 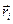 , вектор импульса
, вектор импульса  , то вектор момента импульса частицы
, то вектор момента импульса частицы  приложен к точке О и направлен перпендикулярно к векторам
приложен к точке О и направлен перпендикулярно к векторам 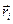 и
и  , т.е. под некоторым углом bi к оси z. Траекторией частицы Dmi является окружность, поэтому вектор импульса
, т.е. под некоторым углом bi к оси z. Траекторией частицы Dmi является окружность, поэтому вектор импульса  направлен по касательной к этой окружности. Следовательно, угол между векторами
направлен по касательной к этой окружности. Следовательно, угол между векторами 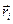 и
и  равен 900 (как угол между образующей и направляющей конуса). Тогда величина момента импульса частицы
равен 900 (как угол между образующей и направляющей конуса). Тогда величина момента импульса частицы  .
.
Пусть  - радиус окружности – траектории частицы. Тогда
- радиус окружности – траектории частицы. Тогда  . Рассмотрим проекцию вектора момента импульса на ось z:
. Рассмотрим проекцию вектора момента импульса на ось z:  .
.
Учитывая, что  , получаем:
, получаем:  .
.
Но  . Тогда
. Тогда

Для всего тела  .
.
 В это выражение входят параметры движения частиц, которые не зависят от положения точки О. Поэтому величина момента импульса вдоль оси z не зависит от положения точки на оси, для которой она вычисляется. В этом выражении величина
В это выражение входят параметры движения частиц, которые не зависят от положения точки О. Поэтому величина момента импульса вдоль оси z не зависит от положения точки на оси, для которой она вычисляется. В этом выражении величина

называется моментом инерции твердого тела относительно оси z (единица измерения кг×м2). Для сплошных тел суммирование можно заменить интегралом по массе тела
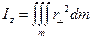 .
.






