Лекция 3. Закон сохранения момента импульса.
Момент силы. Момент импульса материальной точки и механической системы. Уравнение моментов механической системы. Закон сохранения момента импульса механической системы.
Математические сведения.
Векторным произведением двух (ненулевых) векторов 
и 
называется вектор 
, который в декартовой системе координат (с ортами 
, 
, 
) определяется по формуле
.
Величина 
(площадь прямоугольника на векторах 
и 
).
Свойства векторного произведения.
1) Вектор 
направлен перпендикулярно к плоскости векторов и . Поэтому для любого вектора 
, лежащего в плоскости (линейно независимых) векторов и (т.е. 
), получаем 
. Следовательно, если два ненулевых вектора и параллельны, то 
.
2) Производная по времени от векторного произведения – это вектор 
.
Действительно, (базисные векторы , , - постоянные) 
Вектор момента импульса
Вектором момента импульса относительно точки О называется вектор
,
где 
- радиус-вектор из точки О, 
- вектор импульса точки. Вектор 
направлен перпендикулярно к плоскости векторов и 
. Точку О иногда называют полюсом. Найдем производную от вектора момента импульса по времени
.
Первое слагаемое в правой части: 
. Так как в инерциальной системе отсчета по второму закону Ньютона (в импульсной форме) 
, то второе слагаемое имеет вид 
.
Величина 
называется вектором момента силы 
относительно точки О.
Окончательно получаем:
производная от вектора момента импульса относительно точки равна моменту действующих сил относительно этой точки.
Свойства вектора момента силы.
1) 
и 
.
2) В декартовых координатах
.
3) Момент суммы сил равен сумме моментов каждой из сил 
.
4) Сумма моментов сил относительно точки
при переходе к другой точке О1, при которой 
изменится по правилу
.
Следовательно, момент сил не изменится, если 
.
5) Пусть 
, где 
, 
тогда 
.
Следовательно, если две одинаковые силы лежат на одной прямой, то их моменты одинаковые. Эта прямая называется линией действия силы . Длина вектора 
называется плечом силы относительно точки О.
Момент силы относительно оси.
Как следует из определения момент силы, координаты вектора моменты силы относительно координатных осей определяются формулами
, 
, 
.
Рассмотрим метод нахождения момента силы относительно некоторой оси z. Для этого надо рассмотреть вектор момента силы относительно некоторой точки О на этой оси и найти проекцию вектора момента силы на эту ось.
1) Проекция вектора момента силы на ось z не зависит от выбора точки О.
Возьмем на оси z две разные точки О1 и О2 и найдем моменты силы F относительно этих точек.
, 
.
Разность векторов 
направлена перпендикулярно вектору 
, лежащему на оси z. Следовательно, если рассмотреть орт оси z – вектор 
, то проекции на ось z равны между собой
.
Поэтому, момент силы относительно оси z определен однозначно.
Следствие. Если момент силы относительно некоторой точки на оси равен нулю, то равен нулю момент силы относительно этой оси.
2) Если вектор силы параллелен оси z, то момент силы относительно оси равен нулю 
.
Действительно вектор момента силы относительно любой точки на оси должен быть перпендикулярен вектору силы, поэтому он также перпендикулярен и оси, параллельной этому вектору. Поэтому проекция вектора момента силы на эту ось будет равна нулю. Следовательно, если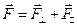 
разложение вектора силы на компоненту 
параллельную оси, и компоненту 
, перпендикулярную оси, то
.
3) Если вектор силы и ось не параллельны, но лежат в одной плоскости, то момент силы относительно оси равен нулю. Действительно, в этом случае вектор момента силы относительно любой точки на оси направлен перпендикулярно этой плоскости (т.к. вектор тоже лежит в этой плоскости). Можно сказать и иначе. Если рассмотреть точку пресечения линии действия силы и прямой z, то момент силы относительно этой точки равен нулю, поэтому и момент силы относительно оси равен нулю.
Итак, чтобы найти момент силы относительно оси z, надо:
1) найти проекцию силы на любую плоскость p перпендикулярную этой оси и указать точку О - точку пересечения этой плоскости с осью z;
2) найти плечо силы относительно оси – т.е. расстояние от линии действия проекции силы l (в плоскости p) до точки О (длину отрезка ОА на рисунке);
3) найти величину момента силы 
и направление по правилу правого винта (буравчика).
Правило правого винта в данном случае: вектор момента силы вдоль оси направлен так, что вектор задает вращение в плоскости p вокруг точки О по часовой стрелке.
4) Если на оси z указано положительное направление (говорят, что ось ориентирована), то указать знак проекции момента силы.
