Какой бы хорошей ни была теплоизоляция калориметра, при калориметрических измерениях нельзя избежать теплообмена с окружающей средой. Предлагаемый метод учета теплообмена сводится к замене реального процесса фазового перехода, длящегося конечное время, идеализированным «мгновенным» процессом поглощения тепла льдом.
Графический метод учета теплообмена основан на эмпирическом законе Ньютона, который заключается в том, что скорость теплопередачи пропорциональна разности температур системы t и среды t ср, если эта разность невелика:
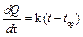 , при (t – t ср) <10, , при (t – t ср) <10,
| (12.8) |
где k – коэффициент теплопередачи, τ – время. В результате теплообмена с окружающей средой система либо получает теплоту при t ср > t, либо отдает при t ср < t. Условимся отданное количество теплоты считать положительным, а полученное отрицательным.
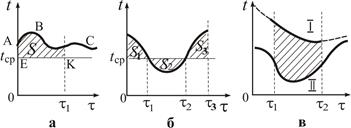
Это количество теплоты можно представить графически. Действительно, рассмотрим график зависимости температуры некоторой системы от времени – кривая АВС на рис. 12.1а. Пусть температура среды при этом остается постоянной и изображается графически прямой (температура системы больше температуры среды).
|
| Рис. 1 |
Теплота, отданная системой за время от 0 до τ1, в соответствии с законом Ньютона равна
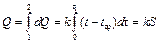 . .
| (12.9) |
Интеграл в уравнении (12.9) численно равен площади на графике, ограниченной кривой АВС, прямой ЕК, осью ординат и прямой τ = τ1 (заштрихованная площадь). Следовательно, теплота, отданная в среду, пропорциональна этой площади.
 В случае, когда в ходе процесса температура системы принимает значения и большие, и меньшие температуры среды, количество теплоты, отданное системой за время от 0 до τ3 (рис. 1б) можно представить так:
В случае, когда в ходе процесса температура системы принимает значения и большие, и меньшие температуры среды, количество теплоты, отданное системой за время от 0 до τ3 (рис. 1б) можно представить так:
В случае, когда t < t ср, соответствующую площадь надо брать со знаком «-» (участок, лежащий под прямой t = t ср).
Пользуясь графическим методом, можно оценить разность отданных в среду количеств теплоты для процессов, происходящих в одинаковых условиях теплообмена, т. е. с одинаковым коэффициентом k (например, процессы, происходящие в одном и том же калориметре при постоянной температуре неизменной среды). Заштрихованная площадь на рис. 1в показывает, на сколько больше теплоты отдано в среду в ходе процесса I по сравнению с процессом IIза время от τ1 до τ2, так как
  . .
|
Если в системе не происходит других процессов, кроме теплообмена с окружающей средой, и характер изменения температуры в некотором интервале времени (τ1, τ2) известен, то закон Ньютона позволяет экстраполировать (однозначно предсказать) ход зависимости t = f( τ ) на области τ < τ1 и τ > τ2 (рис. 12.1в).
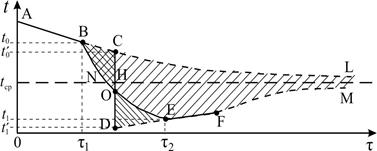
Рассмотрим процессы, происходящие при плавлении льда в калориметре, и изобразим графически зависимость температуры нашей системы (калориметр со льдом) от времени (рис. 12.2).
Проведем опыт следующим образом. Возьмем калориметр со льдом, имеющий температуру приблизительно на 10°С выше комнатной. На начальном этапе от моментаτ = 0 до τ = τ1 происходит понижение температуры системы за счет теплообмена с внешней средой – участок АВ. В момент τ1 в калориметр опустим лед, имеющий температуру 0°С. Льда необходимо взять столько, чтобы при его плавлении температура системы опустилась ниже температуры среды. Интервал времени от τ1 до τ2 – основная стадия опыта (участок BNE), за это время происходит плавление льда. Начиная с момента τ2, температура системы будет повышаться в результате получения тепла извне – на графике участок EF.
Ординаты точек В и Е есть соответственно температура воды в калориметре в момент опускания льда (t0) и в момент окончания плавления (t 1). Кривая ABNEF описывает реальный процесс, обозначим его I.
Экстраполируем участок графика АВ на область τ > τ1 линией BCL – так изменилась бы температура системы, если бы в калориметр не был положен лед (при τ→ ∞ температура системы стремится к температуре среды), обозначим этот процесс II.
Экстраполируем участок EF на область τ < τ2 и τ → ∞ - кривая DEFM – при τ → ∞ температура системы также стремится к температуре среды.
|
| Рис. 12.2 |
Площадь между кривыми ABCL и ABOEFM (заштрихована на рисунке), как видно из графического метода, показывает, на сколько I процесс отдал в среду теплоты меньше, чем II:
kS = Q I – Q II = Q. Так как в обоих случаях и вода (m 2), и калориметр (m 3) из одного и того же начального состояния с t = t 1 переходят в одно и то же конечное состояние с t = t ср, то в соответствии с первым началом термодинамики, можно утверждать, что это количество теплоты Q расходуется в системе на плавление льда и нагревание получившейся из него воды до температуры среды, т. е.
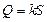  . .
|
Проведем вертикальную прямую СD так, чтобы площади SBCO и SОDЕ были равны. Получившийся график ACODEFM описывает некоторый идеализированный процесс, в котором от точки С происходит только теплообмен со средой, затем (CD) «мгновенный» фазовый переход, и затем (DEFM) – опять только теплообмен. Обозначим температуру в точке С – t 0' и в точке D – t 1' . Площадь S 1, ограниченная отрезком CH, прямой t = t сри кривой СL пропорциональна количеству теплоты, отданному в среду калориметром с водой при их остывании от t 0' до t ср, т.е.
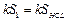  . .
|
Площадь S 2 ограниченная отрезком HD, прямой t = t ср и кривой DEFM пропорциональна количеству теплоты, полученному из среды при нагревании от t 1' до t ср калориметром с водой и водой, получившейся при плавлении льда, т.е.
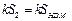 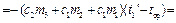 
|
Знак «-» указывает на то, что в этом случае система получала тепло из среды. Но по построению S 1 + S 2 = SODE - SOBC = S, следовательно
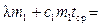 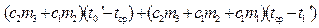 , ,
|
что после приведения подобных членов приводит к уравнению для определения удельной теплоты плавления льда:
 . .
|
Следовательно, для решения задачи необходимо определить величины t 0' и t 1', что делается с помощью экспериментального графика и описанных выше дополнительных построений.
Порядок выполнения работы
1. Взвесить внутренний калориметр и определить его массу m к (масса мешалки m м написана на ней самой).
2. Наполнить внутренний калориметр примерно на 2/3 водой, температура которой примерно на 10°С выше комнатной. Взвесить сосуд еще раз, определив, тем самым, массу воды m 2.
3. Собрать калориметрическую установку, вставив внутренний калориметр во внешний и поместив термометр в воду для измерения температуры во время опыта. Перемешать воду в калориметре.
4. Подготовить кусок льда, масса которого m 1 примерно равна 1/3 массы воды, и t = 00C.
5. Включить секундомер, зафиксировав температуру в начальный момент времени. Тщательно перемешивая воду, записывать в таблицу показания термометра через 1 – 2 минуты до тех пор, пока температура воды в калориметре за счет теплообмена с внешней средой понизится примерно на 0,8 – 1,5°С (4 – 10 значений). Это начальная стадия опыта.
6. зафиксировав температуру t 0, опустить в калориметр, заранее приготовленный и высушенный фильтровальной бумагой, кусок льда.
7. Продолжая перемешивать воду в калориметре, измерять температуру в нем как можно чаще (через 15 -20 секунд) до тех пор, пока не кончится процесс плавления льда, что соответствует минимальной температуре t 1 в калориметре. Это главная стадия опыта.
8. В заключительной стадии опыта необходимо, продолжая перемешивать воду, отмечать через 1 -2 минуты повышение температуры воды в калориметре в результате теплообмена с внешней средой до тех пор, пока она не повысится на 1 – 2°С выше температуры t 1.
9. Взвесить внутренний калориметр в третий раз, чтобы определить массу льда m 1.
10. Построить на миллиметровой бумаге график зависимости температуры системы от времени по полученным экспериментальным данным. Проведя вертикальный отрезок СD (см. рис 12.2) так, чтобы площади DOC и DOE были равны, определить по графику исправленные значения температур t 0' и t 1'. Рассчитать значение величины λ по формуле (12.7) и величину изменения энтропии льда при плавлении (S 2 – S 1) по формуле (12.6).
11. Вычислить погрешности полученных значений ∆ λ и ∆ (S2 – S1).






