Краткая теоретическая часть

Кафедра физики

 

Методические указания к лабораторной работе № 2-мех.

ИЗУЧЕНИЕ ЗАКОНОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ С ПОМОЩЬЮ

МАЯТНИКА ОБЕРБЕКА»

 

 

Составили:

Горковенко А.И. Фатеев И.Г.

 

 

Тюмень 2004г.

ЛАБОРАТОРНАЯ РАБОТА № 2-мех.

ИЗУЧЕНИЕ ЗАКОНОВ-ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

С ПОМОЩЬЮ МАЯТНИКА ОБЕРБЕКА.

 

ЦЕЛЬ РАБОТЫ:	определение момента сил трения в опоре вала маят­ника Обербека и вычисление/его момента инерции.
ОБОРУДОВАНИЕ:	маятник Обербека, набор грузов, линейка, электри­ческий секундомер.

КРАТКАЯ ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Вращательным называется такое движение твердого тела, при ко­тором все точки тела движутся по окружностям, центры которых ле­жат на одной прямой, называемой осью вращения.

Вращательное движение характеризуется угловой скоростью w которая определяется как производная угла поворота j тела по времени t

,

и угловым ускорением e

.

Между линейными (s, v, a) и угловыми (j, w, e) характерис­тиками вращающегося тела имеется следующая связь:

S = j××r;	v = w×r;	an = w2×r,
			,
		at = e×r,

v - скорость и a - ускорение какой-либо точки вращающегося тела, S - пройденный ею путь, r - расстояние от точки до оси вращения, и a_t и a_n -тангенциальная и нормальная сос­тавляющие ускорения.

При вращательном движении тела его кинематические и динамические характеристики зависят от действующего на тело момента внеш­них сил и от момента инерции тела.

Если сила , действующая на тело, лежит в плоскости, пер­пендикулярной некоторой оси, то моментом М силы относительно этой оси называется величина, равная произведению силы F на ее плечо l,

M = F×l,

плечо l - кратчайшее расстояние от оси до линии действия силы.

В качестве примера на рис.1 показано плечо силы от­носительно оси, проходящей через точку 0 перпендикуляр­но плоскости рисунка.

Моментом инерции тела относительно какой-либо оси, называется сумма произведений масс точек тела на квадраты их расстояний до оси

,

m_i – масса i-той точки тела, r_i - расстояние от i -той точки до оси.

Основной закон динамики вращательного движения твердого тела заключается в том, что сумма 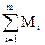моментов внешних сил, взятых относительно оси вращения, равна произве­дению момента инерции I тела относительно оси вращения на его угловое ускорение e

. (1)

Работа A совершаемая силами при вращении тела, равна произ­ведению момента M этих сил, взятому относительно оси вра­щения, на угол j поворота тела

A = M×j. (2)

 

 

ОПИСАНИЕ УСТАНОВКИ И ВЫВОД РАСЧЕТНЫХ ФОРМУЛ.

Маятник Обербека (рис.2) состоит из вала с двумя шкивами (1) и четырех неподвижно скрепленных с валом стержней (2) одинаковой длины. На концах стержней, на одинаковом расстоянии от оси вра­щения закреплены грузы в виде цилиндров (З). На один из шкивов наматывается нить (4), к свободному концу которой подвешивается груз Р. Под действием собственного веса груз будет двигаться вниз, вызывая вращение маятника. Обозначим за t время полно­го разматывания нити /высота груза над полом в момент времени t будет минимальна/. Путь, пройденный грузом за время t обозначим h₁. После полного разматывания нити, в результате вра­щения по инерции вала со стержнями, произойдет наматывание нити на шкив и груз поднимется, пройдя при этом расстояние h₂.

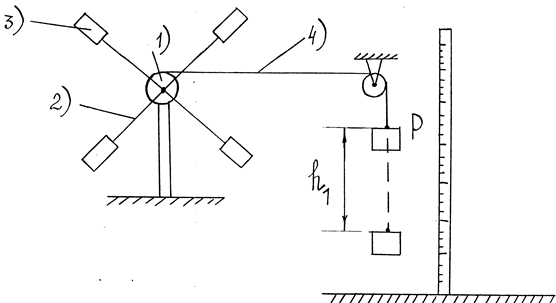
Рис.2.

По значениям перемещений h₁ и h₂, а также времени t можно вычислить момент инерции маятника Обербека. Уравнение, движения груза записывается

ma = mg - T, (3)

m - масса груза, a - его ускорение, T - сила натяжения нити, g - ускорение свободного падения.

Уравнение вращательного движения маятника, в соответствии с законом (1) имеет вид

I×e = T×r - M_тр., (4)

I - момент инерции маятника Обербека /шкивы, стержни, грузы на них/, r - радиус шкива, на который намотана нить, M_тр - момент сил трения, действующих в опоре вала.

Если при полном разматывании нити груз проходит расстояние h₁ за время t, то его ускорение

.

Подставляя величину ускорения в формулу (З), получаем натяжение T нити

. (6)

Из уравнения (4) следует, что момент инерции маятника

. (7)

Учитывая, что ускорение a груза и угловое ускорение e маят­ника связаны соотношением

a = e×r, (8)

получаем

(9)

Т к. массы шкивов, стержней и цилиндров на них, а также расстоя­ния этих масс до оси вращения неизменны, то момент инерции I вращающейся части установки должен оставаться величиной постоянной при любом изменении подвешиваемого груза.

Для определения момента сил трения в выражении (9), воспользу­емся законом сохранения энергии. Если груз, опущенный с высоты h₁, при последующем наматывании нити достигает высоты h₂ то согласно закону сохранения энергии

, (10)

j - угол поворота маятника при прохождении грузом расстояния h₁ + h₂,

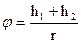. (11)

Тогда из уравнения (10), с учетом (11)

. (12)

Изменяя массу подвешиваемого груза Р и рассчитывая каждый раз a, T и М_тр по формулам (5), (6), (12), можно рассчитать по формуле (9) момент инерции I маятника и убедить­ся, что независимо от груза, I = const.

 

ПРАКТИЧЕСКАЯ ЧАСТЬ.

1. Наматывают на шкив нить с грузом Р₁ /массой m/ и отпускают груз, одновременно включая электрический секундомер. Замечают время t, в течение которого произойдет полное разматывание нити, фиксируя при этом перемещение груза h₁. После этого определяют перемещение h₂ груза вверх, при наматывании нити. Измерения проводят трижды, результаты вносят в таблицу I.

Таблица I. Масса груза m.

№	h1	h2	t
1.
2.
3.
ср.	=	=	=

 

2. Прикрепляют к грузу Р₁ груз такой же массы и повторяют измере­ния для груза Р₂ массой 2m. Результаты измерений вносят в таблицу 2

 

Таблица 2. Масса груза 2m.

№	h1	h2	t
1.
2.
3.
ср.	=	=	=

3. То же самое повторяют для груза Р₃ массой 3m. Результаты вносят в таблицу, аналогичную таблицам 1,2.

4. По средним значениям , , для каждого груза рассчитывают , , и .

5. Оценивают погрешности результатов. Ответ записывают в виде

,

.

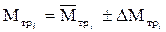6. Для окончательного вывода по итогам работы сделать сводную табли­цу и сравнить результаты.

груз	момент трения	момент инерции
Р1
Р2
Р3

 

 

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Какое движение называется вращательным?

2. Угловые и линейные характеристики при вращательном движении, их связь.

3. Понятие момента инерции абсолютно твердого тела. Единицы измерения.

4. Момент силы. Плечо силы. Единицы измерения.

5. Основной закон динамики вращательного движения.

6. Закон сохранения механической энергии.

7. Работа при вращательном движении.

8. Вывод расчетных формул (9) и (I2).

 

ЛИТЕРАТУРА.

1. Трофимова Т И. Курс физики, 1985г.

2. Яворский Б.М, Детлаф А. А. Справочник по физике. 1985г.

3. Савельев И В. Курс физики. т.I, 1989г.