Пусть даны плоскость и не лежащая на ней точка:
- перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости;
- конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра;
- расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость;
- наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости;
- конец отрезка, лежащий в плоскости, называется основанием наклонной;
- отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной.
На рисунке из точки А проведены к плоскости 
перпендикуляр АВ и наклонная АС. Точка В - основание перпендикуляра, точка С - основание наклонной, ВС - проекция наклонной АС на плоскость .
Теорема о трех перпендикулярах:
Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
Две пересекающиеся плоскости, называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.
Пример № 1
Через центр вписанной в треугольник окружности проведена прямая, перпендикулярная плоскости треугольника. Докажите, что каждая точка этой прямой равноудалена от сторон треугольника.
Решение:
Пусть А, В, С – точки касания сторон треугольника с окружностью, О – центр окружности и S – точка на перпендикуляре. Так как радиус ОА перпендикулярен стороне треугольника, то по теореме о трех перпендикулярах отрезок SА есть перпендикуляр к этой стороне, а его длина – расстояние от точки S до стороны треугольника. По теореме Пифагора SА= 
, где r – радиус вписанной окружности. Аналогично находим: 
, т.е. все расстояния от точки S до сторон треугольника равны.
Контрольные вопросы:
- Что такое перпендикуляр, опущенный из данной точки на плоскость?
- Что такое проекция наклонной?
Практическая часть:
1. Даны прямая а и плоскость . Проведите через прямую а плоскость, перпендикулярную плоскости .
2. Докажите, что если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости.
3. Из точки к плоскости проведены две наклонные, одна из которых на 20 см больше другой. Проекции наклонных равны 10 см и 30 см. Найдите наклонные.
4. Сторона квадрата равна 4 см. Точка, равноудаленная от всех вершин квадрата, находиться на расстоянии 6 см от точки пересечения его диагоналей. Найдите расстояние от этой точки до вершин квадрата.
5. Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найдите проекции наклонных.
6. Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2:3.
7. Прямая а перпендикулярна плоскости АВС, угол АСВ равен 90о, АС = 4, МD=3. Найти МС.
8. Прямая а перпендикулярна плоскости АВС. MD = 13. АС = 15, ВС = 20. АС 
ВС, МD АВ. Найти MC.
9. Катеты прямоугольного треугольника ABC (С =90°) равны 4 см и 3 см. Точка М находится на расстоянии √6 см от плоскости треугольника ABC и на одинаковом расстоянии от всех его вершин. Найти расстояние от точки М до вершин треугольника.
Литература:
1. Математика: учебник для учреждений нач. и сред. проф. образования / М.И. Башмаков. –М.: Издательский центр «Академия», 2010 г.
Самостоятельная работа № 5.
Решение задач на подсчет числа размещений, перестановок.
Цель занятия: освоить методы решения задач на расчет количества выборок
Теоретическая часть:
Комбинаторика — часть математики, которая посвящена решению задач выбора и расположения элементов некоторого конечного множества в соответствии с заданными правилами, т.е. комбинаторика решает задачи выбора элементов из конечного множества и размещения этих элементов в каком-либо порядке.
Размещениями из n – элементов по m – элементов (
) называются комбинации, составленные из данных n – элементов по m – элементов, которые отличаются друг от друга либо самими элементами либо порядком элементов.
=n(n-1)(n-2)…(n-m+1)
Пример № 1. Сколько трехзначных чисел можно составить из цифр от 1…9?
Решение:
= 
=504
Перестановками из n – элементов называется число размещений из этих n – элементов по n – элементов.
n(n-1)(n-2)…1=n!
Пример № 2. Сколькими способами можно расставить 5 книг на полке?
Решение:
=5!=120
Сочетаниями из n – элементов по m – элементов называются комбинации составленные из данных n – элементов по m – элементов, которые отличаются друг от друга хотя бы одним элементом.
Пример № 3. В группе 30 студентов. Для сдачи зачета их необходимо разбить на три группы. Сколькими способами это можно сделать?
n= 30
m=10
Контрольные вопросы:
1. Обозначьте цели комбинаторики.
2. Что называется числом сочетаний из n элементов по m?
3. Что называется числом размещений из n элементов по m?
4. Что называется перестановкой из n элементов?
Практическая часть:
1. Сколькими способами можно в группе из 25 человек направить 4 студента на научно – практическую конференцию?
2. Десять студентов обменялись рукопожатиями. Сколько было рукопожатий?
3. Сколькими способами можно составить трехцветный полосатый флаг из семи различных по цвету отрезов материи?
4. Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из пяти языков на любой из них?
5. Вычислите: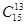 
6. Вычислите: 
7. Вычислите: 5! + 6!
8. Найдите число размещений из 10 элементов по 4.
9. Вычислите: 
10. Тридцать студентов обменялись фотокарточками. Сколько всего было фотокарточек?
11. Сколькими способами можно из восьми кандидатов можно выбрать три лица на три должности?
12. Решите уравнение: 
13. Вычислите значение выражения:
14. Вычислите значение выражения:
15. Сколькими способами можно составить список из десяти человек?
Литература:
1. Математика: учебник для учреждений нач. и сред. проф. образования / М.И. Башмаков. –М.: Издательский центр «Академия», 2010 г.
