Задание 4.1 Показанный на рисунке кривошипно-шатунный механизм описывается уравнением
 при i = 1, 2, 3,
при i = 1, 2, 3,
где  ,
,  ,
, 

Механизм должен удовлетворять следующим условиям:
| i | si | φi |
| 1,0 | 20o | |
| 1,2 | 45o | |
| 2,0 | 60o |
Cпроектировать устройство, отвечающее всем трем указанным выше условиям. Для этого записать трижды уравнение, описывающее работу механизма, и найти Ki. Определить значения а 1, а 2, а 3 соответствуют искомому решению.
Задание 4.2 При химической реакции:

процентное содержание X диссоциированного моля СO2 определяется уравнением
 ,
,
где Р – давление, выраженное в атмосферах, а К – константа равновесия, зависящая от температуры. Найти X при К = 1,648 (что соответствует 2800 К) и Р = 1 атм.
Раздел 5: Решение оптимизационных задач с помощью MATLAB
Задание 5.1 Спроектировать контейнер нового типа в форме кругового конуса без дна объемом 1 м3 (см. рисунок). Определить какие должны быть геометрические характеристики контейнера, чтобы его боковая поверхность была минимальной.

Задание 5.2 Предложено построить отель из цельнолитых бетонных комнат-модулей. В изготовленных прямоугольных модулях заранее делается электропроводка. Поскольку данное изделие предполагается выпускать серийно, очень важно обеспечить минимальную стоимость материалов. Требуется так проложить провода от настенного выключателя до места крепления светильника на потолке, чтобы их длина была минимальной. Дополнительное условие состоит в том, чтобы провода располагались либо в стене, либо в потолке. Выбрать вариант прокладки проводов в зависимости от величины у+ и определить необходимую для этого общую номинальную длину проводов.

Задание 5.3 Прямоугольный дорожный указатель размерами w и h изготовлен из металлического листа постоянной толщины. Площадь поля, содержащего изображение, должна составлять 1,5 м2. По нижней стороне указатель имеет поле 20 см, по трем остальным 10 см (см. рисунок) Определить значения w и h, при которых для изготовления указателя потребуется минимальное количество листового материала.

Задание 5.4 Расход жидкости при установившемся истечении через кольцевой зазор между двумя концентрическими трубками круглого сечения (жидкость несжимаемая, полностью развитое ламинарное течение) определяется формулой
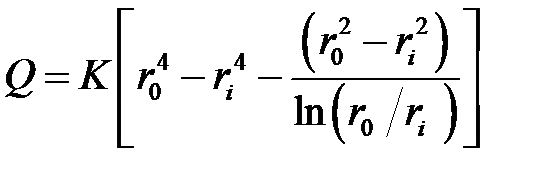 ,
,
где K – постоянная, зависящая от падения давления на единице длины, плотности и вязкости жидкости. Найти значения ri и r 0, при которых расход жидкости через поперечное сечение площадью 10 см2 максимален при дополнительном условии 2 см ≤ ri < r 0 ≤ 10 см.







