Раздел 3: Решение обыкновенных дифференциальных уравнений с помощью MATLAB

Задание 3.1 Материальная точка массой m закреплена на конце тонкого однородного стержня и может совершать свободные колебания (см. рисунок). Подготовить программу в MATLAB, которая моделировала бы движение этой системы, и выполнить расчет для полного цикла колебаний. При этом рекомендуется пользоваться следующим уравнением движения и дополнительными условиями:

,

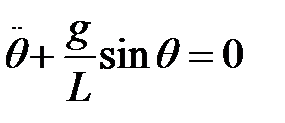
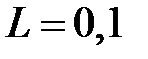м/с², м/с

Если угол отклонения θ мал, то дифференциальное уравнение можно линеари­зовать, приняв sin θ = θ. Сравнить полученные результаты с результатами для линейного случая.

Задание 3.2 Тело, показанное на рисунке, движется по плоской поверхности с трением, обусловливающим демпфирование колебаний. Его масса m = 4,5 кг, жесткость пружины k = 175 Н/м, коэффициент трения f = 0,3. Рассчитать движение тела в интервале времени с при начальных условиях:

см,

Результат представить графически.

Задание 3.3 С целью выяснить, нельзя ли усовершенствовать механизм, связывающий клавиши пианино с молоточками, было выполнено исследование этого механизма. Оледжски (Oledzki A., Dynamics of Piano Mechanisms, Mech. and Mach. Theory, No 7, 1972, pp. 373–­385) предложил следующую нелинейную модель:

,

.

В этих дифференциальных уравнениях х ₁ – смещение клавиши вниз, х ₂ – смещение молоточка вперед, F – направленная вниз сила, действующая на клавишу. Входящие в указанные уравнения постоянные имеют следующие значения:

m₁ = 0,0074 кг, a = 0,406 кг, b = 18,3 кг/м, k ₁ = 1,16∙10⁴ Н/м, k ₂ = 0,525∙10⁶ Н/м², k ₃ = 1,1∙10⁸ Н/м², 0 < F < 80 Н.

Подготовить программу в MATLAB, которая моделировала бы движение этой системы при F = 80 Н в интервале времени мс.

Задание 3.4 Систему отопления жилого помещения можно описать следующим дифференциальным уравнением:

,

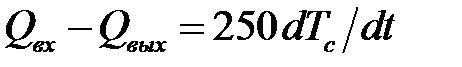где Q _вх – подвод тепла от нагревателя, Дж/с; Q _вых – потери тепла в окру­жающую среду, Дж/с; Т _с – температура во внутренних помещениях дома, ^oС; t – время, с.

Такие отопительные системы часто оборудуют термостатами, которые включают и выключают нагреватель в зависимости от величины разности за­данной температуры Т_d и действительной температуры в помещении Т _с.

Пусть суточные потери тепла при температуре окружающей среды 0 °С составляют , а регулятор работает в соответствии с графиком

Написать программу для моделирования отопительной системы при Т_d = 22 °С, предполагая, что начальная температура в помещении Т_c.

Задание 3.5 Дифференциальное уравнение изгибной линии бруска с постоянным поперечным сечением имеет вид

.

при начальных условиях , и м, .

Составить программу в MATLAB для расчета изгибной линии бруска y (x), пользуясь:

а) точным выражением для кривизны

б) приближенным выражением для кривизны

Сравнить полученные результаты.