Мы приведем два способа решения системы линейных дифференциальных уравнений с постоянными коэффициентами. Первый способ называют методом исключения неизвестной функции. Второй способ основан на использовании собственных чисел и собственных векторов матрицы.
а) Сначала на примере продемонстрируем метод исключения неизвестной функции (и её производной), при этом система сводится к одному уравнению второго порядка с одной неизвестной функцией.
Задача 14. Найти общее решение системы линейных дифференциальных уравнений: 
Решение. Продифференцируем второе уравнение этой системы:

Составляем новую систему дифференциальных уравнений:

Исключив  из последней системы, получим линейное однородное уравнение с постоянными коэффициентами
из последней системы, получим линейное однородное уравнение с постоянными коэффициентами
 .
.
Соответствующее характеристическое уравнение  имеет комплексные корни:
имеет комплексные корни: 
Следовательно,  где
где  и
и
 - произвольные постоянные. Из последнего уравнения исходной системы
- произвольные постоянные. Из последнего уравнения исходной системы 



Итак, общее решение системы:

B) Решить систему линейных дифференциальных уравнений с постоянными коэффициентами

можно и методами линейной алгебры, используя характеристическое уравнение.
Найдем корни характеристического уравнения
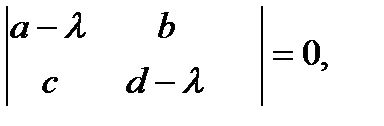 или
или 
Мы рассмотрим только случай, когда характеристическое уравнение имеет различные действительные корни  и
и  В этом случае каждому корню соответствует некоторый собственный вектор. Так, корню
В этом случае каждому корню соответствует некоторый собственный вектор. Так, корню  соответствует вектор
соответствует вектор 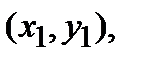 найденный из системы уравнений
найденный из системы уравнений
 или
или 
а корню  соответствует вектор
соответствует вектор  определяемый системой
определяемый системой
 или
или 
Зная векторы 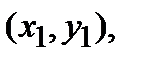 и
и  легко выписывается общее решение системы
легко выписывается общее решение системы

Задача 15. Найти общее решение системы линейных дифференциальных уравнений:

Решение. Составим и решим характеристическое уравнение
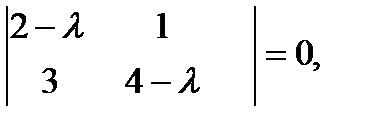 или
или 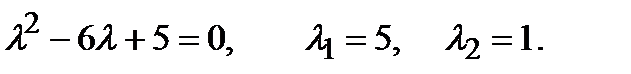
Найдем собственный вектор, соответствующий собственному значению 
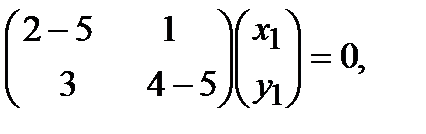 или
или 
Положим для определенности 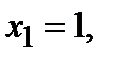 тогда
тогда  Итак, собственному значению
Итак, собственному значению  соответствует собственный вектор(1,3). Аналогично для
соответствует собственный вектор(1,3). Аналогично для 
 или
или 
Положим для определенности  тогда
тогда 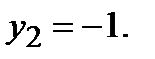 Итак, собственному значению
Итак, собственному значению  соответствует собственный вектор (1,-1).
соответствует собственный вектор (1,-1).
Выписываем теперь общее решение системы:
 Окончательно:
Окончательно: 
Задание для самостоятельной работы
Найти общее решение системы линейных дифференциальных уравнений (систему под номером а.) решать методом исключения неизвестной функции; систему под номером b.) решать c помощью характеристического уравнения):
| a) | 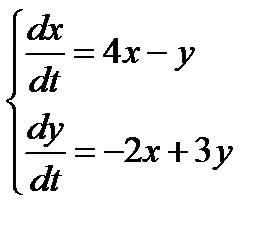
| b) | 
|
Ответы к заданию:
| a) | 
| b) | 
|
РЯДЫ
Числовые ряды
Не останавливаясь на основных определениях теории рядов [1. Гл. XI, §1], приведем только их признаки сходимости:
а) интегральный признак Коши сходимости ряда 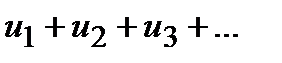 с положительными членами. Если
с положительными членами. Если  , где
, где  - убывающая непрерывная функция, то ряд и интеграл
- убывающая непрерывная функция, то ряд и интеграл  сходятся или расходятся одновременно (
сходятся или расходятся одновременно ( -некоторое число,
-некоторое число,  );
);
б) признак Даламбера. Пусть  (начиная с некоторого члена ряда) и существует предел
(начиная с некоторого члена ряда) и существует предел
 .
.
Тогда ряд  сходится, если
сходится, если  , и расходится, если
, и расходится, если  . Если
. Если  , вопрос о сходимости ряда остается открытым;
, вопрос о сходимости ряда остается открытым;
в) признак Коши. Пусть  (начиная с некоторого члена ряда) и существует предел
(начиная с некоторого члена ряда) и существует предел
 .
.
Тогда ряд 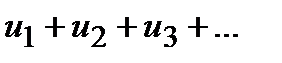 сходится, если
сходится, если  , и расходится, если
, и расходится, если  . В случае, когда
. В случае, когда  , вопрос о сходимости ряда остается открытым;
, вопрос о сходимости ряда остается открытым;
г) первый признак сравнения. Если  (начиная с некоторого
(начиная с некоторого 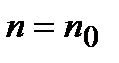 ), то из сходимости ряда
), то из сходимости ряда 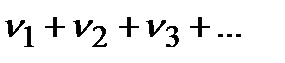 следует сходимость ряда
следует сходимость ряда 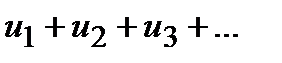 , а из расходимости ряда
, а из расходимости ряда 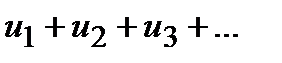 следует расходимость ряда
следует расходимость ряда  ;
;
д) второй признак сравнения. Если существует конечный и отличный от нуля предел
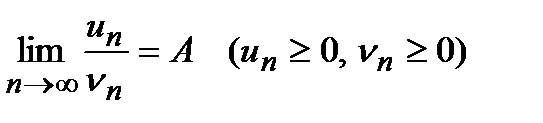 ,
,
то ряды 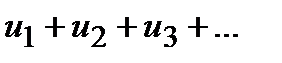 и
и  сходятся или расходятся одновременно;
сходятся или расходятся одновременно;
е) признак Лейбница. Ряд с чередующимися знаками  сходится, если
сходится, если 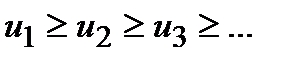 и
и 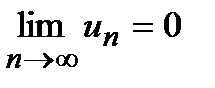 .
.
Отметим еще необходимое условие сходимости ряда: Для того, чтобы ряд 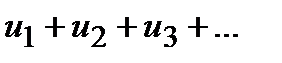 сходился, необходимо, чтобы
сходился, необходимо, чтобы 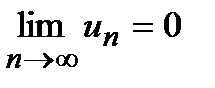 .
.
Задача 1. Исследовать сходимость числового ряда  .
.
Решение. Применим интегральный признак. Ясно, что функция  будет непрерывной при
будет непрерывной при  и убывающей, при этом
и убывающей, при этом 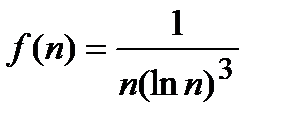 .
.
Рассмотрим интеграл
 .
.
Так как этот интеграл сходится, то сходится и ряд.
Задача 2. Исследовать сходимость числового ряда  .
.
Решение. Применим признак Даламбера. Очевидно, что
 ,
,  ,
,
тогда 
т.к  , то ряд сходится.
, то ряд сходится.
Задача 3. Исследовать сходимость числового ряда  .
.
Решение. Для решения вопроса о сходимости этого ряда используем признак Коши
 ,
,
т.к.  , то ряд сходится.
, то ряд сходится.
Задача 4. Исследовать сходимость числового ряда  .
.
Решение. Воспользуемся признаком Даламбера. 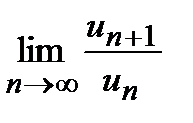 =
=  =
=  =
= 
т.к.  , то ряд расходится.
, то ряд расходится.
Этот же вывод можно сделать, исследуя общий член этого ряда  c помощью правила Лопиталя легко выяснить, что он не стремится к нулю при
c помощью правила Лопиталя легко выяснить, что он не стремится к нулю при  , т.е. не выполняется необходимое условие сходимости ряда;
, т.е. не выполняется необходимое условие сходимости ряда;
Задача 5. Исследовать сходимость числового ряда  .
.
Решение. Легко видеть, что для этого ряда  , т.е. признак Даламбера не дает ответа на вопрос о его сходимости. Воспользуемся первым признаком сравнения. Так как
, т.е. признак Даламбера не дает ответа на вопрос о его сходимости. Воспользуемся первым признаком сравнения. Так как

и ряд  сходится (см. сходимость обобщенного гармонического ряда
сходится (см. сходимость обобщенного гармонического ряда  ), то и наш ряд сходится.
), то и наш ряд сходится.
Можно было бы воспользоваться вторым признаком сравнения. Сравним наш ряд с тем же рядом  . Так как
. Так как 
 =
=  =1
=1
то из сходимости ряда  следует сходимость нашего ряда;
следует сходимость нашего ряда;
Задача 6. Исследовать сходимость числового ряда  .
.
Решение. Очевидно, что члены этого ряда удовлетворяют всем условиям признака Лейбница. То есть, ряд сходится.
Задача 7. Исследовать сходимость числового ряда  .
.
Решение. Общий член этого ряда  и, значит, не стремится к нулю. Следовательно, ряд расходится.
и, значит, не стремится к нулю. Следовательно, ряд расходится.
Задание для самостоятельной работы
Исследовать сходимость числовых рядов:
a)  ; b)
; b) 
c)  d)
d) 
Ответы к заданию:
| а) | Ряд расходится (использовать необходимый признак сходимости). | b) | Ряд расходится (использовать признак сравнения). |
| c) | Ряд расходится (использовать интегральный признак сходимости). | d) | Ряд сходится (использовать признак Даламбера). |
Функциональные ряды
(См. (1), гл. ХΙ, §§ 2 – 5 и гл. ХΙΙ, §1).
Задача 8. Найти интервал сходимости степенного ряда

Решение. Пусть дан степенной ряд  . Число
. Число  есть радиус сходимости степенного ряда, если при
есть радиус сходимости степенного ряда, если при  ряд сходится, а при
ряд сходится, а при  - расходится. Интервалом сходимости называют интервал
- расходится. Интервалом сходимости называют интервал  . Известно, что радиус сходимости степенного ряда вычисляется по формуле
. Известно, что радиус сходимости степенного ряда вычисляется по формуле 
Воспользовавшись этой формулой, вычислим радиус сходимости нашего степенного ряда
 и
и 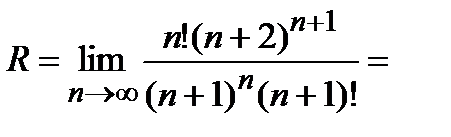



Итак, радиус сходимости  Следовательно, интервалом сходимости нашего ряда будет
Следовательно, интервалом сходимости нашего ряда будет 
Задание для самостоятельной работы
Найти интервал сходимости степенных рядов:
| a) | 
| b) | 
|
Ответы к заданию:
| a) | 
| b) | 
|
Задача 9. Разложить функцию  в ряд Фурье в указанных интервалах
в ряд Фурье в указанных интервалах

Решение. Если функция  удовлетворяет условиям теоремы Дирихле в некотором интервале
удовлетворяет условиям теоремы Дирихле в некотором интервале  , то в точках непрерывности функции, принадлежащих этому интервалу, справедливо разложение
, то в точках непрерывности функции, принадлежащих этому интервалу, справедливо разложение

где 
В нашем случае 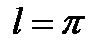 и
и  = 0 при
= 0 при  , поэтому
, поэтому
 .
.
Аналогично

Итак, искомый ряд Фурье можно записать в следующем виде:

Задание для самостоятельной работы
Разложить функцию  в ряд Фурье в указанных интервалах
в ряд Фурье в указанных интервалах

Указание. Функция нечетна, поэтому все аn=0. Вычислять bn следует по формуле, приведенной выше.

Задача 10. Вычислить определенный интеграл
 с точностью до 0,001.
с точностью до 0,001.
Для этого подынтегральную функцию следует разложить в ряд, который затем почленно проинтегрировать.
Решение. Разлагая функцию 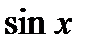 по степеням x, получим:
по степеням x, получим:



Так как шестой член меньше 0,001, то ограничимся пятью членами. Ошибка по модулю, согласно теореме Лейбница, не превышает первого из отбрасываемых членов (в нашем случае ряд знакопеременный с убывающими членами). Получаем 
Задание для самостоятельной работы
Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию следует разложить в ряд, который затем почленно проинтегрировать:
| a) | 
| Ответ: 0,747, |
| b) | 
| Ответ: 0,494. |
Контрольная работа на тему:
«Дифференциальные уравнения»
Задание 1. Найти общее решение дифференциальных уравнений.
| 1. | а)  ; ;
| б)  . .
|
| 2. | а) 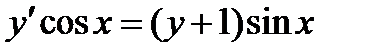 ; ;
| б)  . .
|
| 3. | а)  ; ;
| б)  . .
|
| 4. | а)  ; ;
| б)  . .
|
| 5. | а)  ; ;
| б)  . .
|
| 6. | а)  ; ;
| б)  . .
|
| 7. | а) 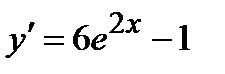 ; ;
| б)  . .
|
| 8. | а)  ; ;
| б)  . .
|
| 9. | а)  ; ;
| б)  . .
|
| 10. | а) 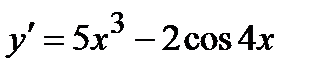 ; ;
| б)  . .
|
Задание 2. Найти общее решение дифференциального уравнения.
1. 
| 2. 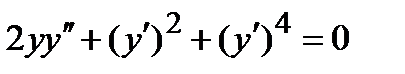
|
3. 
| 4. 
|
5. 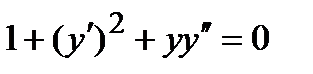
| 6. 
|
7. 
| 8. 
|
9. 
| 10. 
|
Задание 3. Найти частное решение дифференциального уравнения  , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 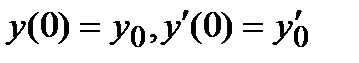 .
.
1. 
2. 
3. 
4. 
5. 
6. 
7. 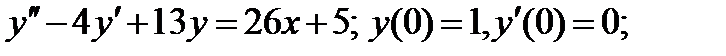
8. 
9. 
10. 
Задание 4. Найти решение системы линейных дифференциальных уравнений с постоянными коэффициентами.
| 1. | 
| 2. | 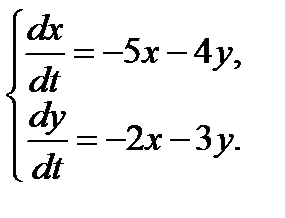
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
Контрольная работа на тему: «Ряды»
Задание 1. Исследовать сходимость числового ряда.
| 1. | 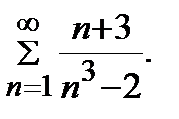
| 2. | 
|
| 3. | 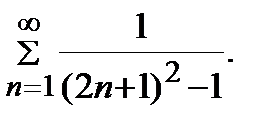
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 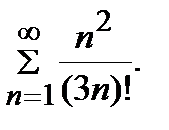
|
| 9. | 
| 10. | 
|
Задание 2. Найти интервал сходимости степенного ряда и исследовать на сходимость на концах интервала.
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 
| 8. | 
|
| 9. | 
| 10. | 
|
Задание 3. Вычислить определенный интеграл  с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.
с точностью до 0,001, разложив подынтегральную функцию в ряд и затем проинтегрировав его почленно.
| 1. | 
| 2. | 
|
| 3. | 
| 4. | 
|
| 5. | 
| 6. | 
|
| 7. | 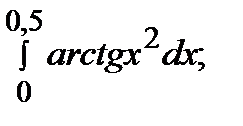
| 8. | 
|
| 9. | 
| 10. | 
|
Задание 4. Разложить данную функцию  в ряд Фурье в интервале
в ряд Фурье в интервале  .
.
1.  , ,  ; ;
| 2.  , ,  ; ;
|
3.  , ,  ; ;
| 4.  ; ;
|
5.  ; ;
| 6.  ; ;
|
7.  ; ;
| 8.  ; ;
|
9.  , , 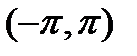 ; ;
| 10.  , ,  . .
|
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пискунов Н.С. Дифференциальное и интегральное исчисления.Т.2.-M.: Интеграл-Пресс, 2004.- 560 с.
2. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов -СПб.: Изд ─ во “Лань”, 2003. – 736c.






