Для решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами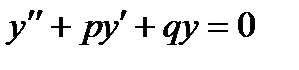 
составляется соответствующее характеристическое уравнение: 
.
- Если корни 
и 
характеристического уравнения действительны и различны, то общее решение однородного уравнения будет иметь вид:
.
- Если 
и 
действительны и равны между собой, т.е. 
, то общее решение запишется в виде 
.
- Если корни являются комплексными числами 
, 
, то общее решение представляется в виде
.
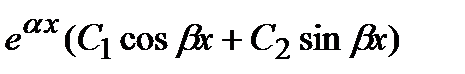Задача 8. Найти общие решения уравнений:
| a) | 
|
| b) | 
|
| c) | 
|
Решение.
а) Составим соответствующее характеристическое уравнение и решим его: 
, 
Согласно сказанному выше, общее решение можно записать в виде 
.
b) Составляем характеристическое уравнение 
, 
.Отсюда 
.
c) Характеристическое уравнение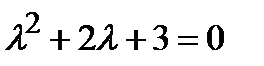 
имеет решение 
.
Следовательно, 
Задание для самостоятельной работы
Найти общее решение дифференциальных уравнений:
a)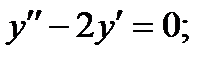 
|
b) 
|
c) 
|
Ответы к заданию:
a) 
|
b) 
|
c) 
|
Линейные неоднородные дифференциальные уравнения второго порядка с постоянными
Коэффициентами
Общее решение линейного неоднородного дифференциального уравнения 
можно записать в виде 
где 
- общее решение соответствующего однородного дифференциального уравнения, а Y - частное решение данного неоднородного уравнения.
Функция Y может быть найдена методом неопределенных коэффициентов в следующих простейших случаях:
1) 
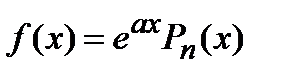, где 
многочлен степени 
.
Если 
не является корнем характеристического уравнения, то частное решение ищут в виде 
, где 
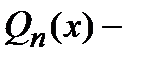многочлен степени с неизвестными коэффициентами.
Если 
- корень характеристического уравнения кратности
, то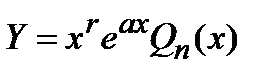 
.
2) 
Если 
не является корнем характеристического уравнения, то полагают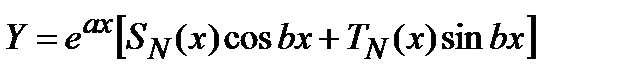 
,
где 
многочлены степени 
.
Если 
корни характеристического уравнения кратности 
(для уравнений второго порядка 
), то полагают 
.
Функцию, находящуюся в правой части линейного неоднородного дифференциального уравнения с постоянными коэффициентами, имеющую вид 
принято называть специальной правой частью.
Задача 9. Найти общее решение уравнения
.
Решение. Найдем общее решение 
однородного дифференциального уравнения 
. Характеристическое уравнение 
имеет корни 
. Следовательно, 
.
Правая часть уравнения равна 
. Следовательно, 
, и поскольку 
не является корнем характеристического уравнения, то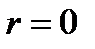 
. Поэтому частное решение ищем в виде 
.
Дифференцируя Y два раза и подставляя производные в данное уравнение, получим
Сокращая на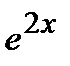 
и приравнивая коэффициенты при одинаковых степенях 
левой и правой частей последнего равенства, находим:
Отсюда 
. Значит, общее решение данного уравнения имеет вид
.
Задача 10. Найти общее решение уравнения 
.
Решениe. Найдем общее решение 
однородного дифференциального уравнения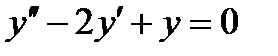 
.
Характеристическое уравнение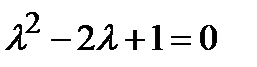 
имеет корни 
(кратность корня 
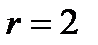). Следовательно, 
.
Правая часть уравнения имеет вид 
. Тогда 
. Так как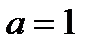 
совпадает с корнем 
кратности 
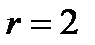, то частное решение ищем в виде 
.
Дифференцируя Y два раза, подставляя в уравнение и приравнивая коэффициенты, получим: 
.
Общее решение данного уравнения имеет вид
Задача 11. Найти частное решение дифференциального уравнения 
, удовлетворяющее начальным условиям 
.
Решение. Найдем общее решение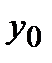 
однородного дифференциального уравнения: 
.
Составим характеристическое уравнение 
, его корни 
Тогда общее решение однородного уравнения будет иметь вид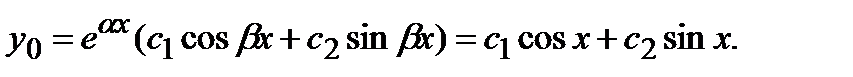 
Правая часть неоднородного дифференциального уравнения в общем виде имеет вид: 
.
Правая часть данного уравнения, т.е. 
получается при а=0, b=1, что соответствует числу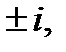 
которое является корнем характеристического уравнения кратности один (
), поэтому частное решение уравнения нужно искать в виде 
.
Дифференцируя это выражение два раза и подставляя в данное уравнение найденные значения 
приравниваем коэффициенты в обеих частях равенства при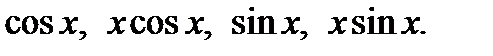 
В результате получаем систему уравнений:
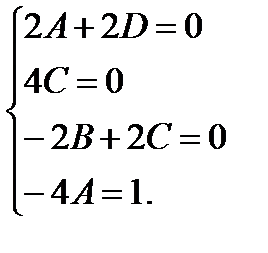
Решив эту систему уравнений, получим 
. Следовательно, 
.
Итак, общее решение неоднородного уравнения будет иметь вид 
.
Чтобы учесть начальные условия, найдем 
:
Учитывая, что при 
выполняются равенства 
и 
, находим 
.
Таким образом, искомое частное решение исходного уравнения, удовлетворяющее начальным условиям, имеет вид: 
.
Для решения линейных неоднородных дифференциальных уравнений можно использовать также метод вариации произвольных постоянных (метод Лагранжа).
Если 
и 
линейно независимые частные решения уравнения 
, то решение неоднородного уравнения 
находится в виде: 
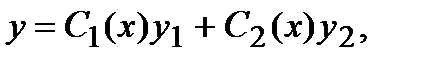где 
и 
функции от 
, удовлетворяющие системе уравнений:
Задача 12. Найти решение дифференциального уравнения: 
.
Решение. Решим сначала однородное уравнение 
, для чего составим характеристическое уравнение 
. Ясно, что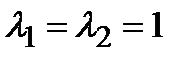 
. Итак, получим общее решение однородного уравнения 
. Отсюда, 
Будем теперь искать общее решение нашего неоднородного уравнения в виде 
, где 
, и 
- функции, удовлетворяющие указанной выше системе линейных уравнений.
Составим и решим эту систему с учетом наших данных:
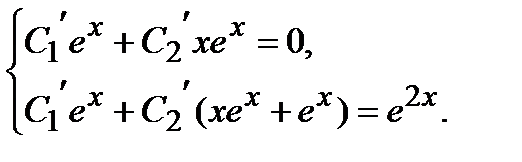
где А – произвольная константа.
Подставляя значение 
в первое уравнение последней системы, получим
.
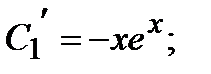
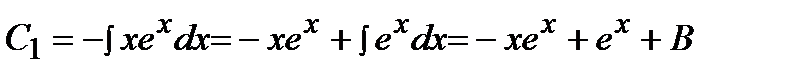Итак, общее решение нашего уравнения
Задание для самостоятельной работы
Найти общее решение дифференциальных уравнений методом вариации произвольных постоянных:
a) 
|
b)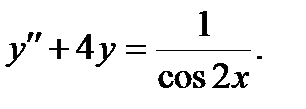 
|
Ответы к заданию:
a)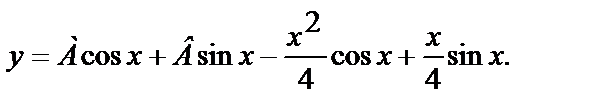 
Указания. Общее решение однородного уравнения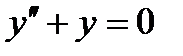 
Поэтому 
Решение неоднородного уравнения следует искать в виде
где 
, и 
- функции, удовлетворяющие системе уравнений
Решать эту систему лучше, пользуясь правилом Крамера.
b) 
Задача 13. Найти частное решение дифференциального уравнения 
, удовлетворяющее указанным начальным условиям: 
.
Решение. Прежде чем решать эту задачу, необходимо очень тщательно изучить решение задачи 12.
Найдем сначала общее решение нашего уравнения.
Соответствующее однородное уравнение 
, а его характеристическое уравнение 
. Имеем
, 
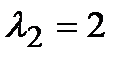. Общее решение однородного уравнения
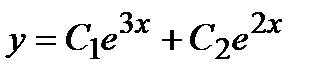. Поэтому общее решение неоднородного уравнения будем искать в виде 
, где 
и 
удовлетворяют следующей системе уравнений:
Подставляя значение 
в первое уравнение системы, получим 
.
Следовательно, 
, 
Итак, общее решение неоднородного уравнения имеет вид
.
Найдем теперь частное решение, удовлетворяющее указанным начальным условиям, подобрав соответствующие константы А и В:
;
.
По условию
Отсюда следует, что искомое частное решение имеет вид
.
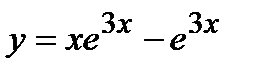