ПРАКТИЧЕСКАЯ РАБОТА 4
РАСЧЕТ ПОКАЗАТЕЛЕЙ ДИФФЕРЕНЦИАЦИИ
Цель работы: оценить степень неравномерности распределения признака.
Порядок выполнения работы:
1. Рассчитать коэффициент фондовой дифференциации по первичным данным.
2. Охарактеризовать дифференциацию признака сгруппированных данных.
3. Интерпретировать полученные результаты.
Анализ вариации, проведенный в практической работе № 3, целесообразно дополнить показателями дифференциации. Для этого может быть рассчитан так называемый коэффициент фондовой дифференциации 
, который представляет собой соотношение двух средних, полученных из 10% наибольших и наименьших значений признака:
Таким образом, показывает, во сколько раз размер признака у 10% совокупности с наивысшими показателями превышает размер признака 10 % совокупности с наименьшими показателями.
Следует помнить, что рассчитывать коэффициенты дифференциации при малом объеме совокупности нецелесообразно.
Если анализируются сгруппированные данные, то для характеристики дифференциации можно воспользоваться соотношением десятой и первой децили (децили делят все число единиц в совокупности на 10 равных частей). Для определения децилей может использоваться следующая формула:
,
где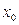 
- нижняя граница интервала, в котором находится дециль;
- сумма накопленных частот интервалов, предшествующих интервалу, в котором находится дециль;
- частота интервала, в котором находится дециль.
Расчет их ведется по общей схеме:
1. определяется номер для первой децили и для девятой децили:
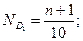
устанавливается интервал, где должны будут находиться децили;
2. рассчитывается значение децилей при предположении равномерного наращивания величины интервала на каждую единицу частоты (частости);
3. определяется коэффициент децильной дифференциации:
Покажем расчет перечисленных коэффициентов на следующих примерах.
Пример 1.
Рассмотрим ряд распределения по первичным данным о размере прибыли 30 банков региона за год, млн. руб.
5,2 6,4 8,7 5,1 3,7 4,3 9,2 6,6 4,6 8,1 5,7 6,1 6,8 6,9 5,0
8,3 8,4 7,2 7,9 6,5 7,9 6,0 9,1 7,3 7,0 7,9 4,9 7,6 8,0 5,9.
Определяем, что 3 банка (10 % от общего числа) с наименьшим размером прибыли 3,7 млн.; 4,3 млн. и 4,6 млн. руб. имеют 
= 4,2 млн. руб.
Для трех банков с наибольшими значениями 8,4 млн., 9,1 млн. руб. и 9,2 млн. руб. средняя арифметическая 
составляет 8,9 млн. руб.
Следовательно, коэффициент фондовой дифференциации будет равен:
Это означает, что размер прибыли у 10% банков с наивысшими доходами более чем в 2 раза превышает размер прибыли 10% банков с наименьшими доходами.
Пример 2.
Расчет коэффициента децильной дифференциации проведем на основе данных о распределении населения России по размеру среднедушевого денежного дохода в 2005 г.
Таблица 8
Распределение населения Российской Федерации по размеру среднедушевого дохода
Определим номера первой и девятой децилей:
По имеющимся данным первая дециль будет находиться во втором интервале – 1500 - 2500 руб., а девятая – в интервале свыше 12000 руб. Их значения соответственно составят:
руб.
руб.
Далее, коэффициент децильной дифференциации равен:
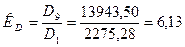
Таким образом, наименьший уровень среднедушевого денежного дохода 10% наиболее обеспеченного населения и наивысший уровень среднедушевого денежного дохода 10% наименее обеспеченного населения различались более чем в 6 раз.
