ОТЧЕТ
По лабораторной работе №7
по курсу Теория оптимального управления
Метод динамического программирования для дискретной задачи оптимального управления
ОГУ 010200.6006.02 О
Руководитель
_____________ Иванова Ю.П.
“___ ”______________2011 г.
Исполнитель
студент гр. 08 ПриМ
_______________Кияева Е. А.
“___ ” _____________2011 г.
Оренбург 2011
Содержание
Постановка задачи………………………………………………………..3
Алгоритм реализации схемы Беллмана….…………….………….……7
Практическая часть……………………………………………………….8
Приложение А – Код программы…….……………………………….11
Постановка задачи
Рассмотрим модель очистки воды от загрязнения органическими отходами.
Задача оптимального управления с ограничениями на управление:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
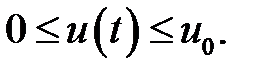 (6)
(6)
Здесь 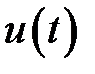 (мг. /ед.врем. л) – количество отходов, удаленных из единицы объема в единицу времени;
(мг. /ед.врем. л) – количество отходов, удаленных из единицы объема в единицу времени;
 (мг. /л) – концентрация органических отходов в момент времени t;
(мг. /л) – концентрация органических отходов в момент времени t;
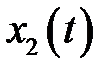 (мг. /л.) – дефицит кислорода в воде в момент времени t;
(мг. /л.) – дефицит кислорода в воде в момент времени t;
а (ед.врем.) – коэффициент, характеризующий стоимость работ в единицу времени;
 (1/ ед.врем.) – коэффициент отбора кислорода за единицу времени;
(1/ ед.врем.) – коэффициент отбора кислорода за единицу времени;
 (1/ед.врем.) – коэффициент реаэрации в единицу времени;
(1/ед.врем.) – коэффициент реаэрации в единицу времени;
 – начальное значение в момент
– начальное значение в момент 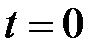 дефицита кислорода и концентрации отходов соответственно;
дефицита кислорода и концентрации отходов соответственно;
В уравнении (2) производная  (мг. /ед.врем. л) характеризует скорость разложения отходов в единицу времени.
(мг. /ед.врем. л) характеризует скорость разложения отходов в единицу времени.
В уравнении (3)  (мг. /ед.врем. л) характеризует динамику дефицита кислорода в единицу времени.
(мг. /ед.врем. л) характеризует динамику дефицита кислорода в единицу времени.
В неравенстве  (мг. /ед.врем. л)
(мг. /ед.врем. л)  – максимальное количество отходов, удаленных из единицы объема в единицу времени.
– максимальное количество отходов, удаленных из единицы объема в единицу времени.
Целью управления является минимизация суммарных затрат на проведение очистных работ, уменьшение концентрации отходов и дефицита кислорода в течении рассматриваемого периода времени Т.
Провести эксперимент при следующих значениях параметров и программно реализовать его:

Применим для решения задачи (1) – (6) схему Беллмана. Для определенности будем считать, что в задаче  и заданы параллельные фазовые ограничения.
и заданы параллельные фазовые ограничения.
Алгоритм реализации схемы Беллмана
| Шаг | Действие |
Задать разбиения:
а) отрезка времени  : :  б)
б)  – ограничения по – ограничения по 
 в)
в)  – ограничения по – ограничения по 
 г)
г) 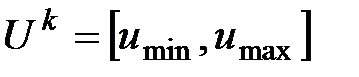 – ограничения по u – ограничения по u
 ; ;
| |
| Первый этап (по убывающему индексу) | |
Вычислить значения функции Беллмана в точках терминального множества 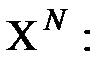
 ,
где ,
где 
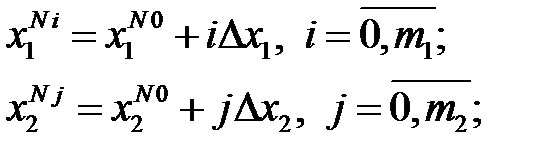
| |
Начало цикла по 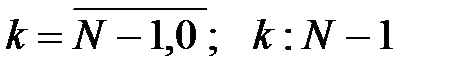 ; ;
| |
Положить 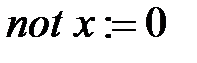 – число проколотых точек.
(Точка называется проколотой, если она не принадлежит множеству достижимости)
Организовать цикл по точкам множества – число проколотых точек.
(Точка называется проколотой, если она не принадлежит множеству достижимости)
Организовать цикл по точкам множества  ; ;
| |
Вычислить координаты точки 

| |
Положить 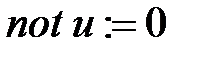 – число недопустимых управлений в точке – число недопустимых управлений в точке 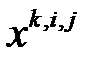 ; ;
| |
Организовать цикл по допустимым управлениям 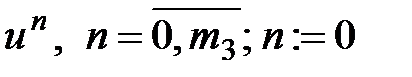 ; ;
| |
Вычислить управления  ; ;
| |
Вычислить точку 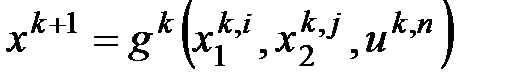 ; ;
| |
Проверить выполнение фазового ограничения (принадлежит ли точка  множеству множеству  ): ):

| |
Найти ближайшую к  непроколотую точку непроколотую точку  сетки сетки  ; если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше чем ; если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше чем  ) являются проколотыми, то ) являются проколотыми, то  и переход к шагу 14; и переход к шагу 14;
| |
Вычислить  ; ;
| |
Найти  ; ;
| |
Положить  ; ;
| |
Перейти к следующему шагу цикла по n, т.е. положить 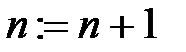 и проверить условие окончания цикла: и проверить условие окончания цикла:  ; ;
| |
Проверяем, не является ли точка  проколотой: проколотой:
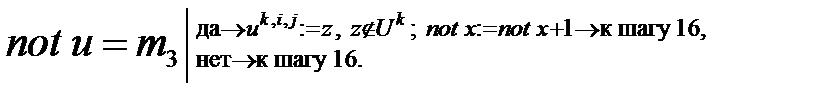
| |
Перейти к следующей итерации цикла по i,j, т.е.
а) положить 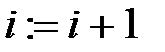 и проверить условие и проверить условие
 б) положить
б) положить  и проверить условие и проверить условие

| |
Проверить, все ли точки  сетки сетки  являются непроколотыми: являются непроколотыми:

| |
Перейти к следующей итерации цикла по  , т.е. полагаем , т.е. полагаем 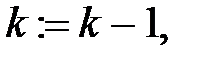 и проверить условие окончания цикла: и проверить условие окончания цикла:

| |
Получить функцию Беллмана  и и 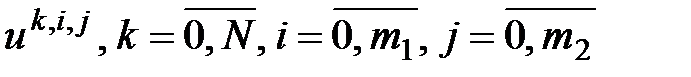 − синтез управления; − синтез управления;
| |
| Второй этап | |
Найти ближайшую к  непроколотую точку непроколотую точку  сетки сетки  . Если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше, чем . Если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше, чем 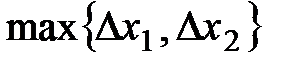 ) являются проколотыми, то “нет решений” и идти к шагу 32, иначе − к шагу 21; ) являются проколотыми, то “нет решений” и идти к шагу 32, иначе − к шагу 21;
| |
Вычислить 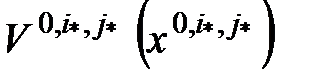 ; ;
| |
| Третий этап (по возрастающему индексу) Определение оптимальной траектории и программного управления | |
Положить  ; ;
| |
Организовать цикл по  полагаем полагаем  ; ;
| |
Найти ближайшую к  непроколотую точку непроколотую точку  сетки сетки  . Если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше, чем . Если все ближайшие точки сетки (т.е. точки, находящиеся на расстоянии меньше, чем  ) являются проколотыми, то “нет решений” и надо перейти к шагу 32, иначе − к шагу 25; ) являются проколотыми, то “нет решений” и надо перейти к шагу 32, иначе − к шагу 25;
| |
Определить соответствующее ей управление – синтез и полагаем  ; ;
| |
Вычислить точку  ; ;
| |
Перейти к следующему шагу цикла по  , т.е. положить , т.е. положить  и проверить условие и проверить условие 
| |
| Получить приближение оптимальной траектории и программного управления, вычислить искомое значение функционала I; | |
Проверить точность полученного решения:

| |
Для получения более точного решения увеличиваем число точек разбиения  множеств множеств 
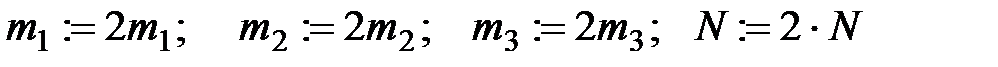 .
Перейти к шагу 0; .
Перейти к шагу 0;
| |
 − решение задачи. Конец алгоритма. − решение задачи. Конец алгоритма.
|
Практическая часть
1) Дискретная аппроксимация.
Разобьем отрезок [0,T] на N частей точками  и,приняв их в качестве узловых, интеграл (1) заменим квадратурной формулой прямоугольников. Дифференциальные уравнения (2), (3) - разностным уравнением с помощью схемы Эйлера. В результате придем к дискретной задаче оптимального управления вида:
и,приняв их в качестве узловых, интеграл (1) заменим квадратурной формулой прямоугольников. Дифференциальные уравнения (2), (3) - разностным уравнением с помощью схемы Эйлера. В результате придем к дискретной задаче оптимального управления вида:

2) Результаты выполнения программы




Концентрация органических отходов и дефицит кислорода в воде с течением времени уменьшаются. Количество отходов, удаленных из единицы объема в единицу времени, остается постоянным.
Таким образом, при увеличении продолжительности очистки воды количество отходов и дефицит кислорода в воде будут уменьшаться.
Приложение А
(обязательное)
Код программы
#pragma package(smart_init)
#pragma resource "*.dfm"
TForm1 *Form1;
struct point
{bool f;double x; double y;};
double dt, dx1,dx2,du,eps,J,J_,k1=0.0004321,k2=0.008281,a,T;
int N,m1,m2,m3;
typedef double **massiv;
typedef double *masv;
struct sov
{massiv u,V;};
typedef sov *m;
double Bk(double x, double y, double u)
{
return (a*u+x+y)*dt;
}
double f(double x1,double x2, double u,int i)
{
switch (i)
{
case 0: return x1-(k1*x1+u)*dt;
case 1: return x2+(k1*x1-k2*x2)*dt;
}
}
double I(massiv x, masv u)
{
double s=0;
for (int i=0;i<N;i++)
s+=(a*u[i]+x[0][i]+x[1][i])*dt;
return s;
}
bool D(point x)
{
if ((x.x>=1)&&(x.x<=10))
if ((x.y>=-10)&&(x.y<=10)) return true;
else return false;
else return false;
}
int round (double a)
{
if (a-int (a)>0.5) return int(a)+1;
if (a-int(a)<=0.5) return int (a);
}
point prok(point x)
{
point a;
double d;
if (dx1>dx2) d=dx1;
else d=dx2;
a.f=false;
int i0,j0;
a.x=round((x.x-1)/dx1);
a.y=round((x.y+10)/dx2);
if ((1+a.x*dx1>=1)&&(1+a.x*dx1<=10)&&(-10+a.y*dx2>=-10)&&(-10+a.y*dx2<=10)) a.f=true;
else
if (((x.x+d>=1)&&(x.x<1))||((x.x-d>10)&&(x.x>10))||((x.y+d>=-10)&&(x.y<-10))||((x.y-d<=10)&&(x.y>10)))
{
a.f=true;
if (x.x<1) a.x=0;
if (x.x>10) a.x=m1;
if (x.y<-10) a.y=0;
if (x.y>10) a.y=m2;
}
return a;
}
double max(double a, double b)
{
if (a>b) return a;
else return b;
}
//---------------------------------------------------------------------------
void __fastcall TForm1::Button1Click(TObject *Sender)
{
int i0,j0,i_0,j_0;
eps=StrToFloat(Edit6->Text);
N=StrToInt(Edit4->Text);
m1=StrToInt(Edit1->Text);
m2=StrToInt(Edit2->Text);
m3=StrToInt(Edit3->Text);
a=StrToFloat(Edit7->Text);
T=StrToFloat(Edit12->Text);
bool flag=false;
int notx,notu;
point xk,x1;
double up;
mas U;
mass X;
m x;
do
{
dt=T/N;
dx1=9.0/m1;
dx2=20.0/m2;
du=1.0/m3;
x=new sov [N+1];
X=new double* [2];
U=new double [N+2];
for (int i=0;i<=N;i++)
{
x[i].u=new double *[m1+1];
x[i].V=new double *[m1+1];
for (int j=0;j<=m1;j++)
{
x[i].u[j]=new double [m2+1];
x[i].V[j]=new double [m2+1];
}
}
for (int i=0;i<2;i++)
X[i]=new double [N+2];
for (int i=0;i<=m1;i++)
for (int j=0;j<=m2;j++)
x[N].V[i][j]=0;
for (int k=N-1;k>=0;k--)
{
notx=0;
for (int i=0;i<=m1;i++)
for (int j=0;j<=m2;j++)
{
x1.x=1+i*dx1;
x1.y=-10+j*dx2;
notu=0;
for (int n=0;n<=m3;n++)
{
up=n*du;
xk.x=f(x1.x,x1.y,up,0);
xk.y=f(x1.x,x1.y,up,1);
if (!D(xk)) notu+=1;
else
{
if (prok(xk).f)
{
i0=prok(xk).x;
j0=prok(xk).y;
double fn=Bk(x1.x,x1.y,up)+x[k+1].V[i0][j0];
if ((fn<x[k].V[i][j]) ||(n==0))
{
x[k].V[i][j]=fn;
x[k].u[i][j]=up;
}
}
else notu++;
}
}
if (notu==m3) notx+=1;
}
}
point b;
b.x=X[0][0]=5;
b.y=X[1][0]=2;
int i_,j_;
if (prok(b).f)
{
i_=prok(b).x;
j_=prok(b).y;
}
b.x=X[0][0]=5;
b.y=X[1][0]=2;
for (int k=0;k<N;k++)
{
if (prok(b).f)
{
i0=prok(b).x;
j0=prok(b).y;
U[k]=x[k].u[i0][j0];
b.x=X[0][k+1]=f(X[0][k],X[1][k],U[k],0);
b.y=X[1][k+1]=f(X[0][k],X[1][k],U[k],1);
}
}
J=I(X,U);
flag=true;
if ((fabs(J-x[0].V[i_][j_])<=eps)||((J-J_)<=eps)) flag=false;
else
{
J_=J;
m1=2*m1;
m2=2*m2;
m3=2*m3;
N=2*N;
}
}
while (flag);
Edit5->Text=FloatToStr(J);
StringGrid1->Cells[0][0]="dt";
StringGrid1->Cells[1][0]="x1(t)";
StringGrid1->Cells[2][0]="x2(t)";
StringGrid1->Cells[3][0]="u(t)";
for (int i=0;i<=N;i++)
{
StringGrid1->Cells[0][i+1]=FloatToStrF(i*dt,ffGeneral,5,2);
StringGrid1->Cells[1][i+1]=FloatToStrF(X[0][i],ffGeneral,5,2);
StringGrid1->Cells[2][i+1]=FloatToStrF(X[1][i],ffGeneral,5,2);
if (i%10==0)
{
Chart1->Series[0]->AddXY(StrToFloat(i*dt),StrToFloat(X[0][i]),"",clRed);
Chart1->Series[1]->AddXY(StrToFloat(i*dt),StrToFloat(X[1][i]),"",clBlue);
}
if (i!=N)
{
StringGrid1->Cells[3][i+1]=FloatToStrF(U[i],ffGeneral,5,2);
if (i%10==0)
{
Chart2->Series[0]->AddXY(StrToFloat(i*dt),StrToFloat(U[i]),"",clRed);
}
}
}
delete []X;
delete [] x;
delete []U;
}






