Проверка значимости и интервальные оценки параметров связи

Лабораторная работа №4

Корреляционно-регрессионный анализ.

 

Оценки параметров корреляционного анализа

Основная задача двумерного корреляционного анализа признаков (Х, Y) состоит в оценке пяти параметров:

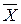- оценка среднего значения величины Х,

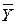- оценка среднего значения величины Y,

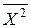- оценка среднего значения величины Х²,

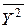- оценка среднего значения величины Y²,

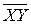- оценка среднего значения произведения величин Х и Y.

Откуда:

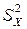
- оценка дисперсии величины Х,

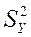
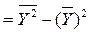- оценка дисперсии величины Y,

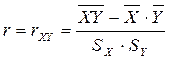- оценка для парного коэффициента корреляции.

Парный коэффициент корреляции служит мерой линейной статистической зависимости между величинами и является одним из основных показателей взаимосвязи между ними, принимающий значения от -1 до 1.

Имея эти показатели, можно получить уравнения линий регрессии, показывающих изменение условных математических ожиданий в зависимости от изменения соответствующих значений случайных переменных:

уравнение регрессии Y на X: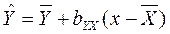

уравнение регрессии X на Y: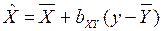

И тогда оценка коэффициентов уравнения регрессии

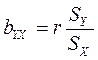
В двумерном случае для наглядности наносят на график точки (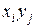) - корреляционное поле; строят эмпирическую регрессию – ломанную, соединяющую точки (), где 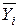- средне арифметическое наблюденных значений Y; оценки функции регрессии 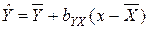(рисунок 4.1)

 

 

 

 

Рисунок 4.1

 

 

Проверка значимости и интервальные оценки параметров связи

 

Проверка значимости парного коэффициента корреляции.

С этой целью проверки гипотезы о значимости коэффициента корреляции выдвигают нулевую гипотезу Н₀: , при альтернативной гипотезе Н₁: 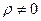. Для ее проверки используют статистику

(1)

Критическое значение t находят по таблицам распределения Стьюдента с 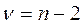степенями свободы и уровнем значимости α. Затем сравнивают наблюдаемое и критические значения. Если ‌‌‌‌t> t_кр, то гипотеза о незначимости коэффициента корреляции отвергается.

Интервальные оценки находят для значимых параметров связи:. При определении с надежностью γ доверительного интервала для ρ используют Z – преобразование Фишера:

(2)

t_γ вычисляют по таблице нормального распределения с заданным γ.

Значение Z_r определяют по таблице Z – преобразования по найденному значению r.

Обратный переход от Z кρ осуществляют также по таблицам Z – преобразования Фишера, после чего получают интервальную оценку для ρ:

 

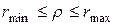. (3)

 

Значимость коэффициентов регрессии проверяют с использованием статистики:

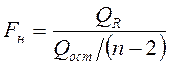, (4)

 

где

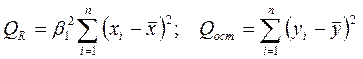(5)

которая при справедливости гипотезы 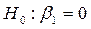распределена по закону Фишера – Снедекора с заданным уровнем значимости a и числом степеней свободы n ₁= n ₂= n -1

Интервальная оценка для коэффициентов регрессии имеет вид:

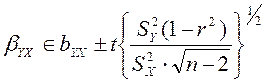(6)

Аналогично для коэффициента β _XY:

 

(7)