Лабораторная работа № 6. Модульная единица № 2.9
Определение удельной теплоёмкости твёрдого тела
Теоретическая часть
Теплоёмкостью называется способность тел накапливать тепловую энергию при их нагревании. Количество теплоты Q, необходимое для нагревания тела массы m от температуры t0 до t1, выражается соотношением
 , ,
| (1) |
где C – коэффициент пропорциональности, называемый удельной теплоёмкостью.
Удельной теплоёмкостью C называется количество теплоты, необходимое для нагревания единицы массы вещества на один градус; размерность C выражается в Дж/кг · град.
Мольной теплоёмкостью CM называется количество теплоты, необходимое для нагревания одного моля вещества на 1 градус. Если M – масса одного моля вещества, то справедливо соотношение CM = M · C [Дж/моль · град].
Процесс нагревания твёрдых тел отличается от нагревания газообразных веществ (см. работу 12) тем, что у них коэффициент объёмного расширения значительно меньше, поэтому затрачиваемая теплота идёт в основном на увеличение внутренней энергии тела, а совершение работы за счёт расширения пренебрежимо мало, следовательно в этом случае можно говорить просто о теплоёмкости твёрдого тела (аналогично CV для газов).
В отличие от газов в твёрдых телах атомы связаны упруго с положениями равновесия, которыми являются узлы кристаллической решётки. Поступательных и вращательных степеней свободы у атомов твёрдого тела нет. Внутренняя энергия твёрдых тел возрастает при нагревании за счёт возбуждения колебательных степеней свободы – колеблющиеся атомы в некотором приближении можно рассматривать как гармонические осцилляторы.
Согласно представлением классической статической физики на каждую колебательную степень свободы приходится в среднем энергия E = kT, а на каждую поступательную и вращательную степень свободы приходится в среднем кинетическая энергия, равная кТ/2.
Это обусловливается тем, что при колебаниях атома у него есть и кинетическая, и потенциальная энергии, причем их средние значения равны.
Так как каждый атом колеблется по трем осям х, у, z, то полная энергия колебаний одного атома будет равна
Ek = 3kT.
Внутреннюю энергию одного моля простого вещества находим, умножая число Авогадро NA = 6,02 · 1023 1/моль на Eк, тогда имеем ЕМ = ЕкNА = 3kTNA = 3RT, где R - универсальная газовая постоянная..
При изменении температуры нагреваемого тела на ΔT = T1 – T0 градусов приращение внутренней энергии равно ΔЕМ = 3RΔT, а мольная теплоёмкость
 . .
| (2) |
Поскольку R ≈ 8,31 Дж/моль · К, то мольная теплоёмкость простых веществ равна 3R≈ 25 Дж/моль · К, что составляет правило Дюлонга–Пти.
Эксперимент показывает достаточно хорошее соответствие этого правила для многих веществ: для серебра и алюминия CM = 3,1R, для золота и железа CM = 3,22R. Поскольку в ионных решётках двухатомных соединений типа солей на один моль приходится 2NA атомов, то мольная теплоёмкость таких веществ равна CM = 2 CM. Например, для поваренной соли (NaCl) CM2 = 6,1R, что также хорошо согласуется с теорией.
Правило Дюлонга–Пти выполняется в том случае, когда теплоёмкость не зависит от температуры. Этот диапазон температур для многих веществ достаточно широк, но при очень низких температурах теплоёмкость уменьшается, а при весьма высоких – возрастает. Скачки величины теплоёмкости при увеличении температуры связаны с появлением новых степеней свободы, возбуждаемых при подводе энергии в процессе нагревания тел.
Общая постановка задачи:
Определить удельную теплоёмкость твёрдых тел калориметрическим методом, вычислить величины мольной теплоёмкости этих тел. Объяснить полученные результаты на основе молекулярно-кинетической теории.
Список индивидуальных данных:
нагреватель, 2) калориметр, 3) термометр, 4) мерная мензурка, 5) исследуемые тела, 6) инженерный калькулятор.
Пример выполнения работы
Один из методов определения теплоёмкости твёрдых тел основан на теплообмене исследуемого тела с веществом, теплоёмкость которого известна. Для этого удобно пользоваться жидкостью, удельная теплоёмкость которой в данном интервале температур постоянна и известна.
Если температура тела и жидкости различна, то при контакте между ними начинается теплообмен, и идёт до тех пор, пока температура системы «тело – жидкость» не выровняется. Уравнение теплового баланса очевидно:
Q1 = Q2,
где Q1 – тепло, отданное телом, и Q2 – тепло полученное жидкостью. Уравнение баланса справедливо в условиях изолированной системы.
Контролируемый теплообмен осуществляется с помощью калориметров, – в этом случае в уравнение теплового баланса нужно добавить члены, учитывающие вклад материала калориметра и сопутствующих принадлежностей.
Простейший калориметр состоит из (рисунок) металлического стакана 1, помещённого в другой 2 на теплоизолирующих пробках 3. Воздушный зазор 4 уменьшает теплообмен с внешней средой. В малый стакан наливают воду известного объёма 5, а для измерения температуры применяют термометр 6. Для лучшего теплообмена между водой и изучаемым телом 7 служит мешалка 8.
Уравнение теплового баланса запишем в виде
 , ,
| (3) |
где Q1 и Q2 (см. выше), а Q3 – количество теплоты, полученное корпусом калориметра и мешалкой, Q4<<Q3 – тепло, полученное термометром. С учётом уравнения (1) перепишем (3) в виде
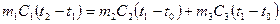 , ,
| (4) |
где m1 – масса исследуемого тела, C1 – его удельная теплоёмкость, t2 – температура тела в начале опыта, равная в данном случае температуре кипения воды, t1 – конечная температура системы «тело-калориметр», m2 – масса воды, m3 – масса деталей калориметра, С2 – удельная теплоёмкость воды, С3 – удельная теплоёмкость материала калориметра; С2 = 4,2 · 103, С3 = 3,8 · 102 Дж/кг · град; t0 – температура воды в начале опыта.

Рис. Схематическое изображение калориметра
Тогда искомая величина С1 равна
 , ,
| (5) |
где k = m2C2 +m3C3 – константа прибора
Определение удельной теплоёмкости твёрдых тел
1) Исследуемое тело опускают в нагреватель с кипящей водой и прогревают около 10 минут.
2) Мерной мензуркой отмеривают 300мл воды и вливают её в малый стакан калориметра; погрешность измерения ΔV = 0,5мл.
3) Измеряют температуру воды t0 термометром; погрешность измерения Δt1 = 0,5˚С. Будем считать t2 = 100ºC, Δt2 = 1ºC
4) Быстро вынимают исследуемое тело из нагревателя и переносят в калориметр. Постоянно перемешивая мешалкой воду, наблюдают за установлением температуры, и при достижении её постоянства снимают данные t1 и заносят в таблицу.
5) Вычисляют аппаратурный параметр k, согласно данным, написанным на стакане калориметра (масса) и величинам С2 и С3 (см. формулу (4)):
| k = m2C2 + m3C3; m2 = 0,3 кг | (6) |
6) Величину абсолютной погрешности Δk вычисляют по формуле
 , ,
| (7) |
считая Δm3 = 0,1г или Δm3 = 0,1 × 10-3 кг; Δm = 0,5 × 10-3 кг.
7) Определяют величину С1 по формуле (5)
8)величину относительной погрешности вычисляют по формуле
δс1 = √δк2+ δm12 + δ2t1+ δt22 (8)
где δк = Δk/k, δm1 = Δm1/m; Δm1 = 10-4 кг.
δt1 = Δt1/(t1 – t0), δt2 = Δt2/(t2 – t1) (9)
9) Абсолютную ошибку ΔС определения удельной теплоёмкости первого образца находят по формуле ΔС1 = δС1×С1. Все результаты записывают в таблицу.
10) Аналогичные операции и измерения проделывают со вторым образцом и результаты также вносят в таблицу.
11) Окончательный результат представляют в виде (удельная теплоёмкость)
| С1±ΔC1 и С2±ΔC2, | (10) |
а также пересчитывают по формуле СМi = Мi · Сi и выражают в виде (мольные теплоёмкости)
| СM1±ΔCM1 и CM2±ΔCM2. | (11) |
12) Полученные данные сравнивают с теоретической величиной мольной теплоёмкости твёрдых тел СМ ≈ 25 Дж/моль · град и делают соответствующие выводы.
Определение теплоёмкости твёрдых тел
Таблица
| № | t0, ˚С | t1, ˚С | t2, ˚С | k | Δk | C, Дж/кг · град | ΔC, Дж/кг · град | М, кг/ моль | См |
| Металл 1 (Fe) | |||||||||
| Металл 2 (Al) |
Контрольные вопросы к защите
1. Какая физическая величина измеряется в данной работе и какова единица ее измерения?
2. Какому типу измерений относиться измерение температуры?
3. Оцените точность измерения температуры?
4. Что называется удельной и мольной теплоёмкостью?
5. Почему при изучении теплообмена используется колориметр?
6. Описать устройство калориметра, записать условие теплового баланса.
7. Между какими частями системы вода – калориметр – нагретое тело происходит теплообмен?
8. Что утверждает правило Дюлонга–Пти, раскрыть его физический смысл.
9. Как определяется мольная теплоёмкость для двухатомных кристаллических веществ?
10. Чем определяется погрешность окончательного результата при определении удельной теплоёмкости?
Способ оценки результатов
Полный ответ на каждый вопрос оценивается в один балл.






