СМО состоит из одного прибора и очереди; в системе может одновременно находиться не более, чем n требований; очередь упорядоченная. Обозначим через X(t) число требований, находящихся в системе в момент t. Функция X(t) принимает (n+1) значение: x0 – в системе нет требований, x1 – в системе одно требование, …, xn – в системе n требований.
Определим вектор вероятности p(t) = [p0(t), P1(t), …, pn(t)] состояний системы для любого момента времени t, где pq(t) – вероятность того, что функция X(t) в момент времени t принимает значения xq, q = 0, 1, …, n. заменим непрерывное время t прерывным, меняющимся скачкообразно через интервал Δt и сведем, тем самым, X(t) к простой цепи Маркова. Составим матрицу вероятностей перехода pqq (t, t+Δt) из состояния xq в момент t в состояние xq, в момент (t, t+Δt) при условии, что Δt мало.
Вследствие ординарности входящего потока и показательного закона распределения времени обслуживания за малый интервал Δt не может произойти соответственно более одного поступления и более одного окончания обслуживания. Поэтому в интервале (t, t+Δt) могут произойти следующие переходы:

Определим вероятности следующих событий:
1) за интервал (t, t+Δt) в систему не поступит ни одного требования;
2) за интервал (t, t+Δt) прибор не закончит обслуживания.
Вероятность первого события
 вероятность второго события
вероятность второго события

Тогда вероятность поступления в систему ровно одного требования за интервал (t, t+Δt) и вероятность того, что за интервал (t, t+Δt) прибор обслужит ровно одно требование равны: 1-(1-λ Δt)= λ Δt и 1-(1µΔt)=µΔt, как вероятности событий, противоположных рассмотренным.
Вычислим вероятность pqq (t, t+Δt), где n>q>0. Eсли в момент t в системе находилось q требований, то событие, состоящее в том, что в момент t+Δt в системе по-прежнему будет находиться q требований, можно рассматривать как сумму следующих несовместных событий:
события А – за интервал (t+Δt) ни одно требование не поступило в систему и ни одно требование не было обслужено Р(А)≈ (1-λ Δt)(1-µΔt);
события B – за интервал (t+Δt) в систему поступило ровно одно требование и за это же время прибор закончил обслуживание одного требования и оно покинуло систему. P(B)≈λ∆t*μ∆t.
Таким образом,

так как 2λµΔt2 является величиной бесконечно малой более высокого порядка, чем Δt. Рассуждая аналогично, можно определить и другие вероятности перехода pqq (t, t+Δt).
| Переход | Вероятность |
 
| 
|
Так как вектор вероятностей простой цепи Маркова в момент времени ti равен произведению вектора вероятностей в момент времени t(i-1) на матрицу переходов, получим систему уравнений:
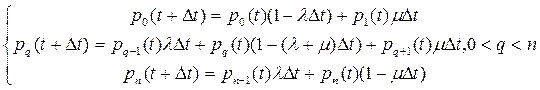
Разделим на ∆t и перейдем к пределу при ∆t→0.
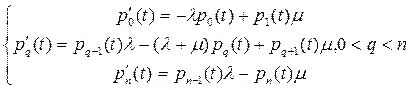
Для системы, проработавшей длительное время,

тогда

Из первого уравнения  .
.
Из второго, учитывая последнее равенство,

Аналогично, из третьего уравнения находим

Таким образом,

Подставим полученное уравнение в последнее равенство системы:
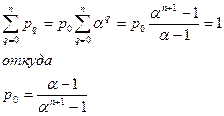

Вычислим основные вероятностные характеристики системы:
1. Математическое ожидание числа требований в системе.

2. Математическое ожидание числа требований в узле обслуживания.
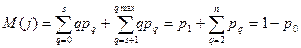
s – число приборов;
qmax – максимальное число требований в системе.
3. Математическое ожидание числа требований в очереди

4. Математическое ожидание числа свободных приборов

5. Вероятность отказа

Пример.
Перед обслуживающим прибором расположен накопитель, в который поступают заявки. Если в накопителе уже находятся 2 заявки, то очередная передается на другой прибор. Интенсивность потока заявок – 2 заявки в минуту, среднее время обслуживания – 20с, n=3. Вычислить основные вероятностные характеристики системы.
Решение.







