ЛАБОРАТОРНАЯ РАБОТА №7
ОЦЕНКА ЭФФЕКТИВНОСТИ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ.
Общие понятия теории массового обслуживания.
Основной задачей теории массового обслуживания является установление количественных зависимостей между числом приборов обслуживания, характеристиками входящего потока требований (заявок) и качеством обслуживания. При этом под качеством обслуживания понимается, насколько своевременно проведено обслуживание поступивших в систему требований, насколько полно загружены обслуживающие приборы, не велик ли уход из системы не обслуженных требований, не создается ли большая очередь.
Каждая СМО состоит из какого – то количества обслуживающих единиц, которые называются каналами обслуживания (это станки, транспортные тележки, роботы, линии связи, кассиры, продавцы и т.д.). Всякая СМО предназначена для обслуживания какого – то потока заявок (требований), поступающих в какие – то случайные моменты времени.
Обслуживание заявки занимает случайное время, после чего канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени обслуживания может привести к тому, что в какие – то периоды времени на входе СМО скапливается излишне большое количество заявок (они либо становятся в очередь, либо покидают СМО необслуженными). В другие же периоды СМО будет работать с недогрузкой или вообще простаивать.
Предмет теории массового обслуживания – построение математических моделей, связывающих заданные условия работы СМО (число каналов, их производительность, правила работы, характер потока заявок) с показателями эффективности СМО. Эти показатели описывают способность СМО справляться с потоком заявок. Ими могут быть: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди; среднее время ожидания обслуживания и т.д.
Классификация систем массового обслуживания
По своему составу СМО делятся на системы с одним обслуживающим прибором (каналом) и многими приборами обслуживания, называющимися соответственно одноканальными и многоканальными.
Многоканальные системы могут состоять из однотипных или разнотипных приборов.
По времени пребывания требований в системе до начала обслуживания СМО делятся на:
- системы с отказами
- системы с неограниченным временем ожидания
- системы смешанного типа (с ограниченным временем ожидания).
В системах с отказами всякое поступившее требование, застав все приборы занятыми, покидает систему.
В системах с неограниченным временем ожидания поступившее в систему требование и обнаружившее все приборы занятыми вынуждено ожидать своей очереди до момента освобождения какого-нибудь (или определенного прибора).
В системах смешанного типа поступившие требования, застав все приборы занятыми, становятся в очередь. Но в ней они находятся ограниченное время, по истечении которого покидают систему. К смешанным системам относятся также системы с ограниченной длиной очереди.
Поток событий – последовательность однородных или неоднородных событий, которые наступают через случайные промежутки времени. Случайные временные интервалы между наступлениями событий в потоке в потоке могут подчиняться различным законам распределения. В большинстве работ по теории массового обслуживания, особенно прикладного характера, рассматривается пуассоновский (простейший) поток, в котором вероятность поступления в промежуток времени t ровно k требований задается формулой Пуассона.
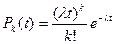
где λ – плотность потока требований.
Простейший поток теории массового обслуживания играет такую же роль, как нормальный закон распределения случайных величин в теории вероятностей.
Простейший поток обладает тремя основными свойствами: стационарностью, отсутствием последействия и ординарностью.
Случайный поток называется стационарным, если вероятность поступления определенного количества требований в течение определенного отрезка времени зависит от его (отрезка) величины и не зависит от начала его отсчета на оси времени, то есть зависит от величины времени τ и не зависит от положения этого интервала на временной оси.

Отсутствие последействия состоит в том, что вероятность поступления за отрезок времени τ определенного числа требований не зависит от того, сколько требований уже поступило в систему, т.е. не зависит от предыстории изучаемого явления. Отсутствие последействия предполагает взаимную независимость протекания процесса в не перекрывающиеся между собой промежутки времени. Другими словами, это означает, что события, образующие поток, появляются в те или иные моменты времени независимо друг от друга и вызваны каждое своими собственными причинами.
Ординарность потока требований означает практическую невозможность появления двух и более требований в один и тот же момент времени.
Важной характеристикой потока является его интенсивность, которая определяется как математическое ожидание числа требований, поступающих за единицу времени. Интенсивность потока событий – это среднее число событий, приходящееся на единицу времени.
Показатели эффективности обслуживающих систем.
Показатели эффективности завися от 3 групп факторов: характеристик качества и надежности системы; экономических показателей (стоимости системы, трудовых затрат обслуживающего персонала, убытков, связанных с несвоевременным обслуживанием и т.д.); особенностей ситуации, в которой обслуживается система (параметров потока требований, ограничений на длину очереди и т.д.).
В зависимости от условий эксплуатации системы и принятого показателя эффективности выбирается математическая модель процесса.
Наиболее часто применяемые показатели:
- вероятность потери требования (pn);
- вероятность того, что обслуживанием занято к приборов (pk);
- среднее число занятых приборов, характеризующая степень загрузки СМО:
 ;
;
- среднее число свободных приборов:
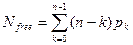
- коэффициент простоя приборов

- коэффициент занятости оборудования:

- среднее время ожидания требований в очереди до начала обслуживания:
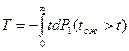
где

где Pk(tож>t) – условная вероятность того, что время ожидания больше t, при условии, что в момент поступления требования в ней обслуживались к требований.
- вероятность того, что время ожидания в очереди не продлится больше определенной величины:
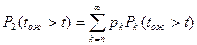
- средняя длина очереди:
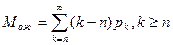
где pk – вероятность того, что в системе находится к требований.
Кроме указанных, могут использоваться стоимостные показатели, такие как: стоимость обслуживания каждого требования, стоимость потерь, связанных с простаиванием требований в очереди в единицу времени, стоимость убытков, связанных с уходом требований из очереди, стоимость эксплуатации приборов в единицу времени, стоимость единицы времени простоя прибора.
Используются следующие экономические показатели качества:
1. Стоимость потерь для систем с ожиданием:

где
qож – стоимость потерь, связанных с ожиданием в очереди в единицу времени;
qпр – стоимость единицы времени простоя прибора;
qbusy – стоимость эксплуатации прибора в единицу времени;
Для системы с отказами:

Для смешанной системы:







