Постановка задачи.
Общая задача: из курса теоретической механики известно, что в соответствии принципом Деламбера неустановившееся движение тела описывается вторым законом Ньютона. Поскольку в данной задаче рассчитывается движение лишь в направлении одной из осей координат (в данном случае оси " t "), то достаточно записать уравнения движения в проекции на ось " t " и решать его относительно скорости V в направлении оси " t " и пройденного по этой координате пути S.
Математическая модель неустановившегося движения судна:
Основным уравнением задачи в этом случае является уравнение второго закона Ньютона в проекции на ось координат " t ".
ma=F (1)
Здесь
m - масса тела (судна)
a=dV/dt - ускорение судна
F - сумма всех сил, действующих на судно, в проекции на ось " t".
F=R+T (1’)
R -сопротивление воды движению судна;
Т - тяга движителя (как правило, гребного винта).
Из физических соображений понятно, что сопротивление R зависит от скорости движения (чем больше скорость V, тем больше сопротивление R) и направлена против скорости V, т.е. в отрицательном направлении оси " t ". При решении задач необходимо учитывать, что во время стоянки судна V =0 и R(V)= 0.
Тяга, создаваемая гребным винтом, также зависит от скорости движения судна, но действует в противоположном силе сопротивления R направлении, т.е. направлена в положительном направлении оси " t ". С учетом сказанного, уравнение (1) можно записать в виде:
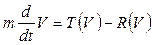(2)
Таким образом, получено обыкновенное дифференциальное уравнение 1-го порядка относительно скорости движения судна V.
Для определения пройденного за время разгона пути S к этому уравнению (2) необходимо добавить уравнение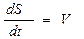 
, являющееся определением понятия - "скорость".
Следовательно, математическая модель задачи - система из двух дифференциальных уравнений 1-го порядка, записанных в каноническом виде:
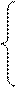
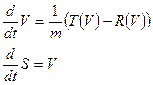(3)
Здесь функции R(V) и T(V) являются заданными и находятся по испытаниям моделей судна и гребного винта. В данной курсовой работе эти функции задаются графически. Точка их пересечения является скоростью постоянного движения. Для решения системы уравнений (3) необходимо задать начальные условия: t0=0, V0=0 или V=VH.
Методика и алгоритмы решения задачи.
Решение задачи курсовой работы разделяется на три модельных задачи(МЗ). Все МЗ выполняются в пакетах Excel и MathCAD. В каждой из эти модельных задач необходимо сначала выполнить аппроксимацию исходных данных.
Аппроксимация исходных данных:
• выбрать класс аппроксимирующей функции (если выбран полином, то необходимо выбрать
его степень исходя из вида кривой по характерным точкам, выбранным из контрольных);
• определить коэффициенты аппроксимации;
• рассчитать и вывести на дисплей графики аппроксимирующих функций.
Также для каждой МЗ необходимо найти:
- стационарную скорость Vст из уравнения R(V) = T(V), которое необходимо решить методом Ньютона, а также представить блок-схему и программу на языке программирования Фортран;
- найти время разгона tp, решив интеграл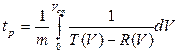 
методом Симпсона, а также представить блок-схему и программу на языке программирования Фортран;
-решив систему дифференциальных уравнений (3) первой модификацией метода Эйлера найти путь разгона Sp;
-определить время торможения tт;
-определить путь торможения tт;
-определить энергию разгона Ep из соотношения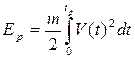 
;
Первая модельная задача.
-линейная аппроксимация полиномом первой степени для функций R(V) и T(V) на всем участке изменения V.
Вторая модельная задача.
-кривую R(V) аппроксимируем кусочно-линейно на трех участках, а T(V) –на одном.
Третья модельная задача.
-кривую R(V) и T(V) аппроксимируем полиномом четвертой степени–на всем участке.
3.Формирование исходных данных.
В курсовой работе исходными данными являются функции R(V) и T(V), которые представлены в графическом виде (рис.1) при мощности движителя 1800 об/мин.
Массу судна выбираем равной порожнему водоизмещению СПК «Белорусь»:
m= 9.6 Т =9600 кг
