Метод простой итерации
Метод Ньютона (метод касательных)
Метод Гауса Пусть исходная система выглядит следующим образом

Матрица A называется основной матрицей системы,b— столбцом свободных членов.Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных  .Тогда переменные
.Тогда переменные  называются главными переменными. Все остальные называются свободными. Если хотя бы одно число
называются главными переменными. Все остальные называются свободными. Если хотя бы одно число  , где
, где  , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.Пусть
, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.Пусть  для любых
для любых  .Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x (
.Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x ( , где
, где  — номер строки):
— номер строки):
 ,
,
где  Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
8.Постановка задачи численного решения СЛАУ.Прямые методы решения.Метод LU-разложения (алгоритм, трудоёмкость и критерий примнимости).Матрица перестановок.
Численное решение уравнений и их систем состоит в приближённом определении корня или корней уравнения или системы уравнений и применяется в случаях, когда точное значение вычислить невозможно или очень трудоёмко.
 или
или 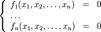
Численное решение задачи можно проводить как непосредственно (используя одноимённые методы), так и с применением оптимизационных методов, приведя задачу к соответствующему виду.
1. Метод последовательных приближений 2. Метод Гаусса-Зейделя 3. Метод обращения матрицы 4. Триангуляция матрицы
5. Метод Халецкого 6. Метод квадратного корня
LU-разложение — представление матрицы A в виде произведения двух матриц, A=LU, где L— нижняя треугольная матрица, а—U верхняя треугольная матрица. LU-разложение еще называют LU-факторизацией. LU-разложение используется для решения систем линейных уравнений, обращения матриц и вычисления определителя.Этот метод является одной из разновидностей метода Гаусса.
LU-разложение может быть использовано для решения системы линейных уравнений Ax=b, где A— матрица коэффициентов системы, x— вектор неизвестных величин системы,b— вектор правых частей системы.Если известно LU-разложение матрицы A, A=LU, исходная система может быть записана как LUx=bЭта система может быть решена в два шага. На первом шаге решается система 
Поскольку L— нижняя треугольная матрица, эта система решается непосредственно прямой подстановкой. На втором шаге решается система Ux=y. Поскольку U— верхняя треугольная матрица, эта система решается непосредственно обратной подстановкой.
Ма́трица перестано́вки (или подстано́вки) — квадратная бинарная матрица, в каждой строке и столбце которой находится лишь один единичный элемент. Каждая матрица перестановки размера  является матричным представлением перестановки порядка
является матричным представлением перестановки порядка 
Определение Пусть дана перестановка  порядка
порядка  :
: 
Соответствующей матрицей перестановки является матрица  вида:
вида:  где
где  — вектор длины n, i-й элемент которого равен 1, а остальные равны нулю.
— вектор длины n, i-й элемент которого равен 1, а остальные равны нулю.
9.Постановка задачи численного решения СЛАУ.Прямые методы решения.Матрица Хаусхольдера, QR-разложение.Метод отражений.Матрица Гивенса и метод вращений.
Численное решение уравнений и их систем состоит в приближённом определении корня или корней уравнения или системы уравнений и применяется в случаях, когда точное значение вычислить невозможно или очень трудоёмко.
 или
или 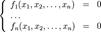
Численное решение задачи можно проводить как непосредственно (используя одноимённые методы), так и с применением оптимизационных методов, приведя задачу к соответствующему виду.
1. Метод последовательных приближений
2. Метод Гаусса-Зейделя
3. Метод обращения матрицы
4. Триангуляция матрицы
5. Метод Халецкого
6. Метод квадратного корня
Пусть гиперплоскость описывается единичным вектором u, который ортогонален ей, а  — скалярное произведение в V, тогда
— скалярное произведение в V, тогда
 называется оператором Хаусхолдера.
называется оператором Хаусхолдера.
Матрица Хаусхолдера имеет вид: H=I-2uu*
- Матрица Хаусхолдера является эрмитовой: H=H*
- Матрица Хаусхолдера является унитарной: H*H=I
- Значит она является инволюцией:
 .
. - Преобразование
 отображает точку x в точку x-2(u,x)u
отображает точку x в точку x-2(u,x)u - Преобразование Хаусхолдера имеет одно собственное значение равное (-1), которое отвечает собственному вектору u, все другие собственные значения равны (+1).
- Определитель матрицы Хаусхолдера равен (-1).
QR-разложение матрицы — представление матрицы в виде произведения унитарной (или ортогональной матрицы) и верхнетреугольной матрицы.Матрица A размера nxn с комплексными элементами может быть представлена в виде: A=QR, где Q-— унитарная матрица размера nxn, а R— верхнетреугольная матрица размера nxn.В частном случае, когда матрица A состоит из вещественных чисел, Q является ортогональной матрицей (то есть  , где I— единичная матрица).По аналогии, можно определить варианты этого разложения: QL-, RQ-, и LQ-разложения, где L— нижнетреугольная матрица.Если A— квадратная невырожденная матрица, то существует единственное QR-разложение, если наложить дополнительное условие, что элементы на диагонали матрицы R должны быть положительными вещественными числами.
, где I— единичная матрица).По аналогии, можно определить варианты этого разложения: QL-, RQ-, и LQ-разложения, где L— нижнетреугольная матрица.Если A— квадратная невырожденная матрица, то существует единственное QR-разложение, если наложить дополнительное условие, что элементы на диагонали матрицы R должны быть положительными вещественными числами.
Матрица Гивенса. Поворот Гивенса вектора на плоскости определяется матрицей линейного оператора: 
Поэтому для некоторого вектора  :
:  . К примеру, для
. К примеру, для  :
: 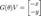
10.Постановка задачи численного решения СЛАУ.Метод простой итерации.Методы Якоби, Зейделя и релаксаци.Свойство независимости погрешности от числа итераций.
Численное решение уравнений и их систем состоит в приближённом определении корня или корней уравнения или системы уравнений и применяется в случаях, когда точное значение вычислить невозможно или очень трудоёмко.
 или
или 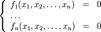
Численное решение задачи можно проводить как непосредственно (используя одноимённые методы), так и с применением оптимизационных методов, приведя задачу к соответствующему виду.
Метод простых итераций в общем виде. Заменим исходное уравнение  на эквивалентное
на эквивалентное  ,и будем строить итерации по правилу
,и будем строить итерации по правилу  . Таким образом метод простой итерации - это одношаговый итерационный процесс. Для того, что бы начать данный процесс, необходимо знать начальное приближение
. Таким образом метод простой итерации - это одношаговый итерационный процесс. Для того, что бы начать данный процесс, необходимо знать начальное приближение  .
.
Метод якоби
Для того, чтобы построить итеративную процедуру метода Якоби, необходимо провести предварительное преобразование системы уравнений 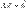 к итерационному виду
к итерационному виду  . Оно может быть осуществлено по одному из следующих правил:
. Оно может быть осуществлено по одному из следующих правил:
где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A, а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A, на главной диагонали которых нули,E— единичная матрица.Тогда процедура нахождения решения имеет вид: 
Чтобы пояснить суть метода, перепишем задачу в виде:
 Здесь в j-м уравнении мы перенесли в правую часть все члены, содержащие
Здесь в j-м уравнении мы перенесли в правую часть все члены, содержащие  , для i>j. Эта запись может быть представлена:
, для i>j. Эта запись может быть представлена:

где в принятых обозначениях D означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы A, а все остальные нули; тогда как матрицы U и L содержат верхнюю и нижнюю треугольные части A, на главной диагонали которых нули.
Итерационный процесс в методе Гаусса-Зейделя строится по формуле  после выбора соответствующего начального приближения
после выбора соответствующего начального приближения  .
.
Метод Гаусса-Зейделя можно рассматривать как модификацию метода Якоби. Основная идея модификации состоит в том, что новые значения  используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:
используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:

где  . Таким образом, i-тая компонента
. Таким образом, i-тая компонента 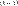 -го приближения вычисляется по формуле:
-го приближения вычисляется по формуле:

Метод релаксации - итерационный метод решения систем линейных алгебраических уравнений.
Система линейных уравнений
13.Приближенное вычисление производных. Построение конечно разностных формул численного дифференциирования и оценка их точности. Метод неопределённых коэфицентов.
Пусть Kn - система узловых точек a = x0 < x1 <…< xn = b. Функция Sk(x) называется сплайн-функцией Sk(x) степени k≥0 на Kn, если
а) Sk(x) є Ck-1([a, b]) б) Sk(x) - многочлен степени не большей k; Сплайн-функция Ŝk(x) є Sk(Kn) называется интерполирующей сплайн-функцией, если Ŝk(xj) = f(xj) для j = 0,1,…,n В приложениях часто бывает достаточно выбрать k=3 и применить т. н. кубическую интерполяцию.
 Т. к. s(x) на каждом частичном интервале есть многочлен третьей степени, то для x є [xj-1,xj]
Т. к. s(x) на каждом частичном интервале есть многочлен третьей степени, то для x є [xj-1,xj]

 Здесь s2j, cj1, cj0 неизвестны для j = 1, 2, …, nПоследние исключаются в силу требования s(xj) = yj:
Здесь s2j, cj1, cj0 неизвестны для j = 1, 2, …, nПоследние исключаются в силу требования s(xj) = yj: 
 Дифференцируя эту функцию и учитывая, что s'(x) на всем интервале и, следовательно, в частности, в узлах должна быть непрерывна, окончательно получаем систему уравнений:
Дифференцируя эту функцию и учитывая, что s'(x) на всем интервале и, следовательно, в частности, в узлах должна быть непрерывна, окончательно получаем систему уравнений:

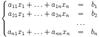 приводится к виду
приводится к виду  где
где  ,
, 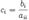
Находятся невязки  :
:

Выбирается начальное приближение  . Н а каждом шаге необходимо обратить в ноль максимальную невязку:
. Н а каждом шаге необходимо обратить в ноль максимальную невязку:  . Условие остановки:
. Условие остановки:  . Ответ находится по формуле:
. Ответ находится по формуле:  .
.
14.Понятие о численном решении задачи Коши для систем ОДУ. Понятие устойчивости, аппроксимаци и сходимости дискретных систем, теорема В.С. Рябенького-П.Лакса.Методы Эйлера и Рунге-Кутта.
Постановка задачи Коши
Метод Рунге-Кутта относится к методам численного решения обычных дифференциальный уравнений первого порядка. Этот численный метод является одним из точных методов численного решения ОДУ и систем ОДУ, и не очень сложных в реализации, поэтому этот медот получил широкое распространение. Задача Коши для ОДУ первого порядка ставится следующим образом: dy/dx=F(x,y).Как и для любых других чесленных методов решения дифференциальных уравнений, для решения этого уравнения требуется задать начальные условия: x0, y0. Математическое решение задачи Решением поставленной задачи будет ряд точек на плоскости (x,y). Обозначим шаг вычислений как h. Вектор точек по оси x обозначим x[i], i=0...N, при этом значения этого вектора будут определяться следующим образом: x[i]=x[0]+h*i. Вектор точек по оси y обозначим как y[i]. Тогда значения ветора y будут определяться следующим образом:
y[i+1]=y[i]+delta;
delta=(K1+2*K2+2*K3+K4)/6;
K1=h*F(x[i],y[i]);
K2=h*F(x[i]+h/2,y[i]+K1/2);
K3=h*F(x[i]+h/2,y[i]+K2/2);
K4=h*F(x[i]+h,y[i]+K3);
Таким образом будет получено численное решение исходного дифференциального уравнения на интервале [a,b] с заданными начальными условиями и шагом. Аппроксимация – процесс подбора эмпирической функции φ(х) для установления из опыта функциональной зависимости y= φ(х). Основная задача аппроксимации – построение приближенной (аппроксимирующей) функции наиболее близко проходящей около данных точек или около данной непрерывной функции.
Теорема Лакса-Рябенького
Из аппроксимационности и устойчивости решения следует его сходимость в случае линейных дифференциальных уравнений.
Метод Эйлера Пусть дана задача Коши для уравнения первого порядка 

где функция f определена на некоторой области  . Решение разыскивается на интервале
. Решение разыскивается на интервале  . На этом интервале введем узлы
. На этом интервале введем узлы 
Приближенное решение в узлах  , которое обозначим через
, которое обозначим через  определяется по формуле
определяется по формуле  Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
Эти формулы обобщаются на случай систем обыкновенных дифференциальных уравнений.
Классический метод Рунге — Кутты четвёртого порядка
Метод Рунге — Кутты четвёртого порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты.
Рассмотрим задачу Коши 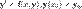
Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:  Вычисление нового значения проходит в четыре стадии:
Вычисление нового значения проходит в четыре стадии: 



где h — величина шага сетки по x.
Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок 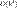 (ошибка на каждом шаге порядка
(ошибка на каждом шаге порядка 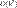 ).
).









