Вопросы для подготовки к тестированию:
1. Сформулируйте определение производной функции. Каков ее геометрический, экономический и механический смысл?
2. Запишите формулы производных суммы, произведения, частного двух функций. Приведите примеры.
3. Запишите формулу дифференцирования сложной функции.
4. Запишите формулы дифференцирования степенной, показательной, логарифмической и тригонометрических функций.
5. Как находится производная обратной и неявной функции?
6. Как находится производная функции, заданная параметрическими уравнениями?
7. Сформулируйте определение дифференциала функции.
8. Сформулируйте определения производной и дифференциала высших порядков.
9. Сформулируйте правило Лопиталя для раскрытия неопределенностей вида  .
.
10. Сформулируйте достаточное и необходимое условия возрастания и убывания функции.
11. Сформулируйте определение точки экстремума функции.
12. Дайте определение критической (стационарной) точки.
13. Сформулируйте первое и второе достаточные условия экстремума.
14. Как найти наибольшее и наименьшее значение функции на отрезке?
15. Сформулируйте условия выпуклости функции.
16. Что называется асимптотой графика функции?
17. Как определить вертикальные и наклонные асимптоты?
18. Изложите схему общего исследования функции и построения ее графика.
Задачи для подготовки к тестированию:
1. Вычислить производные следующих функций:
а)  ; б)
; б) 
Ответ: а)  ; б)
; б) 
2. Вычислить производные сложных функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  ;
;
Ответ: а) 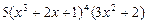 ; б)
; б) 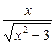 ;
;
в)  г)
г)  ; д)
; д)  ; е)
; е)  .
.
3. Составить уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой  .
.
Ответ:  .
.
4. Найти производную функции  , заданной неявно
, заданной неявно  .
.
5. Найти дифференциалы следующих функций:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Ответ: а)  ; б)
; б)  ; в)
; в)  ;
;
г) 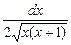 .
.
6. Вычислить пределы, используя правило Лопиталя:
а) 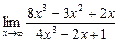 ; б)
; б)  ; в)
; в) 
Ответ: а) 2; б) 27; в) 1/9
7. Определить промежутки возрастания и убывания следующих функций:а)  ; б)
; б)  ; в)
; в)  .
.
Ответ: а)  – возрастает; б)
– возрастает; б) 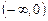 – возрастает,
– возрастает,  – убывает; в)
– убывает; в)  – возрастает,
– возрастает,  – убывает
– убывает
8. Исследовать функции на экстремум:
а) 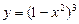 ; б)
; б)  г)
г)  .
.
Ответ: а)  – максимум; б)
– максимум; б) 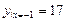 – максимум,
– максимум,  – минимум; г)
– минимум; г)  – минимум,
– минимум,  – максимум.
– максимум.
9. Определить интервалы выпуклости и найти точки перегиба следующих функций:
а)  ; б)
; б) 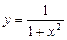 .
.
Ответ: а)  – интервал выпуклости вверх,
– интервал выпуклости вверх, 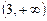 – интервал выпуклости вниз; б)
– интервал выпуклости вниз; б)  – интервал выпуклости вверх,
– интервал выпуклости вверх,  – интервалы выпуклости вниз,
– интервалы выпуклости вниз, 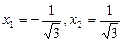 – точки перегиба.
– точки перегиба.
10. Найти наибольшее и наименьшее значения каждой из следующих функций:
а) 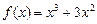 на отрезке
на отрезке  ; б)
; б)  на отрезке
на отрезке  .
.
Ответ: а)  – наибольшее значение,
– наибольшее значение,  – наименьшее значение; б)
– наименьшее значение; б)  – наибольшее значение,
– наибольшее значение,  – наименьшее значение.
– наименьшее значение.






