ВВЕДЕНИЕ
Данные методические указания содержат тематический план курса «Математика», задачи для самостоятельного решения, вопросы для подготовки к компьютерному тестированию, список учебной литературы.
Тематический план курса
| № п/п | Наименование раздела, темы | |
| 1. | РАЗДЕЛ I. «Элементы линейной алгебры и аналитической геометрии» | |
| 1.1 | Матрицы и операции над матрицами | |
| 1.2 | Определители. Свойства определителей | |
| 1.3 | Обратная матрица. Ранг матрицы | |
| 1.4 | Системы m линейных уравнений с n неизвестными | |
| 1.5 | Векторы. Линейные и нелинейные операции над векторами | |
| 1.6 | N-мерный вектор и векторное пространство | |
| 1.7 | Линии и их уравнения на плоскости. Прямая линия | |
| 1.8 | Плоскость и прямая в пространстве | |
| 1.9 | Кривые линии второго порядка | |
| 1.10 | Поверхности второго порядка | |
| 2. | РАЗДЕЛ II. «Математический анализ: функция одной переменной» | |
| 2.1 | Предел числовой последовательности | |
| 2.2 | Функции, предел функции | |
| 2.3 | Непрерывность функции | |
| Аудиторная контрольная работа по разделу II | ||
| 3. | РАЗДЕЛ III. «Дифференциальное исчисление» | |
| 3.1 | Производная и дифференциал функции | |
| 3.2 | Монотонность и экстремум функции | |
| 3.3 | Комплексное исследование функции | |
| 3.4 | Кривизна плоской линии | |
| 4. | РАЗДЕЛ IV. «Функции нескольких переменных» | |
| 4.1 | Функция нескольких переменных: базисные понятия | |
| 4.2 | Частные производные и дифференциал функции нескольких переменных | |
| 4.3 | Экстремум функции двух переменных | |
| 4.4 | Условный экстремум функции двух переменных | |
| 4.5 | Градиент и производная по направлению | |
| Аудиторная контрольная работа по разделу IV | ||
| 5. | РАЗДЕЛ V. «Интегральное исчисление» | |
| 5.1 | Первообразная функции и неопределенный интеграл | |
| 5.2 | Основные методы интегрирования неопределенных интегралов (метод подстановки, метод интегрирования по частям, интегрирование выражений содержащих квадратный трехчлен) | |
| 5.3 | Интегрирование рациональных функций | |
| 5.4 | Интегрирование тригонометрических и иррациональных функций | |
| 5.5 | Определенный интеграл | |
| 5.6 | Применение определенного интеграла | |
| 5.7 | Несобственные интегралы |
РАЗДЕЛ I ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
Вопросы для подготовки к тестированию:
1. Что называется матрицей?
2. Каковы виды матриц?
3. Сформулируйте определение операции сложения, разности, умножения матриц, возведения в степень и умножения на число. Какие матрицы можно перемножать?
4. Что называется определителем 1-го 2-го и 3-го порядков?
5. Что называется минором и алгебраическим дополнением?
6. Сформулируйте определение определителя n -го порядка.
7. Сформулируйте основные свойства определителей?
8. Каковы способы вычисления определителей?
9. Что называется обратной матрицей?
10. Сформулируйте теорему о единственности матрицы обратной данной?
11. Опишите алгоритм нахождения матрицы обратной данной?
12. Что называется рангом матрицы?
13. Какие из элементарных преобразований матрицы сохраняют ранг матрицы?
14. Опишите алгоритм нахождения ранга матрицы методом окаймления.
15. Что называется вектором, длиной вектора, единичным вектором, нулевым вектором?
16. Как найти длину вектора?
17. Как найти расстояние между двумя точками?
18. Какие векторы называются коллинеарными? компланарными?
19. Какие операции над векторами называются линейными?
20. Как определяются эти операции и каковы их свойства?
21. Выведите формулы деления отрезка в данном отношении.
22. Как найти координаты середин отрезка?
23. Что называется скалярным произведением двух векторов, каковы его свойства и как оно выражается через координаты векторов?
24. Запишите формулу угла между векторами.
25. Сформулируйте условие перпендикулярности двух векторов?
26. Что называется векторным произведением двух векторов, каковы его свойства и как оно выражается через координаты векторов?
27. Что называется смешанным произведением трех векторов, каковы его свойства и как оно выражается через координаты векторов?
28. Что называется системой m линейных уравнений c n неизвестными?
29. Какая система уравнений называется совместной (несовместной), определенной (неопределенной), равносильной?
30. В чем сущность матричного способа решения системы линейных уравнений (метод обратной матрицы).
31. Напишите формулы Крамера. В каком случае они применимы?
32. В чем сущность метода Гаусса для решения системы линейных уравнений?
33. Что называется однородной системой уравнений?
34. Сформулируйте теорему Кронекера-Капелли.
35. Что называется уравнением линии на плоскости?
36. Что называется направляющим ветором прямой?
37. Что называется нормальным вектором прямой?
38. Как записывается общее уравнение прямой?
39. Как записывается уравнение прямой с угловым коэффициентом?
40. Как записывается векторное уравнение прямой?
41. Как записывается каноническое уравнение прямой?
42. Как записывается параметрическое уравнение прямой?
43. Как записывается уравнение прямой проходящей через данную точку, уравнение пучка прямых?
44. Как записывается уравнение прямой проходящей через две точки?
45. Напишите формулу угла между прямыми.
46. Напишите формулу расстояния от точки до прямой.
47. Сформулируйте условия пересечения, параллельности и перпендикулярности прямых.
48. Как записывается общее уравнение плоскости?
49. Напишите уравнение плоскости, проходящей через три точки.
50. По какой формуле можно рассчитать угол между двумя плоскостями?
51. Напишите виды уравнений прямой в пространстве.
52. Сформулируйте условия параллельности и перпендикулярности прямой и плоскости.
53. По какой формуле можно рассчитать угол между прямой и плоскостью?
54. Сформулируйте определение окружности, эллипса, гиперболы и параболы, запишите их уравнения.
Задачи для подготовки к тестированию:
1. Вычислить матрицу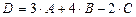 
, если 
, 
, 
.
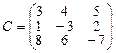Ответ: 
.
2. Вычислить матрицу 
, если
.
Ответ: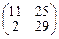 
.
3. Вычислить определители третьего порядка: а) 
; б) 
.
4. Определить, имеет ли матрица А обратную, и если имеет, то вычислить ее:
Ответ: 
.
5. Найти скалярное произведение векторов 
и 
, если:
а) 
, 
; б) 
, 
.
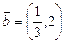Ответ: а) 0; б) 2.
6. Даны два вектора 
и 
. Найти их скалярное произведение и угол между ними. Чему равно выражение 
.
Ответ: (4; 4/9; 47)
7. Найти векторное произведение векторов: 
, 
; 
.
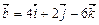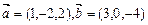Ответ: (8; 32; 16); (8; 10; 6).
8. Решить системы уравнений методом обратной матрицы.
а) 
б) 
Ответ: а) (2; 3; –1); б) (2; –1; –2)
9. Решить системы уравнений методом Крамера.
а) 
б) 
Ответ: а) (1; –2; –3); б) (2; 4; 5).
10. Решить системы уравнений методом Гаусса.
а) 
б) 
Ответ:а)(3; –2; –2); б) (1; 2; 2; 0)
11. Даны вершины треугольника 
. Составить уравнение медианы, проведенной из вершины С.
Ответ: 
11. Составить уравнение сторон треугольника, вершинами которого являются точки 
.
Ответ: 
.
12. Даны координаты вершин треугольника АВС: 
. Составить уравнение высоты СК.
Ответ: 
.
