Рассмотрим определители для матриц первого, второго и третьего порядков:
а) Пусть А= (а11), тогда 
(1)
Из формулы (1) следует, что определитель для матрицы первого порядка совпадает с элементом матрицы 
б) Пусть 
,тогда 
(2)
Из формулы (2) следует, что определитель для матрицы второго порядка равен разности произведений элементов матрицы, стоящих на главной и побочной диагоналях.
в.) Пусть 
, тогда 
(3)
Формулу (3) запомнить значительно труднее, чем (1) и (2), но это и не требуется, так как существуют различные правила,позволяющие легко подсчитать те шесть слагаемых, из которых состоит определитель для матрицы третьего порядка.
Например, можно использовать «правило треугольников», которое условно показано на схемах 1 и 2.
схема 1 схема 2
Первые три слагаемые, входящие в формулу (3) со своим знаком, подсчитываются в соответствии со схемой 1, а следующие три слагаемые, входящие с противоположным знаком, подсчитываются по схеме 2.
10) Алгебраическим дополнением элемента аij квадратной матрицы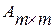 
называется число Аij,вычисляемое по формуле:
где Mij -определитель полученный из определителя матрицы 
удалением строки с номером i и столбца с номером j.
11)Обратная матрица
Матрица А-1 называется обратной к матрице А, если
,где Е - единичная матрица. Из определения следует, что матрицы А и А-1 - квадратные матрицы одного порядка. Квадратная матрица имеет обратную, если ее определитель отличен от нуля и 
, где Аij -алгебраические дополнения элемента аij матрицы .
12) Решение простейших алгебраических уравнений
а) 
, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой 
.Тогда 
.
б) 
, где А и В - заданные матрицы, причем А - квадратная матрица, определитель которой .Тогда 
Примеры:
1) Выполнить действия: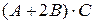 
, где
Решение: 
(по п. 6)
(по п.7)
(по п.8)
2) Найти А-1,если 
Решение:
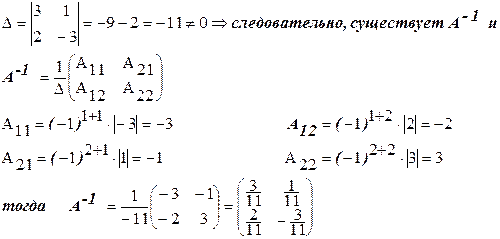
Проверим, верно ли нашли А-1 . Для этого умножим А на А-1 и убедимся, что получим единичную матрицу.
Задача 1.
Решить уравнение AX - B = C, где
Задача 2
2.1-2.20. Даны координаты точек А, В, С. Найти уравнения сторон треугольника АВС. Найти уравнение одной из медиан треугольника АВС. Найти уравнение одной из высот треугольника АВС. Найти уравнение одной из биссектрис треугольника АВС. Найти площадь треугольника АВС.
| Вариант | А | В | С | Вариант | А | В | С |
| 2.1 | (1;2) | (2;0) | (-1;1) | 2.11 1 | (1;3) | (3;0) | (-1;1) |
| 2.2 | (2;1) | (1;0) | (-1;2) | 2.12 1 | (3;1) | (1;0) | (-1;3) |
| 2.3 | (2;0) | (1;1) | (-1;2) | 2.13 1 | (3;0) | (1;1) | (-1;3) |
| 2.4 | (2;1) | (1;0) | (1;-1) | 2.14 1 | (3;-1) | (1;0) | (1;1) |
| 2.5 | (-1;0) | (2;1) | (1;-1) | 2.15 1 | (-1;0) | (3;1) | (1;-1) |
| 2.6 | (1;-1) | (-1;0) | (2;1) | 2.16 1 | (1;-1) | (-1;0) | (3;1) |
| 2.7 | (1;-2) | (0;1) | (2;-1) | 2.17 1 | (1;-3) | (0;1) | (3;-1) |
| 2.8 | (2;-1) | (1;-2) | (0;1) | 2.18 1 | (3;-1) | (1;-3) | (0;1) |
| 2.9 | (-2;1) | (-1;-2) | (1;2) | 2.19 1 | (-3;1) | (-1;-3) | (1;3) |
| 2.10 | (2;2) | (-2;1) | (1;1) | 2.20 1 | (-3;3) | (3;1) | (1;1) |
