1. Высшая математика для экономических специальностей. Учебник и Практикум (части I и II) / Под ред. Н.Ш. Кремера. М.: Высшее образование, 2008
2. Теория вероятностей и математическая статистика. Н.Ш. Кремер. М.: ЮНИТИ, 2007.
3. Математика. Математический анализ. Теория вероятностей и математическая статистика. Под ред. А.Н. Данчула. М.: Издательство РАГС, 2005.
4. Сборник задач по математике. /А.Н. Данчул (отв.ред) / М.: Издательство РАГС, 2005.
КОНТРОЛЬНЫЕ ЗАДАНИЯ
Выполняются два контрольных задания по 6 задач в каждом. По выданному преподавателем номеру варианта задания с помощью таблицы вариантов, приведенной на следующей странице, определяются номера варианты входящих в задание задач. Образец оформления титульного листа задания приведен в Приложении.
Сроки сдачи заданий:
· задание 1 – 10 неделя (до 8 апреля);
· задание 2 – 16 неделя (до 15 мая).
Сроки зачета заданий (с учетом исправления ошибок):
· задание 1 – 11 неделя (до 15 апреля);
· задание 2 – 17 неделя (до 22 мая).
Таблица вариантов
| Задача | ||||||
| № варианта задания | Номера вариантов задач | |||||
| 1. | ||||||
| 2. | ||||||
| 3. | ||||||
| 4. | ||||||
| 5. | ||||||
| 6. | ||||||
| 7. | ||||||
| 8. | ||||||
| 9. | ||||||
| 10. | ||||||
| 11. | ||||||
| 12. | ||||||
| 13. | ||||||
| 14. | ||||||
| 15. | ||||||
| 16. | ||||||
| 17. | ||||||
| 18. | ||||||
| 19. | ||||||
| 20. | ||||||
| 21. | ||||||
| 22. | ||||||
| 23. | ||||||
| 24. | ||||||
| 25. | ||||||
| 26. | ||||||
| 27. | ||||||
| 28. | ||||||
| 29. | ||||||
| 30. | ||||||
| 31. | ||||||
| 32. |
Контрольное задание №1
Задача 1. Исследовать сходимость числового ряда
Вариант 1
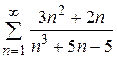
| Вариант 6

|
Вариант 2

| Вариант 7

|
Вариант 3

| Вариант 8

|
Вариант 4

| Вариант 9

|
Вариант 5

| Вариант 10

|
Задача 2. Разложить функции в ряд Маклорена и найти радиус сходимости ряда
Вариант 1

| Вариант 6

|
Вариант 2

| Вариант 7

|
Вариант 3

| Вариант 8

|
Вариант 4

| Вариант 9

|
Вариант 5

| Вариант 10

|
Задача 3. Исследовать функции на экстремум
Вариант 1

| Вариант 6

|
Вариант 2

| Вариант 7
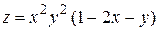
|
Вариант 3

| Вариант 8

|
Вариант 4

| Вариант 9
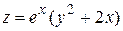
|
Вариант 5

| Вариант 10

|
Задача 4. Вычислить двойные интегралы  по заданной области
по заданной области 
Вариант 1

| Вариант 6

|
Вариант 2

| Вариант 7

|
Вариант 3

| Вариант 8

|
Вариант 4

| Вариант 9

|
Вариант 5

| Вариант 10
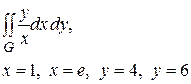
|
Задача 5. Найти общее решение дифференциального уравнения первого порядка
Вариант 1
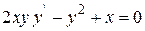
| Вариант 6

|
Вариант 2

| Вариант 7
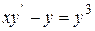
|
Вариант 3

| Вариант 8

|
Вариант 4

| Вариант 9

|
Вариант 5
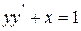
| Вариант 10

|
Задача 6. Найти общее решение неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами.
Вариант 1

| Вариант 6

|
Вариант 2

| Вариант 7

|
Вариант 3

| Вариант 8

|
Вариант 4

| Вариант 9

|
Вариант 5

| Вариант 10

|
Контрольное задание №2
Задача 1. Бросают два кубика. Суммируют число очков, выпавших на верхних гранях кубиков. Построить множество элементарных событий W и его подмножество, соответствующее указанному событию А. Найти вероятность события А. Построить подмножество, соответствующее событию  (дополнение А). Найти его вероятность.
(дополнение А). Найти его вероятность.
| Вариант | Событие А |
| А={сумма очков больше 3} | |
| А={сумма очков больше 4} | |
| А={сумма очков больше 5} | |
| А={сумма очков больше 6} | |
| А={сумма очков больше 7} | |
| А={сумма очков больше 8} | |
| А={сумма очков больше 9} | |
| А={сумма очков больше 10} | |
| А={сумма очков больше 2} |
Задача 2. В одном сосуде находятся Б1 белых и Ч1 черных шаров. Во втором – Б2 белых и Ч2 черных. Бросают два кубика. Если сумма очков, выпавших на верхних гранях, меньше 10, берут шар из первого сосуда, если больше или равна 10 – из второго.
| Вариант | Условие задачи | |
| Б1=7; Ч1=6; Б2=5; Ч2=9 | Вынут белый шар. Какова вероятность того, что сумма очков была не меньше 10? | |
| Б1=7; Ч1=6; Б2=5; Ч2=9 | Вынут черный шар. Какова вероятность того, что сумма очков была меньше 10? | |
| Б1=6; Ч1=5; Б2=7; Ч2=9 | Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10? | |
| Б1=7; Ч1=5; Б2=9; Ч2=6 | Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10? | |
| Б1=5; Ч1=6; Б2=9; Ч2=6 | Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10? | |
| Б1=5; Ч1=9; Б2=7; Ч2=6 | Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10? | |
| Б1=5; Ч1=7; Б2=6; Ч2=9 | Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10? | |
| Б1=5; Ч1=7; Б2=9; Ч2=6 | Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10? | |
| Б1=4; Ч1=8; Б2=9; Ч2=6 | Вынут белый шар. Какова вероятность того, что сумма очков была меньше 10? | |
| Б1=8; Ч1=4; Б2=6; Ч2=9 | Вынут черный шар. Какова вероятность того, что сумма очков была не меньше 10? |
Задача 3. Случайная величина X задана плотностью распределения вероятностей (см. график). Построить график функции распределения вероятностей, найти математическое ожидание и дисперсию случайной величины.

| Вариант | a | b | c | d | Вариант | a | b | c | d |
| 0.3 | 1.15 | 0.5 | 1.7 | 2.28 | 0.6 | ||||
| 0.6 | 1.3 | 0.5 | 2.6 | 0.4 | |||||
| 0.5 | 1.25 | 0.5 | 2.5 | 3.3 | 0.4 | ||||
| 0.5 | 1.7 | 0.6 | 3.6 | 0.4 | |||||
| 1.5 | 2.2 | 0.6 | 4.4 | 0.6 |






