Числовые характеристики выборки.
Целью работы являлосьдля заданной выборки вычислить выборочное среднее, выборочную дисперсию, вычислить доверительный интервал для математического ожидания случайной величины, построить гистограмму выборки, проверить закон распределения выборки методом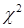 
Пирсона.
В первый столбец таблицы Excel разместим данные выборки, содержащиеся в файле 1.txt. Объем выборки 200. В строке ниже высчитываем сумму элементов выборки: Sx=-2242,6135
Далее вычисляем выборочное среднее по формуле:
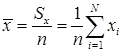= 11,2130675
Во втором столбце таблицы Excel размещаем значения, равные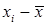 
, т.е. отклонения от среднего значения. В строке ниже под вторым столбцом вычисляем сумму значений: сумма равна 1,95399E-14, т.е сумму отклонений всех значений выборки от среднего значения. Эта величина должна быть близка к нулю.
В третьем столбце размещаем квадраты значений второго столбца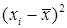 
В строке ниже размещаем сумму элементов третьего столбца:
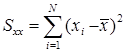= 23218,94309
В следующей строке третьего столбца - эту сумму, деленную на объем выборки – дисперсия выборки:
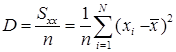= 116,0947155
Исправленная дисперсия вычисляется по формуле:
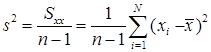=116,678106
Среднее квадратическое отклонение выборки:
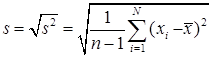=10,80176402
Результаты оформляем в виде таблицы
| Явная формула | Значение по явной формуле | Имя функции Excel | Значение Функции Excel | |
| Выборочное среднее |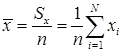
| 11,2130675 | СРЗНАЧ | 11,2130675 |
| дисперсия |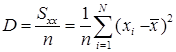
| 116,0947155 | ДИСПР | 116,0947155 |
| Исправленная дисперсия |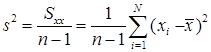
| 116,678106 | ДИСП | 116,678106 |
| Среднее квадратическое отклонение |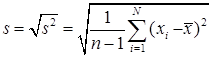
| 10,80176402 | СТАНДОТКЛОНА | 10,80176402 |
Строим точечную диаграмму выборки и проверяем соответствие числовых характеристик выборки данным на диаграмме.
Вычислить доверительный интервал для математического ожидания случайной величины с надежностью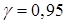 
.
Границы доверительного интервала определяются по формулам
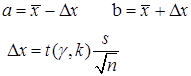
Где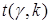 
- квантиль распределения Стьюдента с числом степеней свободы k=n-1. Вычисляется в Excel с помощью статистической функции 
.
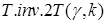| 1,971957 - коэффициент Стьюдента |
| 1,506181- ∆Х |
| a= 9,706887 b=12,71925 |
Проверка закона распределения случайной величины методом Пирсона.
В новом столбце вычисляем максимальный элемент выборки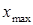 
= 54,6252, минимальный элемент 
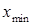=0,0344. Шаг разбиения диапазона значений выборки для построения гистограммы
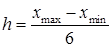= 9,098466667
В следующем столбце размещаем значения, являющиеся внутренними границами интервалов: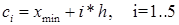 
| c1 | 
| ||||
| с2 | 
| ||||
| c3 |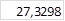 
| ||||
| c4 |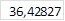 
| ||||
| c5 |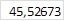 
| ||||
В следующих столбцах размещаем массив частот для гистограммы
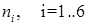
и относительных частот:
| n1 | |
| n2 | |
| n3 | |
| n4 | |
| n5 | |
| n6 |
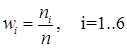
| w1 | 0,55 |
| w2 | 0,25 |
| w3 | 0,1 |
| w4 | 0,065 |
| w5 | 0,02 |
| w6 | 0,015 |
Представляем гистотрамму графически:
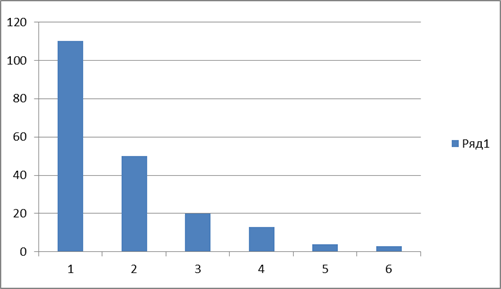
Вычислить теоретические частоты, соответствующие равномерному
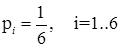
и нормальному распределению
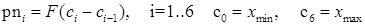
| pn1 | 0,273285 |
| pn2 | 0,318424 |
| pn3 | 0,190089 |
| pn4 | 0,058055 |
| pn5 | 0,009044 |
| pn6 | 0,000716 |
Вычислить критерий Пирсона соответствия выборке равномерному:
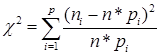= 255,82
и нормальному распределению:
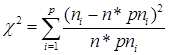= 127,3615
Вывод о законе распределения выборки:
Выбор интервалов – не простая задача при практическом использовании критерия хи-квадрат. Следует иметь в виду, что преобразование выборки к интервальному виду (в случае непрерывной Х) связано с некоторой потерей информации. Однако для эффективной работы критерия Пирсона группировка является необходимой операцией, позволяющей параметризировать критерий. Но при этом число интервалов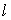 
не должно быть ни слишком малым, иначе будет потерянно слишком много информации о распределении генеральной совокупности, ни слишком большим, т.к. в этом случае получаются слабо наполненные разряды, и мощность критерия падает. Теоретически этот вопрос исследовался в специальной литературе, где было показано, что при проверке на нормальность оптимальное число интервалов группировки определятся соотношением
