Часть 1. Математика.
1. Понятие множества; элементы множества; мощность множества; отношения принадлежности и включения. Виды множеств.
2. Числовые множества.
3. Операции над множествами, их свойства.
4. Соответствия между элементами множеств, их виды (в т.ч. отображения и биекция).
5. Понятие графа. Виды графов, их применение.
6. Понятие о комбинаторной задаче. Правила суммы и произведения.
7. Перестановки из 
элементов.
8. Упорядоченные подмножества из элементов по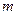 
. Размещения. Количество размещений.
9. Подмножества из элементов по 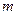. Сочетания. Количество всех подмножеств множества, содержащего элементов.
10. Размещения с повторениями.
11. Сочетания с повторениями, их применение.
12. Случайные события. Достоверные и невозможные события. Испытание, элементарный исход, полная система исходов. Относительная частота и вероятность наблюдаемого события.
13. Совместные и несовместные, зависимые и независимые события. Правила суммы и произведения.
14. Случайные величины. Функция распределения случайных величин. Математическое ожидание.
15. Дисперсия. Закон больших чисел.
16. Высказывания; высказывательные формы; кванторы общности и существования. Область отправления и множество истинности высказывания.
17. Логические операции над высказываниями (логические связки), порядок их выполнения в сложной формуле.
18. Отрицания логических связок.
19. Свойства дизъюнкции и конъюнкции.
20. Свойства импликации и эквивалентности.
21. Функции, их исследование с помощью основ математического анализа.
Часть 2. История математики.
1. Этапы развития науки; роль математики в развитии наук и особенности ее развития.
2. Возникновение основных математических понятий (число, фигура,…).
3. Обозначения чисел и системы счисления у разных народов.
4. Математика в древних Месопотамии и Египте. Математика в древних Китае и Индии.
5. Математика в Древней Греции и Древнем Риме.
6. Математика в Средние Века (Средняя Азия).
7. Математика в древней Руси.
8. Математика средних веков в Западной Европе.
9. Математика Эпохи Возрождения.
10. Математика Западной Европы в XVII веке.
11. Математика в России в XIV-XVII в. (влияние татаро-монгольского ига и отношений с Западной Европой).
12. Развитие математики в XVIII веке в Западной Европе.
13. То же – в России.
14. Возникновение дифференциального и интегрального исчислений; их развитие.
15. Геометрия – XIX век.
16. 23 проблемы, поставленные Гильбертом, их решение.
17. Основные ветви математики, их зарождение и роль в настоящее время (алгебра, теория чисел, теория вероятностей, тригонометрия,…).
18. Кибернетика и информатика.
19. Основания математики и математическая логика.
20. Основные черты современной математики и пути ее развития.
Сентябрь 2011 года Н.А.Попова Н.А Антонова
*) Здесь и далее имя ученого означает, что требуется изложить сведения о его жизни и его вкладе в историю развития математики.
