Кафедра математики и информационных систем в образовании
Методические указания по курсу “Математика”
Для студентов I курса института гуманитарных наук
(заочное отделение)
Преподаватель Антонова Н.А.
Сыктывкар 2011
Учебный план по курсу “Математика”
для I курса института гуманитарных наук (заочное отделение)
На 2011-12 уч.год преподавателя Антоновой Н.А.
I семестр. Лекции (4 часа)
1. Краткий исторический очерк развития математики. Обзор литературы.
2. Множества, элементы комбинаторики, введение в теорию вероятностей и математическую логику, знакомство с графами.
Консультация (2 час). Методические указания к выполнению контрольной работы.
Задания для самостоятельной работы:
1. Контрольная работа (5 задач. См. приложение 1).
2. Подготовка (написание) реферата по выбранной теме (список тем – приложение 2).
II семестр. Практические занятия (4 часа). Решение задач.
1. Множества. Элементы комбинаторики.
2. Элементы теории графов и математической логики.
3. Элементы теории вероятностей. Математическое ожидание и дисперсия, их применение в математической статистике.
4. Функции и их графики.
Консультации (к зачету).
Зачет ставится с учетом оценок за:
1) контрольную работу,
2) реферат (по индивидуальной теме),
3) ответы на вопросы зачета.
Список основной литературы:
1. Столл Р.Р. Множества. Логика. Аксиоматические теории. М. Просв., 1968. 230 с.
2. Колмогоров А.Н., Журбенко И.Т., Прохоров А.В. Введение в теорию вероятностей. М. Физматгиз, 1982.
3. Мендельсон Э. Введение в математическую логику. М. Наука, 1984. 320 с.
4. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. Учебное пособие. М. Наука, 1989. 576 с.
5. Стройк Д.Я. Краткий очерк истории математики. М. Наука, 1978. 336 с.
6. Мациевский С.В. Высшая математика для гуманитариев: учебное пособие. –Калининград: Изд-во РГУ им. И. Канта, 2010.— 299 с.: ил., табл.
7. Гресс П.В. Математика для гуманитариев: учебное пособие. –М: Юрайт, 2000.— 112 с.
8. Матвеев И.В. Функции и их графики. М. МГУ, 1970. 104 с.
9. Гнеденко Б.В., Хинчин А.Я. Введение в теорию вероятностей. М. Физматгиз, 1982. 160 с.
10. Стройк Д.Я. Краткий очерк истории математики. М. Наука, 1978. 336 с.
11. Рыбников К.А. Возникновение и развитие математической науки. Пособие для учителя. М. Просвещение, 1987. 159 с.
Приложение 1.
Контрольная работа по математике
для I курса гуманитарного института СГУ (заочное отделение)
Задание 1. (Множества. Комбинаторика.)
1) Составить множества различных букв. А – своего полного имени, В – своего отчества, С – своей фамилии.
2) Найти объединение и пересечение множеств А и В.
3) Найти дополнения к С до А и к А до С.
4) Проверить на диаграммах, верно ли равенство:  .
.
5) Вычислить, сколько элементов имеет декартово произведение множеств А и В, изобразить их точками плоскости.
6) Сколько различных аббревиатур можно составить из всех букв множества С? В каждой из аббревиатур использовать каждую букву из множества С только по одному разу (т.е. без повторений).
7) Сколько различных трехбуквенных слов можно составить из букв множества В, если слова составляются из разных букв (без повторений)? Что собой представляют наборы букв этих слов – сочетания или размещения?
8) Сколько различных подмножеств (всех) имеет множество А?
Пример решения такой задачи. Пусть автор – Пафнутий Львович Чебышёв (будем считать е и ё за одну и ту же букву). Тогда
1) А={П, А, Ф, Н, У, Т, И, Й}, В={Л, Ь, В, О, И, Ч}, С={Ч, Е, Б, Ы, Ш, В}.
2)  = {П, А, Ф, Н, У, Т, И, Й, Л, Ь, В, О, Ч}.
= {П, А, Ф, Н, У, Т, И, Й, Л, Ь, В, О, Ч}.  ={И}.
={И}.
3) Т.к.  Æ, то
Æ, то  и
и  .
.
4)  {П, А, Ф, Н, У, Т, И, Й, В, Ч}.
{П, А, Ф, Н, У, Т, И, Й, В, Ч}.
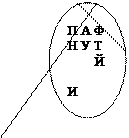 |








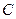









 | |||
 | |||









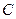


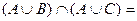 {П, А, Ф, Н, У, Т, И, Й, В, Ч}.
{П, А, Ф, Н, У, Т, И, Й, В, Ч}.
Ответ: Т.к. получилось одно и то же множество, то равенство верно.








 5)
5) 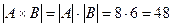 . Ч
. Ч
И
 О
О
 В
В
 Ь
Ь

 Л
Л


П А Ф Н У Т И Й
6) Так как аббревиатуры составляются из всех букв множества С и без повторений, то их количество равно множеству порядков на множестве С:  .
.
7) Т.к. при перестановке букв в слове получаются другие (новые) слова (например, ЛОВ и ВОЛ), то наборы букв для слов – это размещения, т.к. важен порядок выбора букв. Всех размещений из букв множества В по 3 - 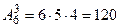 . Но нет слов, начинающихся с буквы “ь”, поэтому такие наборы надо исключить, их количество равно
. Но нет слов, начинающихся с буквы “ь”, поэтому такие наборы надо исключить, их количество равно  . Тогда различных трехбуквенных слов
. Тогда различных трехбуквенных слов  .
.
Ответ: 100.
8) Т.к.  , то количество подмножеств -
, то количество подмножеств -  .
.
Задание 2 (Графы)
Пусть множество А из предыдущего задания есть множество обозначений вершин для построения графов, т.е. множества точек V.
1)  Изобразить вершины графа точками, обозначить их и соединить ребрами так, чтобы получился а) полный граф -
Изобразить вершины графа точками, обозначить их и соединить ребрами так, чтобы получился а) полный граф -  , б) двудольный граф -
, б) двудольный граф - 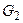 , в) полный двудольный граф -
, в) полный двудольный граф - 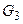 , г) регулярный граф -
, г) регулярный граф -  (указать его степень), д) односвязный граф с одним “мостом” -
(указать его степень), д) односвязный граф с одним “мостом” -  , е) непростой граф -
, е) непростой граф -  (т.е выполнить не менее шести рисунков).
(т.е выполнить не менее шести рисунков).
2) Найти среди изображенных графов а) эйлеров граф, б) полуэйлеров граф, в) граф, имеющий циклы (если они есть на рисунках, подписать их; если нет, то изобразить такие графы).
3) Из множеств А, В и С предыдущей задачи выбрать множество с наименьшим числом букв (элементов) и, считая их вершинами графа, изобразить все возможные деревья с вершинами во всех этих точках.
Например.



 b
b






a c полный граф с пятью вершинами; он же регулярный
 (однородный), степень вершин r = 4; а также он эйлеров;
(однородный), степень вершин r = 4; а также он эйлеров;
l d односвязный.
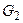 n двудольный и двусвязный граф; (двудольный -
n двудольный и двусвязный граф; (двудольный -

 m неполный).
m неполный).
l

 k o
k o

 p q
p q
s



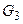 t u непростой, односвязный с одним “мостом”,
t u непростой, односвязный с одним “мостом”,

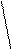

 полуэйлеров граф.
полуэйлеров граф.
xv


 z w
z w
y
Задание 3 (Теория вероятностей)
Возьмем множества А и В из задания 1. Пусть каждая из букв написана на отдельной карточке и множества А и В – это две колоды карточек (все карточки положены буквами вниз, их не видно).
Вычислить вероятность того, что при выборе наугад по одной карточке из каждой колоды будут вынуты а) 2 одинаковые буквы; б) 2 разные буквы; в) хотя бы одна из букв такая, какую Вы задумали заранее (укажите, какую именно; если есть разные варианты решения, то покажите все решения).
Например,) А={П, А, Ф, Н, У, Т, И, Й}, В={Л, Ь, В, О, В, И, Ч}. Тогда: а) общая буква только одна – И; вероятность ее выбора из А равна  , вероятность ее выбора из В равна
, вероятность ее выбора из В равна  ; вероятность ее выбора из А и из В –
; вероятность ее выбора из А и из В –  (правило произведения); б) т.к. во всех остальных случаях буквы будут различны, то вероятность выбора двух разных букв равна
(правило произведения); б) т.к. во всех остальных случаях буквы будут различны, то вероятность выбора двух разных букв равна  (можно ее найти и другим способом); в) если задумана буква “И”, то вероятность ее выбора хотя бы из одной колоды – это 3 случая: “И” из А и любая другая буква из В, “И” из В и любая другая буква из А, а также “И” – из А и В; сложив вероятности, получим:
(можно ее найти и другим способом); в) если задумана буква “И”, то вероятность ее выбора хотя бы из одной колоды – это 3 случая: “И” из А и любая другая буква из В, “И” из В и любая другая буква из А, а также “И” – из А и В; сложив вероятности, получим:  . Аналогично для других букв (2 случ.).
. Аналогично для других букв (2 случ.).
Внимание! В заданиях 4 и 5 каждый студент должен выполнить свой вариант. Номер варианта соответствует Вашему номеру зачетной книжки следующим образом: а) если две последние цифры номера зачетной книжки составляют число не больше тридцати, то это и есть номер Вашего варианта; б) если две последние цифры составляют число большее тридцати, то из него следует вычесть 30 столько раз, сколько возможно; остаток и есть номер Вашего варианта; если две последние цифры номера зачетной книжки 60 ли 90, то Вы выполняете вариант 30. Например, номер зачетной книжки …41 – вариант 11, т.к. 41=30+11, …62 – вариант 2, …97 – вариант 7; …208 – т.е. …08 – вариант 8.
Задание 4 (Математическая логика).
А. В вариантах 1 – 15 составить таблицу истинности формулы:
1. ù x & y Ú (ù y º x Ú ù y); 2. ù (x &ù y)Ú (ù x & y) º ù y);
3. y Ú ù x & (y & x ® ù x); 4. x Ú y º (ù x & ù y ® y);
5. x º (x Ú ù y ® ù y & ù x); 6. (y ® ù x Ú (x & y)) º x Ú y;
7. ù (x Ú ù y) ® (x Ú ù y); 8. x Ú (y ® y Ú ù (x Ú y));
9. x Ú y ® ù y & (x ® y); 10. x & (ù y ® x Ú y);
11. x º (y ® ù x Ú (x º ù y)); 12. (x Ú y) ® (y & ù x);
13. (x ® y) ® (ù x & ù (y Ú x)); 14. x º (ù y ® x) Ú (x ® ù y));
15. (x Ú ù y) & (ù x Ú y) º ù y;
Б. В вариантах 16-30 проверить, является ли формула тавтологией:
16. (y ® (x Ú ù y)) & (x ® (y Ú ù x)); 17. (x Ú y)® (y Ú ù x);
18. x º (x Ú ù y) & ù y); 19. x ® (x Ú (ù y & x));
20. x ® ((y & ù x) ® x); 21. (x ® y) ® x Ú y º ù (ù x & ù y);
22. x Ú y º ù (ù x & ù y); 23. (ù x Ú y ® y) º x Ú y;
24. (ù x Ú y ® x) º x & y; 25. ù (x ® y) Ú (ù y ® ù x);
26. ù (x ® y) & ù (y ® ù x); 27. x & ù y ® (x Ú y º ù x);
28. x Ú ù y ® (ù y & ù x)º ù x; 29. x º (y ® x & ù y);
30. ù x º (y Ú (x ® ù y)).
Примеры. А. Составить таблицу истинности формулы
(x ® ù y) & (x Ú y)) º x Ú ù y.
Решение. Порядок выполнения действий:
x ® t

 Ú
Ú

 & z º
& z º

 y ù Ú v
y ù Ú v
| x | y | ù y | x Ú y | z ù y & (x Ú y) | T (x ® z) | v (x Ú ù y) | Ответ: t º v |
| И И Л Л | И Л И Л | Л И Л И | И И И Л | Л И Л Л | Л И И И | И И Л И | Л И Л И |
Б. Проверить, является ли формула (x ® ù y) & (x Ú y)) º (x ® ù y) тавтологией.
Решение (аналогично решению предыдущей задачи, отличается лишь v: x ® ù y.
| x | y | ù y | x Ú y | z ù y & (x Ú y) | T x ® z | v x ® ù y | Ответ: t º v |
| И И Л Л | И Л И Л | Л И Л И | И И И Л | Л И Л Л | Л И И И | Л И И И | И И И И |
Ответ: да, тавтология.
Задание 5.
Построить график дробно-рациональной функции  (варианты 1-30), предварительно исследовав ее по следующему плану:
(варианты 1-30), предварительно исследовав ее по следующему плану:
1) найти область определения функции 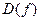 (для этого можно преобразовать формулу, разложив числитель и знаменатель на множители);
(для этого можно преобразовать формулу, разложив числитель и знаменатель на множители);
2) если есть точки разрыва, то выяснить, есть ли в них вертикальные асимптоты (для этого найти в этих точках пределы функции слева и справа);
3) найти наклонные или горизонтальные асимптоты (для этого преобразовать формулу функции, выделив целую часть из дроби);
4) проверить, не обладает ли функция частными свойствами: а) четностью или нечетностью, б) периодичностью (если нет, то доказать, пояснить это);
5) найти точки пересечения графика с осями координат и интервалы знакопостоянства, если точки пересечения с осью  легко находятся;
легко находятся;
6) найти производную и критические точки;
7) по знаку производной выяснить интервалы возрастания и убывания функции и что она имеет в критических точках;
8) изобразить систему координат (в соответствии с исследованными свойствами) и отметить в ней все найденные точки, изобразить асимптоты; для уточнения вида графика найти координаты нескольких дополнительных точек; отметить их и нарисовать график;
9) если в п.5 не были найдены точки пересечения графика с осью  (нули функции), то найти их теперь по графику;
(нули функции), то найти их теперь по графику;
10) найти область изменения функции (по графику и исследованным свойствам).
Варианты: 
1)  ; 11)
; 11) 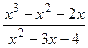 ; 21)
; 21)  ;
;
2)  ; 12)
; 12)  ; 22)
; 22)  ;
;
3) 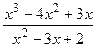 ; 13)
; 13) 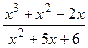 ; 23)
; 23)  ;
;
4)  ; 14)
; 14)  ; 24)
; 24)  ;
;
5) 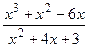 ; 15)
; 15) 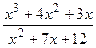 ; 25)
; 25)  ;
;
6)  ; 16)
; 16)  ; 26)
; 26)  ;
;
7) 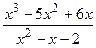 ; 17)
; 17)  ; 27)
; 27)  ;
;
8)  ; 18)
; 18) 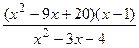 ; 28)
; 28) 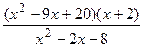 ;
;
9)  ; 19)
; 19)  ; 29)
; 29)  ;
;
10)  ; 20)
; 20)  ; 30)
; 30)  .
.
Пример. Исследовать функцию 
 .
.
Решение. 1) 
 =
=  =
=  при
при  (корни квадратного трехчлена найдены по обратной теореме Виета (в уме)),
(корни квадратного трехчлена найдены по обратной теореме Виета (в уме)),
значит,  .
.
2) а) при  слева
слева  ; (1)
; (1)

| -8 | -7,5 | -7,1 | … |

| -90 | -159,5 | -719,1 | … |
при  справа
справа  ; (2)
; (2)

| -6 | -6,5 | -6,9 | … |

| 121,5 | 681,1 | … |
Значит,  - вертикальная асимптота;
- вертикальная асимптота;
б) при 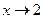 (и слева и справа)
(и слева и справа)  ;
;

| 1,9 | 2,1 |

| 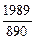
| 
|
асимптоты нет;  - исключенная точка (т. разрыва). (3)
- исключенная точка (т. разрыва). (3)
3) В 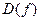



 ; т.к. при
; т.к. при 
 , то
, то
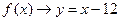 ; таким образом, прямая
; таким образом, прямая  - наклонная асимптота.
- наклонная асимптота.
4) Исследуем на четность: 


 ; видим, что:
; видим, что: 
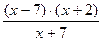 и
и 
 , т.е.
, т.е.  и
и  , значит,
, значит,  общего вида (не обладает ни четностью, ни нечетностью);
общего вида (не обладает ни четностью, ни нечетностью);  не является периодической как дробно-рациональная функция (многочлены – непериодические функции).
не является периодической как дробно-рациональная функция (многочлены – непериодические функции).
5) а) при 
 ; значит,
; значит,
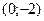 - точка пересечения графика с осью ординат; (4)
- точка пересечения графика с осью ординат; (4)
б) 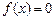 при
при 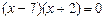 , но
, но  , т.е. при
, т.е. при  или
или  , т.о.
, т.о.
 и
и  - точки пересечения графика
- точки пересечения графика  с осью абсцисс. (5)
с осью абсцисс. (5)
С учетом точек разрыва и найденных значений функции (по (1), (2), (3) и (4), (5)) получаем: при 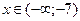
 ; при
; при 
 ;
;
при 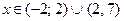
 ; при
; при 
 .
.
6) 
(использована формула:  );
);
а) нет критических точек, где  не существует, т.к.
не существует, т.к.  не имеет значе-
не имеет значе-
ния только при  , но
, но  ;
;
б)  при
при 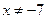 и
и  , т.е. при
, т.е. при  ;
;  ;
;
значит, 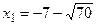 и
и  - критические точки, а
- критические точки, а

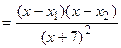 ;
;  .
.
7)

| 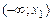
| 
| 
| 
| 
| 
| 
| 
|

| + | - | нет зн. | - | + | + | ||
    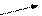 
| 
| 
| нет зн. | 
| ||||
| выводы | от 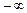 до до 
| max | от  до
до 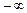
| вертик. асимпт | от 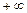 до
до 
| min | от  до
до 
| от  до
до 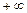
|
Т.к. при 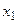 и
и 
 , то преобразуем формулу
, то преобразуем формулу 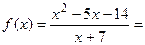
 ; тогда
; тогда
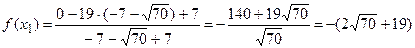 ;
;  ;
;
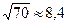 ; поэтому
; поэтому  ,
,  ;
;  ,
,  .
.
8)  ;
;

| -17 | -14 | -12 | -3 | |||

| -36 | -36 | -38 | 2,5 | -2 | 2/3 | 4,5 |
9) см. 5).
10) 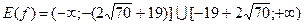 .
.
5 y





 |


 -21 -17 -14 -12 -7 -2 0 7 12 x
-21 -17 -14 -12 -7 -2 0 7 12 x





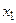

-2

-12
 |
 -36
-36
-38

-40
Приложение 2.
Темы рефератов
1. Возникновение понятия числа; первые системы счисления.
2. Математика в Древнем Египте.
3. Математика в Древней Месопотамии (Шумер, Вавилон, Ассирия).
4. Математика в Древнем Китае.
5. Математика в Древней Греции (1 тысячелетие до н.э.).
6. Пифагор. *)
7. Аристотель.
8. Евклид.
9. Архимед.
10. Математика Древней Греции и Древнего Рима (начало новой эры – I-V века; Александрийская школа).
11. Средневековье. Математика в Индии.
12. Математика в Средней Азии (VIII-XIII века, Улугбек, Омар Хайам и др.).
13. Математика в древней Руси (VIII-XIII века).
14. Математика в эпоху Возрождения (Западная Европа; XII-XV века).
15. Леонардо Пизанский (Фибоначчи). XV век.
16. Леонардо да Винчи. XV век.
17. Франсуа Виет. XVI век.
18. Джон Нэпер (Непер). XVI век.
19. Кардано и Тарталья. XVI век.
20. Коперник, Тихо Браге, Кеплер, Галилей. XVI век.
21. Рене Декарт. XVII век.
22. Блез Паскаль. XVII век.
23. Исаак Ньютон. XVII век.
24. Г.В.Лейбниц. XVII век.
25. Пьер Ферма. XVII век.
26. Даламбер. XVIII век.
27. Леонард Эйлер. XVIII век.
28. Ж.Л.Лагранж. XVIII век.
29. А.М.Лежандр. XVIII век.
30. Г.Монж. XVIII век.
31. П.С.Лаплас. XVIII век.
32. Математика в России XVII-XVIII веков (Роль реформ Петра I; Екатерина II).
33. М.В.Ломоносов.
34. Знаменитые задачи древности (об удвоении куба, о трисекции угла, о спрямлении окружности) и их разрешение (вплоть до XVIII века).
35. К.Ф.Гаусс.
36. Различные доказательства V постулата Евклида (до XIX в. н.э.).
37. Н.И.Лобачевский
38. Основные первоначальные факты геометрии Лобачевского, модели плоскости Лобачевского.
39. Нильс Абель. XIX век.
40. Эварист Галуа. XIX век.
41. Огюстен Коши. XIX век.
42. Карл Вейерштрасс. XIX век.
43. М.В.Остроградский. XIX век.
44. П.Л.Чебышёв. XIX век.
45. С.В.Ковалевская. XIX век.
46. Ф.Клейн. XIX век.
47. А.Пуанкаре. XIX век.
48. Г.Кантор. XIX век.
49. Б.Риман. Конец XIX века.
50. Д. Гильберт. Конец XIX века.
51. Французская математическая школа (XVII-XX в.в.).
52. Немецкая математическая школа (XVII-XX в.в.).
53. Английская математическая школа (XVII-XX в.в.).
54. Российская математическая школа (XVIII-началоXX в.в.).
55. Советская математическая школа.
56. Американская математическая школа (XIX-X X в.в.).
57. Н.Винер.
58. А.Н.Колмогоров.
59. Математика XX века; основные направления развития.
60. Основные стадии развития науки; основные черты современной математики и ее роль в развитии общества.
Примечание. Дополнительная литература к работе над рефератом не указана, т.к. подбор литературы входит как часть в самостоятельную работу студента (этому надо научиться). В пособии Д.Я.Стройка [11] в конце каждой главы есть список рекомендуемой литературы. Можно использовать то, что найдется в Интернете, личной библиотеке или в ближайшей общественной, а также энциклопедические словари.
Приложение 3.
Вопросы к зачету по курсу “Математика”






